在研發大型軍用雷達如空對地雷達,火控雷達,民用氣象雷達等產品過程中經常遇到雷達附近的電磁輻射干擾問題,需要對其周邊的不規則的輻射場進行精確的電磁場強反演還原,以排除其干擾。在通用的計算電磁學方法不能解決問題的情況時,針對這類非對稱特定場景的電磁場分布計算還沒有高效、快速、準確的計算方法的前提下,宇能無線公司提出一種基于改進FDTD和等效計算區域分解的輻射場反演綜合計算電磁方法, 實現某類發射場周圍特定區域任意點的時域近場分布計算、近-遠場電磁變換計算和電磁圖形顯示。該法保障了高效的計算效率和精準的計算精度,同時也有效地減小了計算內存消耗。
1.技術現狀和面臨的難題與挑戰
計算電磁學領域中最常用的數值計算方法主要有三種,分別為:時域有限差分(finite-difference time-domain, FDTD)法,有限元法(finite element method, FEM)和矩量法(method of moment, MoM)。隨著人們在電磁學領域研究的不斷深入,電磁工程問題主要呈現出寬頻帶化、復雜化的特點。這就對數值方法提出了兩個方面的要求:一方面,直接在時域對寬頻帶特性的時變電磁現象進行分析和計算;另一方面,實施簡單,具有普遍性。正是由于同時具有這兩方面的優點,針對要解決的具體問題,本項目研究的高頻不規則的輻射特點,FDTD法可更適用于該類復雜電磁問題的求解。
盡管電磁場的感應場-輻射場計算方法已開展了大量的研究,然而,高頻輻射且不規則電磁場的場分布計算在現階段仍面臨著難題與挑戰,主要體現在以下幾個方面。
第一方面,目前,一般延伸線的場分布計算大多數是遠場計算。高頻輻射且不規則電磁場感應場-輻射場場分布這一特定場景,其時域近場計算及特征分析鮮有報道。
第二方面,求解電磁場分布問題的數值方法大部分都是傳統FDTD、MoM、FEM等方法。而對于非對稱結構,其網格劃分存在軸線上網格遠多于其他方向的網格的問題,不易求解。而且常規方法需求內存消耗以保證其計算精度與計算效率。所以有必要對此類改進方法深入研究如何保證較低內存消耗的同時,也保證其有效的計算精度與效率。并進一步擴展數值方法在電磁學領域的應用。
第三方面,大型雷達周邊瞬時脈沖頻譜范圍大,基于譜域分解的有限元方法難以適用。而時域有限元方法同樣計算復雜且受時間穩定性條件限制。
2.基于改進FDTD和等效計算區域分解計算方法
為解決大型雷達周邊瞬時脈沖電磁場分布計算問題,提出一種基于改進FDTD和等效計算區域分解的反演計算技術,實現空間時域電場分布計算、近-遠場變換電磁計算以及電磁圖形顯示。該計算方法的流程具體如下圖所示:
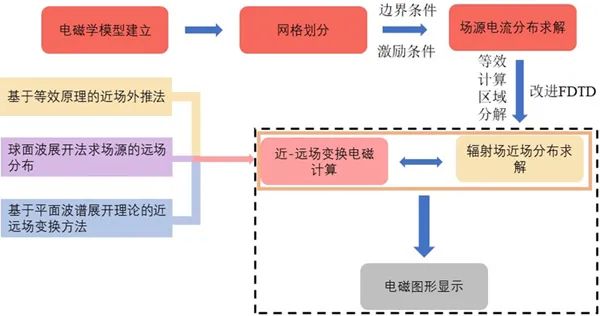
圖2-1、基于改進FDTD和等效計算區域分解的反演計算技術流程圖
2.1. 基于節點變量區域分解的WLP-FDTD法
傳統無條件穩定WLP-FDTD法通過將WLP作為時域基函數,將麥克斯韋旋度方程中的電場和磁場分量分別展開,再使用伽略金法加權求內積,消除時間項后用中心差分格式離散所有場分量的空間導數。通過以上步驟,得到以下兩個電場分量的隱式求解方程:
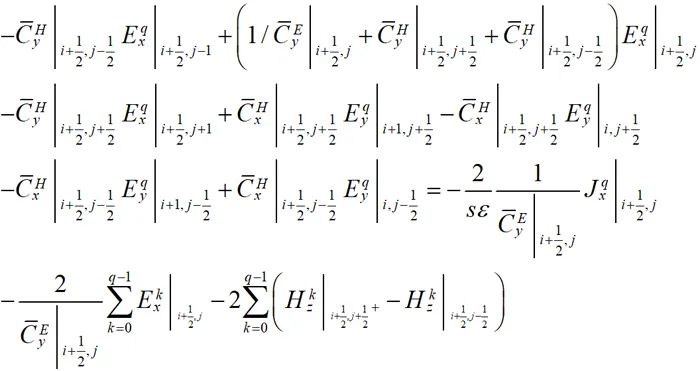
(2-1)
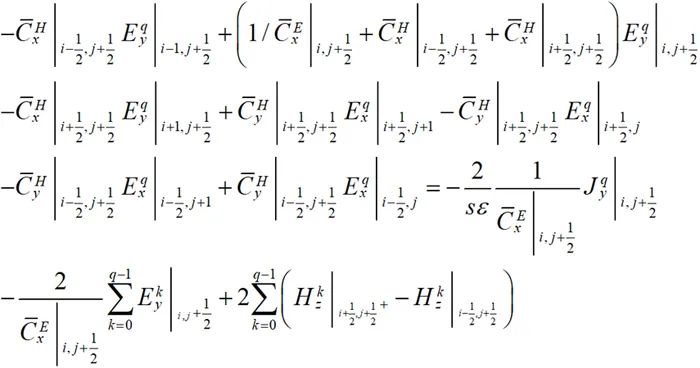
(2-2)
其中每個電場與其周圍的6個電場相互耦合,構成一個線性方程組進行聯立求解。場分量的分布如圖2-2所示。該線性方程組的每一行只含有7個非零元素,是一個稀疏陣。通過將(2-1)和(2-2)寫成如下的矩陣形式:
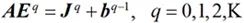 ?(2-3)
?(2-3)
其中,A為系數矩陣,Eq為待求的場分量,Jq為已知的激勵源,bq-1為所有低階已知場分量的和。計算得到的電場Eq只是每個場分量在計算空間中任意一點以WLP為基函數展開式中的系數。要得到計算區域中任意一點的時域場信息,需將這些系數代入展開式中即可求得具體場值。
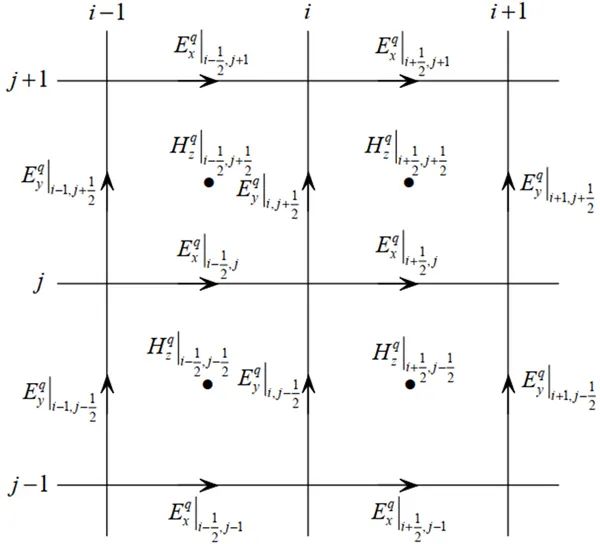
圖2-2、TEz波情況下WLP-FDTD電場和磁場分量在空間的分布
無條件穩定WLP-FDTD方法盡管在計算效率上相比其他FDTD已有較大提升,但其產生的大型稀疏矩陣仍有進一步優化的空間。對此,基于節點變量的子區域劃分思想,我們提出了一種更普遍和高效的區域分解技術,將隱式無條件穩定WLP-FDTD產生的大型稀疏矩陣劃分成若干個互不耦合的小矩陣,通過獨立求解每個小矩陣來提高數值仿真的效率。這種區域分解技術的優勢在于,全局Schur Complement矩陣可由所有子區域的局部Schur Complement矩陣和子區域之間的耦合矩陣直接組成,因此計算效率可被進一步提升。其中區域分解思想由圖2-3所示。
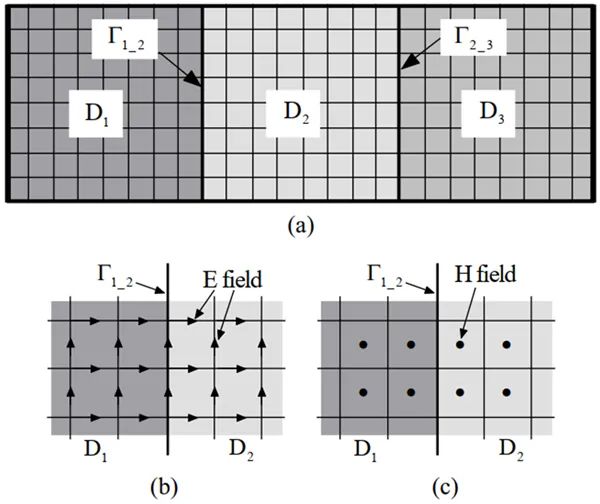
圖2-3 區域分解技術示意圖。(a)二維計算區域劃分為三個子區域;(b)基于棱邊變量的子區域劃分方式;(c)基于節點變量的子區域劃分方式
在基于節點變量的區域分解技術中,首先以均勻的正方形網格離散整個計算區域,再將計算區域劃分成3個子區域,如圖2-3(a)所示。對于特殊的仿真結構,可以使用非共形區域分解技術在不同子區域內部獨立剖分網格,此時子區域之間的分界面需要更復雜的處理。劃分子區域后,對矩陣系統的元素重新排序,依次排列所有完全屬于子區域內部的矩陣元素,再將所有位于分界面上的矩陣元素放在最后面,即可得到基于節點變量劃分子區域的Schur Complement系統。對于其中的任意一個子區域,局部Schur Complement系統會生成一個只包含位于分界面的場分量的方程組。因此,整個計算區域的全局Schur Complement系統可由局部Schur Complement系統與各個子區域之間的耦合子矩陣直接組成。由此可節省計算資源,提高計算效率。
2.2. 等效區域的場分布計算
傳統計算電磁學方法常需利用計算區域內所有網格點計算觀測面位置的場分布。盡管全局計算區域(Global Calculation Area, GCA)保證了良好的計算精度,但影響了內存消耗和計算效率。因此,研究了一種等效計算區域(Equivalent Calculation Area, ECA)優化劃分與輻射場場分布計算方法,以此提升算法綜合性能。
2.2.1. GCA場分布計算
時域輻射場觀測面計算區域模型中時域輻射場分布觀測區域為高頻中心軸線周圍一定半徑的柱狀區域,該半徑分別為0.3m、0.5m、1m和10m。時域輻射場觀測面可假設為整個柱狀區域沿高頻部分的剖分。因此,根據近場分布計算相關內容,觀測面上的時域輻射場場分布計算為:
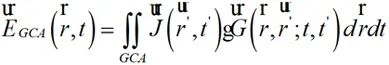
(2-4)
其中,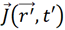 為第t'時刻高頻線上的
為第t'時刻高頻線上的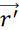 位置矢量處的電流密度,
位置矢量處的電流密度,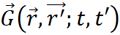 為
為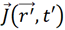 第t時刻映射至時域輻射場觀測面的
第t時刻映射至時域輻射場觀測面的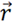 位置矢量處的格林函數,
位置矢量處的格林函數,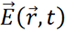 為第t時刻時域輻射場觀測面
為第t時刻時域輻射場觀測面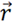 位置矢量處的該點處的電場強度。GCA為整個電纜結構的全局計算區域。
位置矢量處的該點處的電場強度。GCA為整個電纜結構的全局計算區域。
然而,一方面,半徑為1m和10m的柱狀觀察區域極大,大量網格的剖分十分不利于內存消耗和計算效率。這對仿真驗證研究工作的開展將有極為嚴峻的挑戰。另一方面,設一個區域長/寬/厚尺寸約為800mm×10mm×0.5mm,其長寬比和長厚比高至80和1600,使得沿軸線上的網格剖分增多。因此,GCA場分布計算法難以適用于高頻分布的輻射場場分布計算。
2.2.2 ECA優化劃分與場分布計算
ECA網格綜合優化劃分影響著輻射場場分布計算精度。最優ECA劃分可按照下列方法求取。
一方面,根據式(2-4),基于ECA網格劃分的時域輻射場觀測面上的場分布計算為:
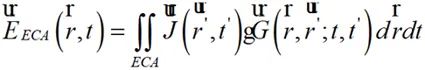
(2-5)
如圖2-5所示。以ECA網格長為參量掃描,將計算網格劃分為ECA1,ECA2,?,ECAN。各場分布差量計算為:
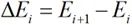 ?(2-6)
?(2-6)
其中:
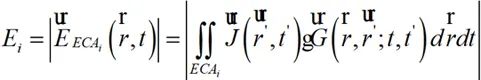
(2-7)
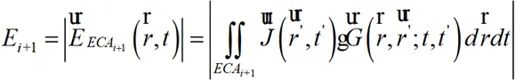
(2-8)
式中i=1,2,?,N-1。當ΔEi無限逼近于0,此時ECAi和ECAi+1網格劃分可認為是最優ECAopt。此時,時域輻射場觀測面上的場分布計算為:
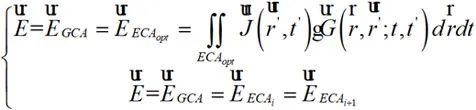
(2-9)
另一方面,可考察ECA場分布計算與GCA場分布計算差量:
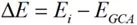 ?(2-10)
?(2-10)
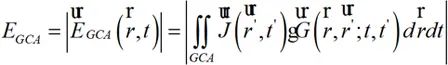
(2-11)
式中i=1,2,?,N,當ΔE無限逼近于0,此時可認為ECAi網格劃分是最優的ECAopt。
ECA場分布計算可將全局計算區域等效為有效計算區域,ECA最優劃分可對不同柱狀觀測區域的場分布再次計算提供最優計算區域,以此提高計算效率,減小計算內存損耗。
2.3 近-遠場變換電磁計算
2.3.1基于等效原理的近場外推法
為了根據以上方法在近場有限區域計算所得的電磁場,可利用等效原理與惠更斯原理進行近場外推計算,從而獲得遠區的輻射場。基于等效原理的近場外推法是先在場源周圍引入外推數據儲存邊界面A,如圖2-4所示。假設A面外為自由空間。如果保持界面A處場EH的且向分量不變,而令A面內的場為零,根據唯一性定理,這種情況與原始情況在分界面A以外的場分布不變,A面處的電場與磁場用EA、HA表示。
根據邊界條件與等效原理,A面處的等效面電流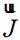 和等效面磁流
和等效面磁流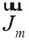 ,由以下公式計算獲得:
,由以下公式計算獲得:
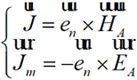 ?(2-12)
?(2-12)
式中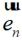 為分界面A的外法向。原問題變為A面處面電流
為分界面A的外法向。原問題變為A面處面電流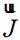 和面磁流
和面磁流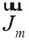 在全空間為自由空間時的輻射問題。
在全空間為自由空間時的輻射問題。
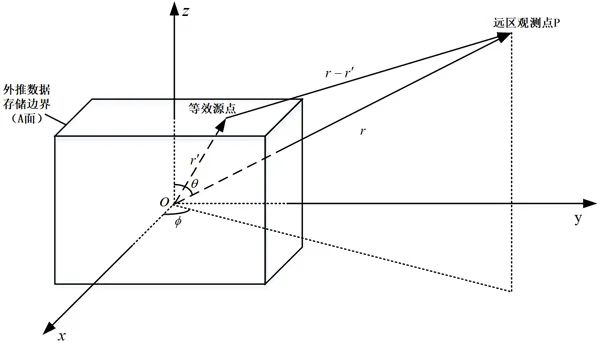
圖2-4、由數據存儲邊界外推遠區場示意圖
對于時諧場情況,均勻介質匯總存在電流與磁流時的麥克斯韋方程為:
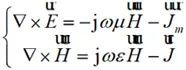 ?(2-13)
?(2-13)
電流與磁流的輻射場為:
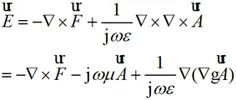
(2-14)
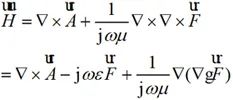
(2-15)
其中
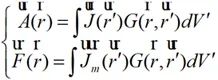
(2-16)
式(2-16)中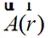 和
和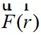 為矢量勢函數;
為矢量勢函數;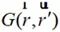 為自由空間格林函數,其中三維情況中自由空間的格林函數為:
為自由空間格林函數,其中三維情況中自由空間的格林函數為:
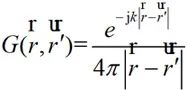 ?(2-17)
?(2-17)
其中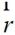 ,
,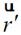 分別為觀察點和等效源點位置矢量,如圖1所示。可以取遠區近似:
分別為觀察點和等效源點位置矢量,如圖1所示。可以取遠區近似:
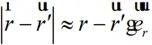 ?(2-18)
?(2-18)
因此,自由空間三維遠區格林函數可近似為:
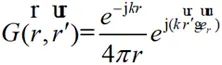
(2-19)
將公式(2-19)代入到公式(2-16)可得:
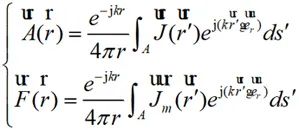
(2-20)
對遠區場可以分離出球面波因子。電流矩和磁流矩分別為:
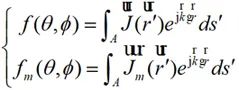
(2-21)
公式(2-21)中,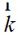 為散射波矢量:
為散射波矢量:
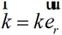 ?(2-22)
?(2-22)
在遠區,公式(2-14)、(2-15)可中的▽算子可以用 取代,所以:
取代,所以:
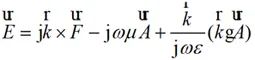
(2-23)
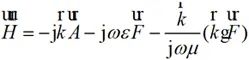
(2-24)
將公式(2-23)右端轉換為球坐標分量形式:
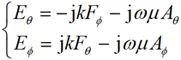 ?(2-25)
?(2-25)
同理,由(2-24)式得到的遠區場球坐標分量為:
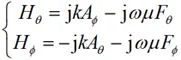 ?(2-26)
?(2-26)
將(2-25)式用電流矩和磁流矩表示為:
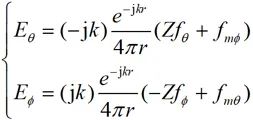
(2-27)
其中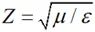 為波阻抗。遠區
為波阻抗。遠區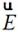 和
和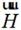 的關系如同平面波。
的關系如同平面波。
若已知的分界面A上電場分布計算是在直角坐標系進行的,也即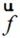 、
、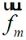 是直角坐標分量。可以將公式(2-25)轉換為:
是直角坐標分量。可以將公式(2-25)轉換為:
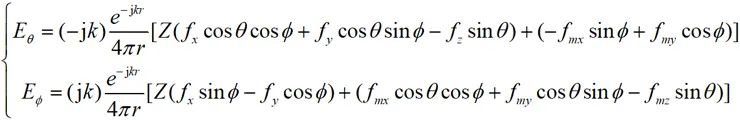
(2-28)
根據(2-27)或(2-28)式即可求解出目標遠場分布。
2.3.2 球面波展開法求場源的遠場分布
運用電磁場的球面展開理論,在已知源的電流分布情況下,將自由空間中場源產生的電磁場分解為球坐標系中的標量波函數的線性組合。通過計算該求和公式中標量波函數分別對應的各項系數,從而求解出場源的遠區場。
設r≥R的球面內包括了整個場源,當在r≥R的區域時的各個觀測點處于無源區,電磁場是無散無旋的,在該區域的電場可以展開為球面波函數的線性疊加,表示為:
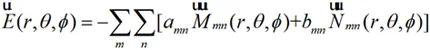
(2-29)
式中,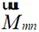 、
、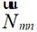 均為矢量波函數,表達式如下所示
均為矢量波函數,表達式如下所示
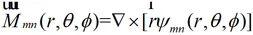 ?(2-30)
?(2-30)
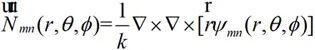
(2-31)
上式的Ψmn是標量波函數,為齊次標量Helmholtz方程在球坐標系下的解,在無限大的自由空間中,Ψmn的表達式為:
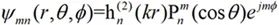 ?(2-32)
?(2-32)
其中,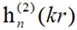 為第二類n階Hankel函數,
為第二類n階Hankel函數,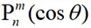 為第一類連帶Legendre函數。
為第一類連帶Legendre函數。
通過求解場強的r分量可以獲得各項系數amn、bmn,如下式所示:
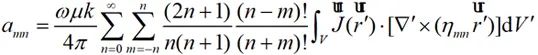
(2-33)
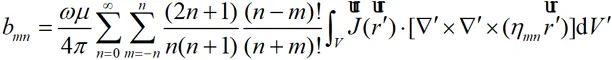
(2-34)
其中,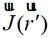 為場源的電流分布,
為場源的電流分布,
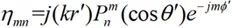 ?(2-35)
?(2-35)
由公式(2-33)、(2-34)可知,系數amn和bmn均與距離r無關,因此該系數適合任何場點。將(2-33)、(2-34)代入(2-35)式即可求得無源區域的場分布。
當觀測點處于場源的遠場區時,由于kr→∞,則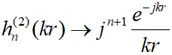 ,
,
因此:
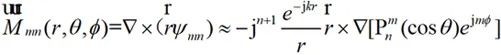
(2-36)
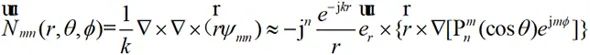
(2-37)
將以上結果代入到(2-29)中可得:
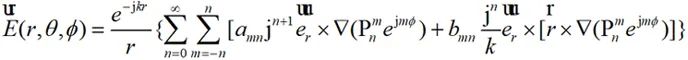
(2-38)
因此,在已知場源的電流分布的情況下,可以計算獲取在場源的遠場區域內觀測點的電場分布。該方法中球面波展開式的級數求和比積分求積簡單,適合數值計算。
2.3.3 基于平面波譜展開理論的近遠場變換方法
假設自由空間中,無源區域內某觀測點的電場為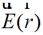 ,可以通過傅里葉變換在空間頻域展開:
,可以通過傅里葉變換在空間頻域展開:
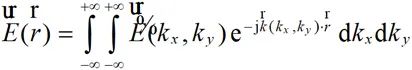
(2-39)
其中,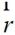 為觀測點的位置矢量,kx和ky分別表示自由空間中波矢量
為觀測點的位置矢量,kx和ky分別表示自由空間中波矢量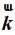 的x和y分量,且
的x和y分量,且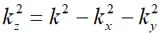 。
。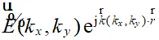 為沿?
為沿?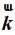 方向的平面波。
方向的平面波。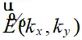 為傅里葉變換后每個方向的平面波對應的頻譜。上式說明,空間任意一點的電場可以表示成沿各個不同方向的平面波的積分求和。如果想要獲取空間中的場,我們只需要求得觀測點沿不同方向傳播的頻譜,即可獲得該觀測點的電場。
為傅里葉變換后每個方向的平面波對應的頻譜。上式說明,空間任意一點的電場可以表示成沿各個不同方向的平面波的積分求和。如果想要獲取空間中的場,我們只需要求得觀測點沿不同方向傳播的頻譜,即可獲得該觀測點的電場。
由于無源區域內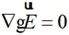 ,可以獲得:
,可以獲得:
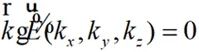 ?(2-40)
?(2-40)
所以:
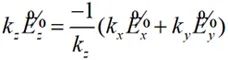
(2-41)
假設已知在場源的近場區域內z=d1平面上的切向電場,該平面上切向電場可根據公式(2-39)表示為:
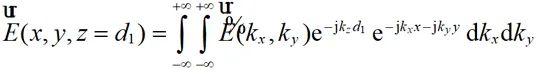
(2-42)
因此將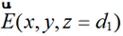 進行傅里葉變換即可獲得不同方向平面波對應的頻譜
進行傅里葉變換即可獲得不同方向平面波對應的頻譜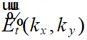 :
:
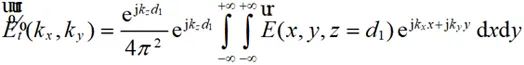
(2-43)
將(2-43)代入(2-41)可求出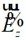 ,因此:
,因此:
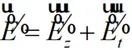 ?(2-44)
?(2-44)
將公式(2-44)中計算獲得的頻譜代入到(2-39)中,即可獲得在場源外自由空間中的電場分布。當觀測點距離場源的距離r很遠時,可以通過駐相法對運算進行簡化。進一步的,由于當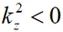 ,也即
,也即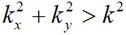 時,平面波沿z軸呈指數衰減,高波數時對應的衰減更大,在計算遠場時可以忽略。
時,平面波沿z軸呈指數衰減,高波數時對應的衰減更大,在計算遠場時可以忽略。
3.項目內容結果
結合電磁場中區域分解技術,將高頻輻射裝置分解提取出相應的幾何參數,進行了負載短路周邊輻射場的電磁仿真工作。
3.1. 短路負載
短路負載模型結合轉接裝置的內部結構和材料屬性,進行如下的仿真設置:轉接裝置的底座部分設置為εr=2.1,tanδe=0.001的電介質材料,然后兩根金屬引線與短路線相連,引線的末端設置為集總端口激勵。
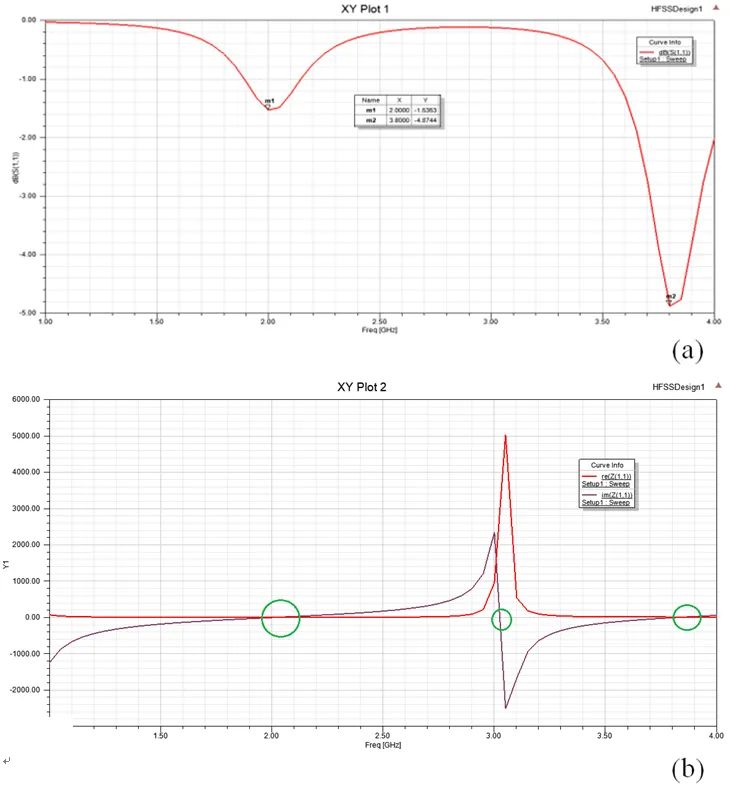
圖3-1 短路負載電磁仿真(a)短路負載S11參數;(b)短路負載輸入阻抗
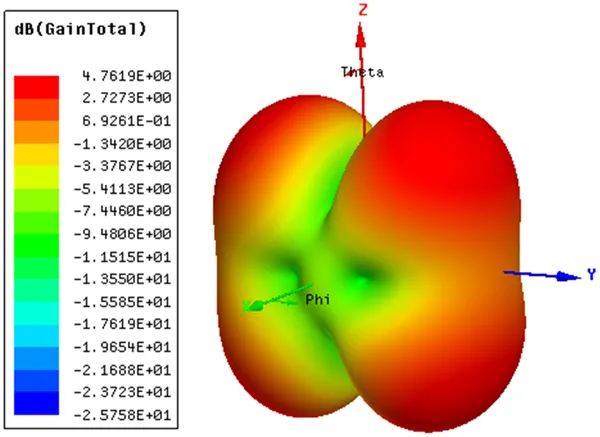
圖3-2 在3.8GHz頻點處的增益方向圖
短路負載S11參數和輸入阻抗分別如圖3-1(a)和(b)所示。其中,仿真計算的頻段為1~4GHz。從輸入阻抗曲線上看,在1~4GHz頻段內,一共出現3處輸入電抗為0的頻點,代表三個諧振點,其中3.8GHz處的輸入阻抗與50Ω最接近。因此,可研究該頻點的增益方向圖,如圖3-2所示。不考慮匹配效率,最大增益為4.7619dBi,倘若考慮匹配效率,最大實際增益為3.0517dBi。
3.2. 整體聯合仿真
短路負載與整體結構的仿真,完成近場分布計算。該模型在Y方向上的最大長度約為6.4cm,在X方向上的最大長度為2.78cm。設中心為坐標原點O,以邊長為40cm的正方體為近場觀測面。若該觀察面邊長足夠大,遠大于該長度即40cm、且計算區域同樣很大,如要求的1m/10m的柱狀區域,那么計算如此大的區域則會占用極大的計算資源(邊長60cm的正方體空氣盒子占用內存超過1TB)。
表3-1遠場條件和輻射增益
| 頻率(GHz) | 遠場距離(m) | 增益(dBi) | 實際增益(dBi) |
| 0.4 | 1.2 | -8.22 | -35.81 |
| 1 | 0.48 | -1.1 | -26.05 |
| 2.1 | 0.32 | 5.05 | -0.77 |
| 4.1 | 0.32 | 5.32 | 4.05 |
| 6 | 0.32 | 5.46 | 3.85 |
如果以D=6.4cm作為短路負載的最大尺寸,根據天線教材上面給出遠場距離條件:
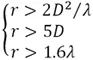 ?(4-1)
?(4-1)
仿真頻段為0.4~6GHz,下表即為不同頻點的遠場距離和增益:
該頻段的S11參數曲線如圖3-3(a)所示,盡管分別在2.1GHz、4.1GHz和6GHz附近存在諧振點,但輸入阻抗與50Ω相差較大。將頻段拓展至6.5GHz時,其輸入阻抗為42.836+j5.6473Ω,S11參數小于-20dB。短路負載從2GHz開始能夠進行有效的電磁輻射,增益在5dBi以上;在1GHz以下,增益非常低。整體結構的場強方向圖如圖3-3(b)所示,選取的頻點為0.4GHz。其方向性系數是1.55dBi,即1.43,呈現為全向輻射狀態,最大輻射方向出現在線圈所在平面,可等效為電小環輻射。圖3-4至圖3-7分別為0.4GHz、2.1GHz、4.1GHz和6GHz處的電場和磁場分布。而圖3-8為不同頻點下的增益方向圖。從方向圖的形狀來看,金屬線圈的周長接近于一個波長,短路負載的輻射方向圖和一波長的大環天線方向圖形狀非常接近。
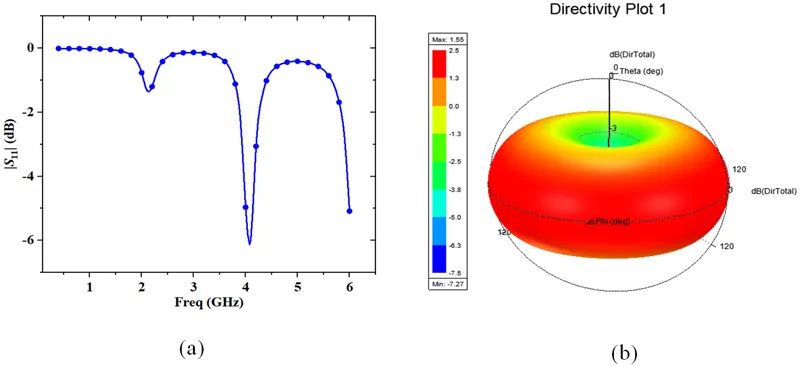
圖3-3 (a)S11參數曲線;(b)0.4GHz處的場強方向圖;
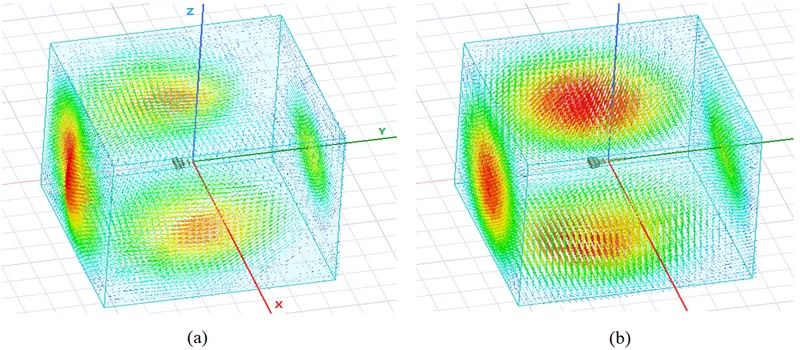
圖3-4 0.4GHz處場分布。(a)電場;(b)磁場;
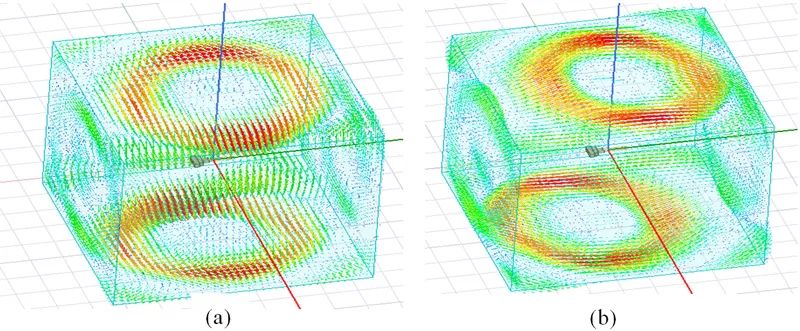
圖3-5 2.1GHz處場分布。(a)電場;(b)磁場;
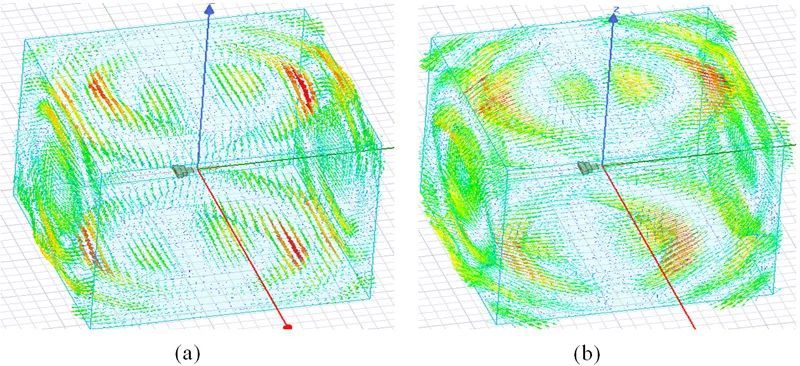
圖3-6 4.1GHz處場分布。(a)電場;(b)磁場;
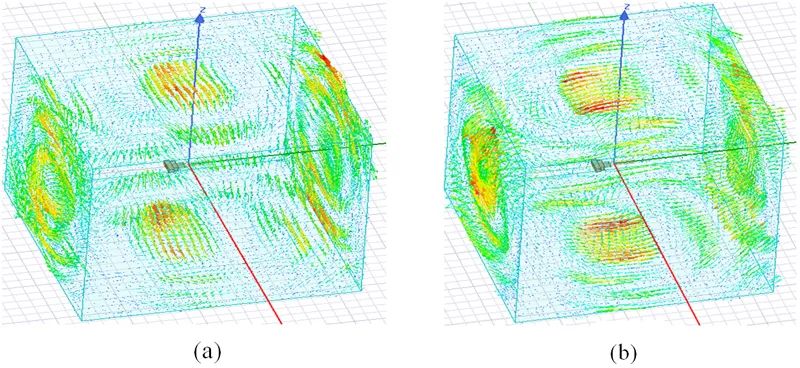
圖3-7 6GHz處場分布。(a)電場;(b)磁場;
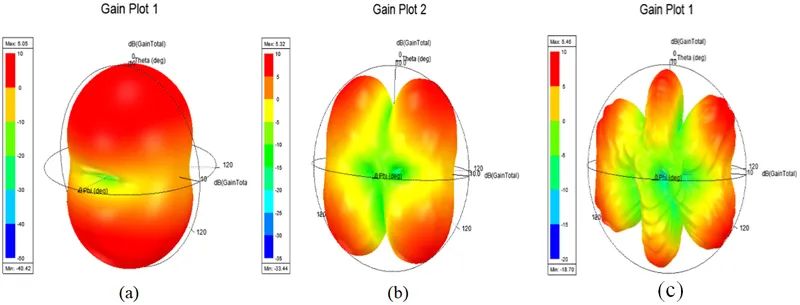
圖3-8 增益方向圖。(a)2.1 GHz;(b) 4.1 GHz;(c) 6 GHz
4.技術及應用
基于此改進FDTD和等效計算區域分解的計算電磁技術能夠有效反演還原大型復雜雷達系統的周邊電磁場場強,分析出系統工作時對周圍環境的影響,從而做出精確的反干擾或者其他規避措施,也可以用于分析被探測目標物體的電磁散射,計算出電磁場場強,建立分布模型的賦形場,從而還原出物體的電磁特性,進而進行物體的成像還原或者跟蹤等上層應用。
原文標題:大型相控陣雷達周邊復雜區域的電磁反演技術
文章出處:【微信公眾號:微波射頻網】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
電磁
+關注
關注
15文章
1075瀏覽量
51721 -
雷達
+關注
關注
50文章
2903瀏覽量
117343
原文標題:大型相控陣雷達周邊復雜區域的電磁反演技術
文章出處:【微信號:mwrfnet,微信公眾號:微波射頻網】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
KiCon演講回顧(五):電磁仿真新流程:KiCad XAO 到 Elmer FEM

電磁干擾與電磁輻射的區別 EMI電磁干擾與電力系統的關系
EMI電磁干擾測試方法 如何有效防止EMI電磁干擾
如何使用近場探頭測量輻射?

淺談邊緣計算在綜合管廊監控系統應用
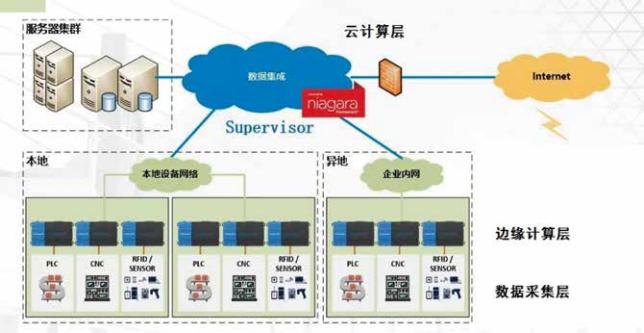




 基于改進FDTD和等效計算區域分解的輻射場反演綜合計算電磁方法
基于改進FDTD和等效計算區域分解的輻射場反演綜合計算電磁方法
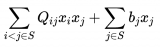













評論