CRC是CyclicRedundancyCheck的縮寫,是一種通過額外冗余bit來檢查數據完整性的一種方法。一個比較容易類比的方法就是除法操作。例如我們有數據512,我們將512除以11得到46余數是6。那么我們可以將6作為校驗信息一起傳遞給對方。接收端收到512和校驗信息6后,也做相同的除法操作,如果得到的余數與收到的校驗信息一致,我們認為收到的數據大概率是完整的。 我們將十進制轉換成二進制,重新看一遍過程,原始數據是
512 = 10 0000 0000 11 = 1011 10 0000 0000/1011 = 100 0110 余 110
當傳輸過程中某一個bit被反轉了,例如: 10 0001 0000 (528)
接收端使用收到的數據進行除法操作,將會得到:
10 0001 0000/1011 = 100 1000 余 0
那么這個校驗信息就不一樣了,所以接收端認為數據或者校驗信息在傳輸過程中可能出現了錯誤。
為了使得校驗比較方便,我們可以將需要校驗的信息放在數據的后面。由于除數是11(1011b),余數有可能是0(0000b)到10(1010b),所以我們可以將原數據向左移4位,空出來的空間存放校驗信息。左移4位相當于把原數據乘以了24,即十進制的16。 512*16 = 8192 二進制表示:10 0000 0000 0000b 然后用8192/11 = 744 余8 不難算出,只要將8192加上3,這個新的數就可以被11整除。 所以我們可以將3作為這個原數據的校驗信息,并放在原數據的后面一起傳送,即: 10 0000 0000 0011b
如果接收端接收到的數據無法被11整除,即有余數,那么證明接收到的內容可能在傳輸過程中被修改了。 例如,仍然是原數據的第六個bit被反轉了,即: 10 00010000 0011b (8451)
那么接收端對接收到的內容進行運算會發現: 8451/11 = 768 余 3
并不能被11整除,所以內容可能在傳輸過程中被修改了。 我們仔細觀察會發現,原本的信息是可以被11整除的,多出來的部分是由于某個bit反轉而引起的,我們單獨將該信息拿出來,可以得到: 1 0000 0000b (256) 如果將這個錯誤信息除11,我們會發現: 256/11 = 23 余 3 也是余3,是不是發現了什么?沒有錯,導致最后整個信息不整除的主要原因,是因為反轉的bit與其所在的位置所表達的數不能夠被11整除。 因為我們在數字世界傳送信息的時候大部分都是01表示的二進制代碼,所以信息中有任意一個bit被反轉,都是2的多少次冪。所以只要除數不是偶數且不是1就可以檢測出任意一個bit的錯誤。例如3(11b),5(101b),7(111b)等等。
由于除法操作可能需要借位,在實際的CRC計算中,采用的是異或(XOR)操作而避免了借位。同樣的,如果數據仍然是10 0000 0000b,而‘除數’是1011b,這個‘除數’也被稱之為二項式(polynomial),也可以表達成 X3+X+1。 那么我們一樣將原數據左移,只不過這次我們只移動3位且補0,因為不使用減法操作,只要異或完的結果少于4位,我們就把那3位數作為‘余數’。具體操作如下: 首先將10 0000 0000b左移3位: 1 0000 0000 0000b,然后用1011b作為‘除數’: 異或操作的真值表: 0 xor 0 = 0 0 xor 1 = 1 1 xor 0 = 1 1 xor 1 = 0 其實就是相同就是0,不一樣就是1。下面是長除的整個過程:
1011100101 1011/1000000000000 1011 1100 1011 1110 1011 1010 1011 1000 1011 1100 1011 111 ----------‘余數’
這里可以看到我們得到的‘余數’與實際的除法得到的余數有所不同,那么使用這種方式有什么好處呢? 我們接著往下看。
這個‘余數’被稱為CRC3的值,作為校驗信息可以直接替換掉數據的最后3位,這3位是原數據左移后,補了0的3個位置。當計算出CRC3的值后,可以直接把111b添加在后面,即: 1 0000 0000 0111b 因為異或的原因,這個數正好可以被1011b通過長除的方法整除,便利性與傳統除法來說要好不少,大家可以參考前面標紅的那句話。另外就是異或操作在數字設計中也比較容易實現。 接下來我們繼續分析一下檢錯能力,前面提到設計過的二項式可以保證任意一個bit反轉都可以被檢測出來。如果需要保證連續相鄰的兩個bit都反轉了也可以被檢測出來怎樣設計呢?那我們可以分析一下連續兩個bit都反轉的情況,錯誤信息的規律。例如我們可以用Xn+Xn-1來表示連續兩個bit都反轉的情況。因為原來的兩個bit與11b進行異或都會取反,所以我們可以用Xn+Xn-1來表示11b并處在任意的位置。通過提取公因數得到: Xn+Xn-1 = Xn-1(X+1) 所以我們設計的二項式只要不能被X+1整除,那么連續兩個bit的錯誤信息就無法被該二項式整除。因此類似X2+1 或者X3+1這種二項式就是不錯的選擇。 Note: 二項式 X2+1就是101b 二項式 X3+1就是1001b
原文標題:PCIe核心技術之CRC系列1 - CRC3
文章出處:【微信公眾號:ssdfans】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
crc
+關注
關注
0文章
199瀏覽量
29438 -
PCIe
+關注
關注
15文章
1224瀏覽量
82446
原文標題:PCIe核心技術之CRC系列1 - CRC3
文章出處:【微信號:SSDFans,微信公眾號:SSDFans】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
pcie擴展槽的使用技巧
如何測試PCIe插槽的速度
三星電子成功收購英國初創公司,致力開發AI核心技術
【大語言模型:原理與工程實踐】核心技術綜述
Linux內核PCIE基礎知識整理
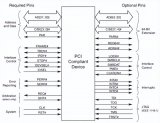




 PCIe核心技術CRC基礎知識
PCIe核心技術CRC基礎知識

















評論