谷歌 AI 最近一項研究表明，利用機器學(xué)習(xí)和硬件加速器能夠改進流體模擬，且不損害準(zhǔn)確率或泛化性能。

流體數(shù)值模擬對于建模多種物理現(xiàn)象而言非常重要，如天氣、氣候、空氣動力學(xué)和等離子體物理學(xué)。流體可以用納維 - 斯托克斯方程來描述，但大規(guī)模求解這類方程仍屬難題，受限于解決最小時空特征的計算成本。這就帶來了準(zhǔn)確率和易處理性之間的權(quán)衡。

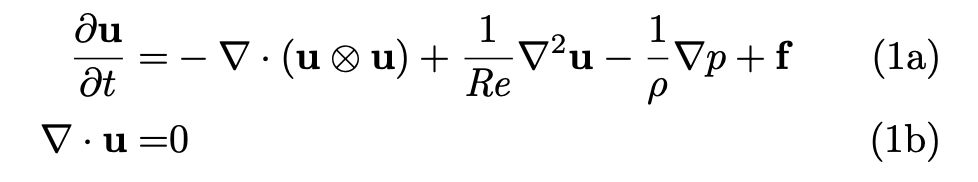
不可壓縮流體通常由如上納維 - 斯托克斯方程來建模。 最近，來自谷歌 AI 的研究人員利用端到端深度學(xué)習(xí)改進計算流體動力學(xué)（CFD）中的近似，以建模二維渦流。對于湍流的直接數(shù)值模擬（direct numerical simulation, DNS）和大渦模擬（large eddy simulation, LES），該方法獲得的準(zhǔn)確率與基線求解器相同，而后者在每個空間維度的分辨率是前者的 8-10 倍，因而該方法實現(xiàn)了 40-80 倍的計算加速。在較長模擬中，該方法仍能保持穩(wěn)定，并泛化至訓(xùn)練所用流以外的力函數(shù)（forcing function）和雷諾數(shù)，這與黑箱機器學(xué)習(xí)方法正相反。此外，該方法還具備通用性，可用于任意非線性偏微分方程。

論文地址：https://arxiv.org/pdf/2102.01010.pdf 該研究作者之一、谷歌研究員 Stephan Hoyer 表示：這項研究表明，機器學(xué)習(xí) + TPU 可以使流體模擬加速多達兩個數(shù)量級，且不損害準(zhǔn)確率或泛化性能。

至于效果如何呢？論文共同一作 Dmitrii Kochkov 展示了該研究提出的神經(jīng)網(wǎng)絡(luò)與 Ground truth、基線的效果對比： 首先是雷諾數(shù) Re=1000 時，在 Kolmogorov 流上的效果對比：

其次是關(guān)于衰變湍流（decaying turbulence）的效果對比：

最后是雷諾數(shù) Re=4000 時，在更復(fù)雜流上的效果對比：

方法簡介 用非線性偏微分方程描述的復(fù)雜物理系統(tǒng)模擬對于工程與物理科學(xué)而言非常重要。然而，大規(guī)模求解這類方程并非易事。 谷歌 AI 這項研究提出一種方法來計算非線性偏微分方程解的準(zhǔn)確時間演化，并且其使用的網(wǎng)格分辨率比傳統(tǒng)方法實現(xiàn)同等準(zhǔn)確率要粗糙一個數(shù)量級。這種新型數(shù)值求解器不會對未解決的自由度取平均，而是使用離散方程，對未解決的網(wǎng)格給出逐點精確解。研究人員將受分辨率損失影響最大的傳統(tǒng)求解器組件替換為其學(xué)得的組件，利用機器學(xué)習(xí)發(fā)現(xiàn)了一些算法。 如下圖 1a 所示，對于渦流的二維直接數(shù)值模擬，該研究提出的算法可以在每個維度的分辨率粗糙 10 倍的情況下維持準(zhǔn)確率不變，也就是說獲得了 80 倍的計算時間改進。該模型學(xué)習(xí)如何對解的局部特征進行插值，從而能夠準(zhǔn)確泛化至不同的流條件，如不同受力條件，甚至不同的雷諾數(shù)（圖 1b）。 研究者還將該方法應(yīng)用于渦流的高分辨率 LES 模擬中，獲得了類似的性能提升，在網(wǎng)格分辨率粗糙 8 倍的情況下在 Re = 100, 000 LES 模擬中維持逐點準(zhǔn)確率不變，實現(xiàn)約 40 倍的計算加速。

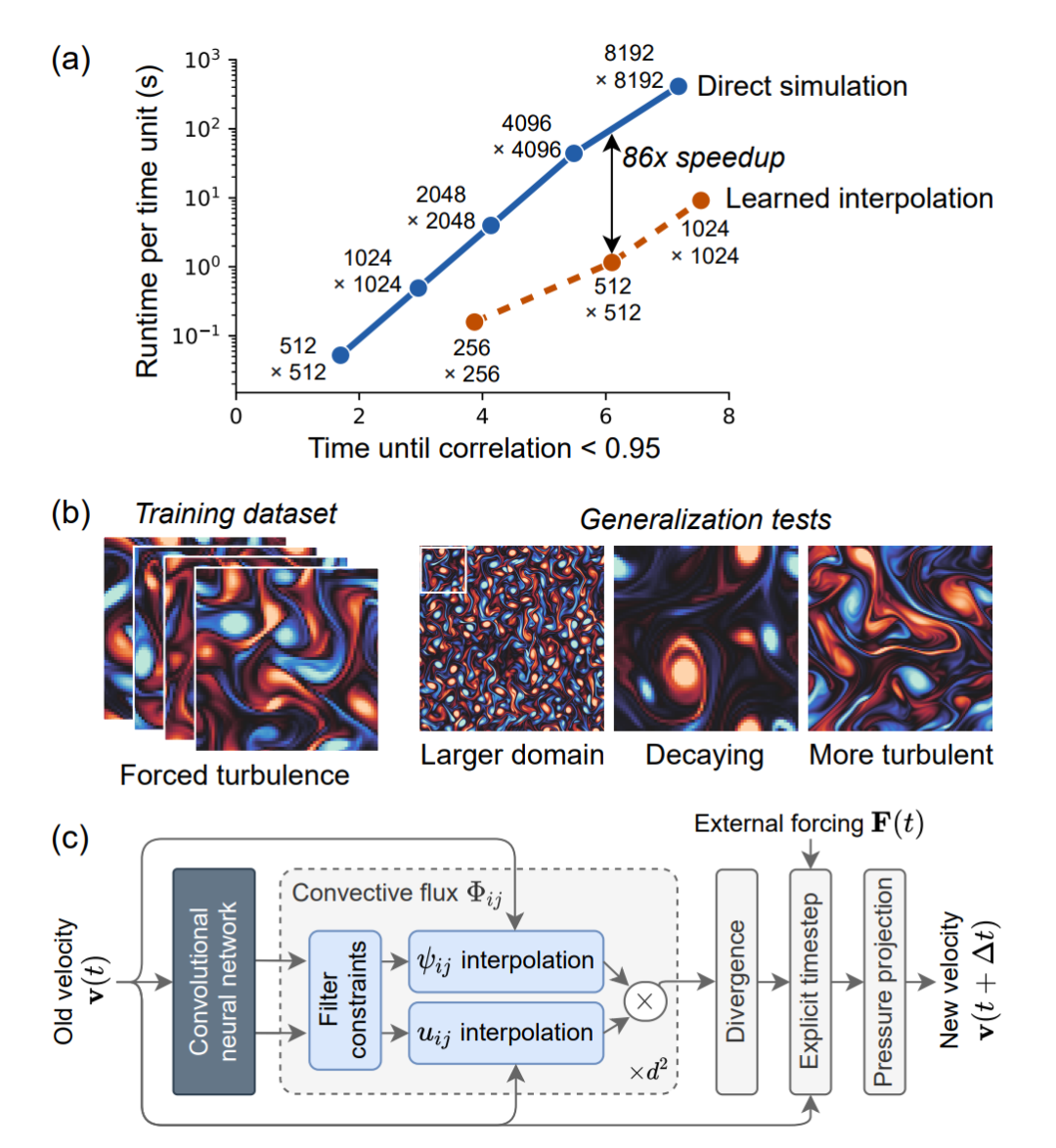
圖 1：該研究提出方法與結(jié)果概覽。a）基線（direct simulation）與 ML 加速（learned interpolation）求解器的準(zhǔn)確率與計算成本對比情況；b）訓(xùn)練與驗證樣本圖示，展示出該模型強大的泛化能力；c）該研究提出「learned interpolation」模型的單時間步結(jié)構(gòu)，用卷積神經(jīng)網(wǎng)絡(luò)控制標(biāo)準(zhǔn)數(shù)值求解器對流計算中學(xué)得的近似。 研究者使用數(shù)據(jù)驅(qū)動離散化將微分算子插值到粗糙網(wǎng)格，且保證高準(zhǔn)確率（圖 1c）。具體而言，將求解底層偏微分方程的標(biāo)準(zhǔn)數(shù)值方法內(nèi)的求解器作為可微分編程進行訓(xùn)練，在 JAX 框架中寫神經(jīng)網(wǎng)絡(luò)和數(shù)值方法（JAX 框架支持反向模式自動微分）。這允許對整個算法執(zhí)行端到端的梯度優(yōu)化，與密度泛函理論、分子動力學(xué)和流體方面的之前研究類似。

研究者推導(dǎo)出的這些方法是特定于方程的，需要使用高分辨率真值模擬訓(xùn)練粗糙分辨率的求解器。由于偏微分方程的動態(tài)是局部的，因此高分辨率模擬可以在小型域內(nèi)實施。 該算法的工作流程如下：在每一個時間步中，神經(jīng)網(wǎng)絡(luò)在每個網(wǎng)格位置基于速度場生成隱向量，然后求解器的子組件使用該向量處理局部解結(jié)構(gòu)。該神經(jīng)網(wǎng)絡(luò)為卷積網(wǎng)絡(luò)，具備平移不變性，因而允許解結(jié)構(gòu)在空間中是局部的。之后，使用標(biāo)準(zhǔn)數(shù)值方法的組件執(zhí)行納維 - 斯托克斯方程對應(yīng)的歸納偏置，如圖 1c 灰色框所示：對流通量（convective flux）模型改進離散對流算子的近似；散度算子（divergence operator）基于有限體積法執(zhí)行局部動量守恒；壓力投影（pressure projection）實現(xiàn)不可壓縮性，顯式時間步算子（explicit time step operator）使動態(tài)具備時間連續(xù)性，并允許額外時變力的插值。

「在更粗糙網(wǎng)格上的 DNS」將傳統(tǒng) DNS 和 LES 建模的界限模糊化，從而得到多種數(shù)據(jù)驅(qū)動方法。 該研究主要關(guān)注兩種 ML 組件：learned interpolation 和 learned correction。此處不再贅述，詳情參見原論文。 實驗結(jié)果加速 DNS 一旦網(wǎng)格分辨率無法捕捉到解的最小細(xì)節(jié)，則 DNS 的準(zhǔn)確率將快速下降。而該研究提出的 ML 方法極大地緩解了這一效應(yīng)。下圖 2 展示了雷諾數(shù) Re = 1000 的情況下在 Kolmogorov 流上訓(xùn)練和評估模型的結(jié)果。

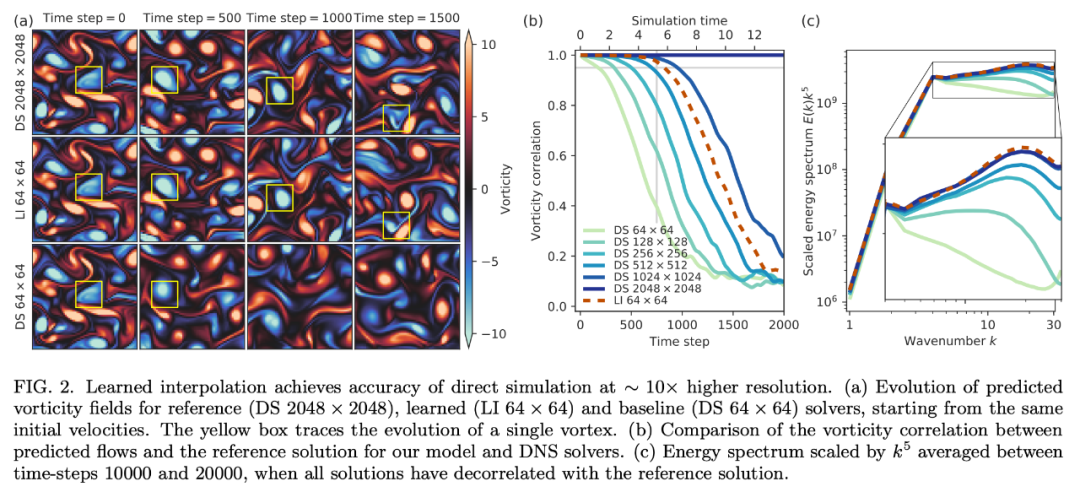
而就計算效率而言，10 倍網(wǎng)格粗糙度的情況下，learned interpolation 求解器取得與 DNS 同等準(zhǔn)確率的速度也要更快。研究者在單個谷歌云 TPU v4 內(nèi)核上對該求解器進行了基準(zhǔn)測試，谷歌云 TPU 是用于機器學(xué)習(xí)模型的硬件加速器，也適用于許多科學(xué)計算用例。在足夠大的網(wǎng)格大小（256 × 256 甚至更大）上，該研究提出的神經(jīng)網(wǎng)絡(luò)能夠很好地利用矩陣乘法單元，每秒浮點運算的吞吐量是基線 CFD 求解器的 12.5 倍。因此，盡管使用了 150 倍的算術(shù)運算，該 ML 求解器所用時間仍然僅有同等分辨率下傳統(tǒng)求解器的 1/12。三個維度（兩個空間維度和一個時間維度）中有效分辨率的 10 倍提升，帶來了 10^3/12 ≈ 80 倍的加速。 此外，研究者還考慮了三種不同的泛化測試：大型域規(guī)模；非受迫衰減渦流；較大雷諾數(shù)的 Kolmogorov 流。 首先，研究者將同樣的力泛化至較大的域規(guī)模。該 ML 模型得到了與在訓(xùn)練域中同樣的性能，因為它們僅依賴流的局部特征（參見下圖 5）。 然后，研究者將在 Kolmogorov 流上訓(xùn)練的模型應(yīng)用于衰減渦流。下圖 3 表明，在 Kolmogorov 流 Re = 1000 上學(xué)得的離散模型的準(zhǔn)確率可以匹配以 7 倍分辨率運行的 DNS。

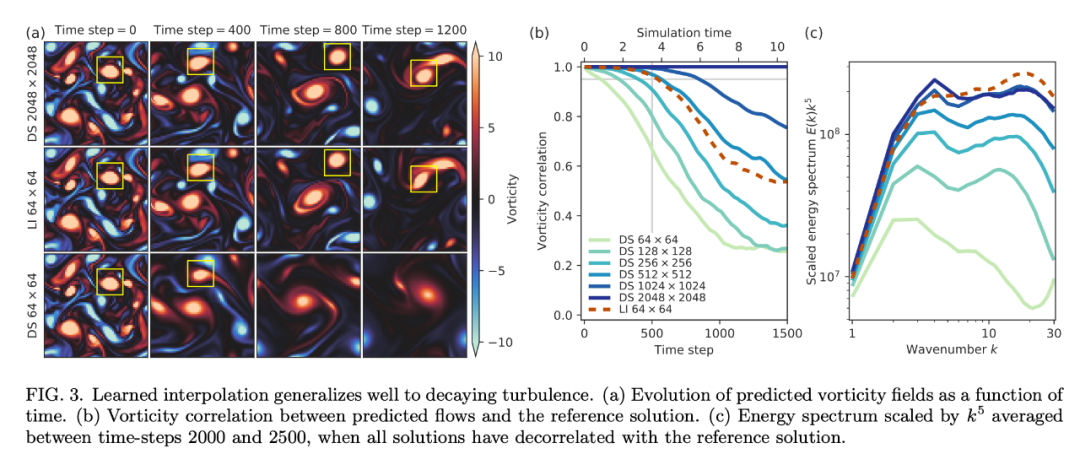
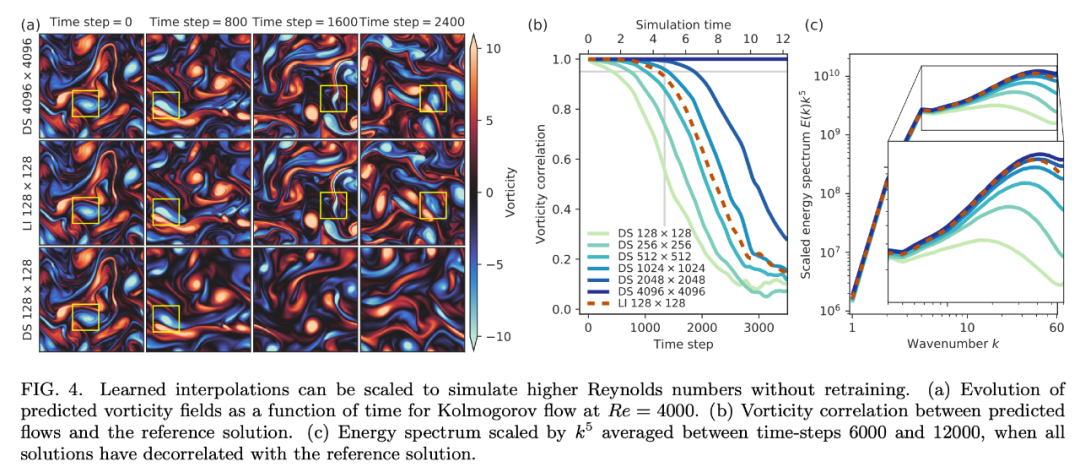
最后，該模型可以泛化至更高的雷諾數(shù)嗎？也就是更復(fù)雜的流。下圖 4a 表明，該模型的準(zhǔn)確率可以匹配以 7 倍分辨率運行的 DNS。鑒于該測試是在復(fù)雜度顯著增加的流上進行的，因此這種泛化效果很不錯。圖 4b 對速度進行了可視化，表明該模型可以處理更高的復(fù)雜度，圖 4c 的能譜進一步驗證了這一點。

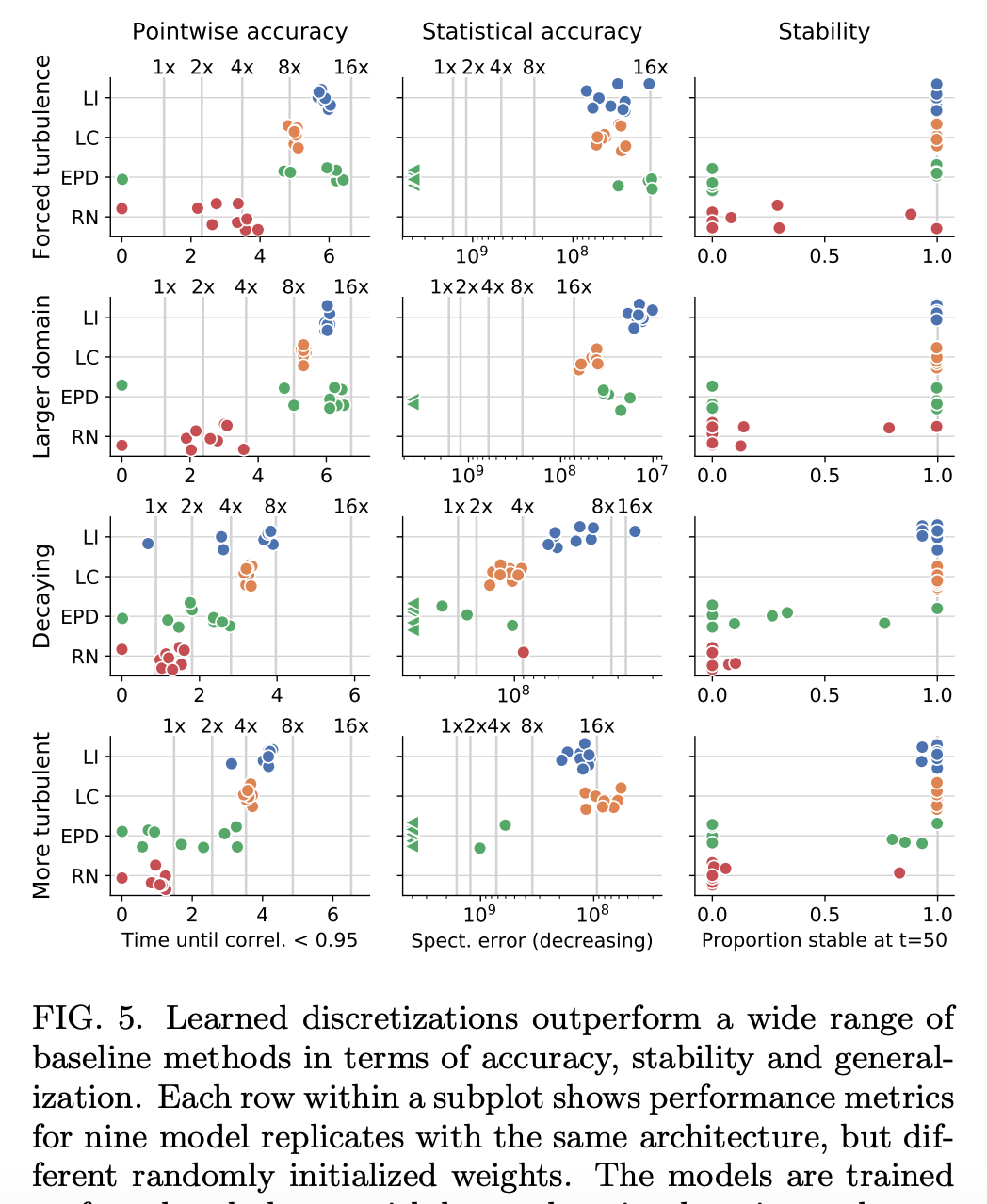
與其他 ML 模型進行對比 研究者將 learned interpolation 與其他 ML 方法的性能進行了對比，包括 ResNet (RN) [50]、Encoder Processor-Decoder (EPD) [51, 52] 架構(gòu)和之前介紹的 learned correction (LC) 模型。下圖 5 展示了這些方法在所有考慮配置中的結(jié)果。總體而言，learned interpolation (LI) 性能最佳，learned correction (LC) 緊隨其后。

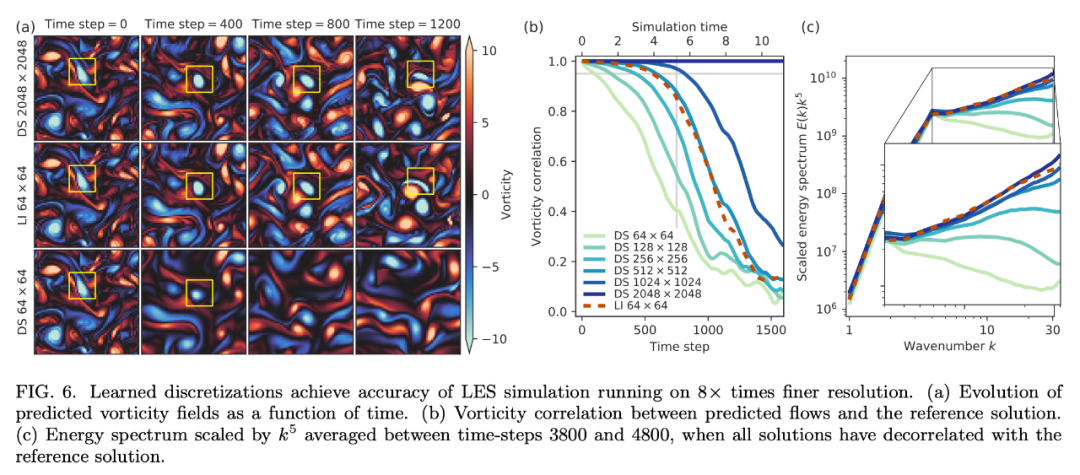
對 LES 的加速效果 研究者已經(jīng)描述了該方法在 DNS 納維 - 斯托克斯方程中的應(yīng)用，但其實該方法是較為通用的，可用于任意非線性偏微分方程。為了證明這一點，研究者將該方法應(yīng)用于 LES 加速。當(dāng) DNS 不可用時，LES 是執(zhí)行大規(guī)模模擬的行業(yè)標(biāo)準(zhǔn)方法。 下圖 6 表明，將 learned interpolation 應(yīng)用于 LES 也能達到 8 倍的 upscaling，相當(dāng)于實現(xiàn)大約 40 倍的加速。

原文標(biāo)題：谷歌AI利用「ML+TPU」實現(xiàn)流體模擬數(shù)量級加速

文章出處：【微信公眾號：深度學(xué)習(xí)實戰(zhàn)】歡迎添加關(guān)注！文章轉(zhuǎn)載請注明出處。

責(zé)任編輯：haq