讀完本文,可以去力扣解決如下題目:
895.最大頻率棧(Hard)
我個人很喜歡設計特殊數據結構的問題,畢竟在工作中會經常用到基本數據結構,而設計類的問題就非常考驗對基本數據結構的理解和運用。
力扣第 895 題要求我們實現一個特殊的數據結構「最大頻率棧」,比較有意思,讓我們實現下面這兩個 API:
class FreqStack {
// 在棧中加入一個元素 val
public void push(int val) {}
// 從棧中刪除并返回出現頻率最高的元素
// 如果頻率最高的元素不止一個,
// 則返回最近添加的那個元素
public int pop() {}
}
比如下面這個例子:
FreqStack stk = new FreqStack();
// 向最大頻率棧中添加元素
stk.push(2); stk.push(7); stk.push(2);
stk.push(7); stk.push(2); stk.push(4);
// 棧中元素:[2,7,2,7,2,4]
stk.pop() // 返回 2
// 因為 2 出現了三次
// 棧中元素:[2,7,2,7,4]
stk.pop() // 返回 7
// 2 和 7 都出現了兩次,但 7 是最近添加的
// 棧中元素:[2,7,2,4]
stk.pop() // 返回 2
// 棧中元素:[2,7,4]
stk.pop() // 返回 4
// 棧中元素:[2,7]
這種設計數據結構的問題,主要是要搞清楚問題的難點在哪里,然后結合各種基本數據結構的特性,高效實現題目要求的 API。
那么,我們仔細思考一下 push 和 pop 方法,難點如下:
1、每次 pop 時,必須要知道頻率最高的元素是什么。
2、如果頻率最高的元素有多個,還得知道哪個是最近 push 進來的元素是哪個。
為了實現上述難點,我們要做到以下幾點:
1、肯定要有一個變量 maxFreq 記錄當前棧中最高的頻率是多少。
2、我們得知道一個頻率 freq 對應的元素有哪些,且這些元素要有時間順序。
3、隨著 pop 的調用,每個 val 對應的頻率會變化,所以還得維持一個映射記錄每個 val 對應的 freq。
綜上,我們可以先實現 FreqStack 所需的數據結構:
class FreqStack {
// 記錄 FreqStack 中元素的最大頻率
int maxFreq = 0;
// 記錄 FreqStack 中每個 val 對應的出現頻率,后文就稱為 VF 表
HashMap《Integer, Integer》 valToFreq = new HashMap《》();
// 記錄頻率 freq 對應的 val 列表,后文就稱為 FV 表
HashMap《Integer, Stack《Integer》》 freqToVals = new HashMap《》();
}
其實這有點類似前文 手把手實現 LFU 算法,注意 freqToVals 中 val 列表用一個棧實現,如果一個 freq 對應的元素有多個,根據棧的特點,可以首先取出最近添加的元素。
要記住在 push 和 pop 方法中同時修改 maxFreq、VF 表、FV 表,否則容易出現 bug。
現在,我們可以來實現 push 方法了:
public void push(int val) {
// 修改 VF 表:val 對應的 freq 加一
int freq = valToFreq.getOrDefault(val, 0) + 1;
valToFreq.put(val, freq);
// 修改 FV 表:在 freq 對應的列表加上 val
freqToVals.putIfAbsent(freq, new Stack《》());
freqToVals.get(freq).push(val);
// 更新 maxFreq
maxFreq = Math.max(maxFreq, freq);
}
pop 方法的實現也非常簡單:
public int pop() {
// 修改 FV 表:pop 出一個 maxFreq 對應的元素 v
Stack《Integer》 vals = freqToVals.get(maxFreq);
int v = vals.pop();
// 修改 VF 表:v 對應的 freq 減一
int freq = valToFreq.get(v) - 1;
valToFreq.put(v, freq);
// 更新 maxFreq
if (vals.isEmpty()) {
// 如果 maxFreq 對應的元素空了
maxFreq--;
}
return v;
}
這樣,兩個 API 都實現了,算法執行過程如下:
嗯,這道題就解決了,Hard 難度的題目也不過如此嘛~
原文標題:數據結構基本功:設計最大頻率棧
文章出處:【微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
數據
+關注
關注
8文章
6909瀏覽量
88850 -
API
+關注
關注
2文章
1487瀏覽量
61833
原文標題:數據結構基本功:設計最大頻率棧
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
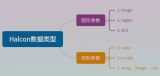
視覺軟件HALCON的數據結構
永磁發電機的主要結構設計是什么?
嵌入式常用數據結構有哪些
5針M16接口結構設計

3針M5插座結構設計

FPGA設計中,對SPI進行參數化結構設計
7芯M9插頭需采用彈性結構設計嗎





 如何解決數據結構設計最大頻率棧問題?
如何解決數據結構設計最大頻率棧問題?











評論