0 引言
路徑規劃是車載導航系統的基本功能,由于其有較強的應用價值,國內外學者對此進行了深入的研究[1-3]。現今較流行的算法有Dijstra算法(簡稱D算法)和A*算法,但D算法搜索速度較慢,A*算法搜索速度快但成功率不高,且這些算法只能在靜態地圖上進行路徑規劃,沒有考慮實時變化的交通狀況。
近年來,智能算法因其強大的搜索能力而被廣泛應用于路徑規劃中。楊易[4]把遺傳算法與A*算法相結合,提高路徑規劃算法的效率;王健[5]把蟻群算法應用到導航的路徑規劃中,但其沒有考慮隨時間的動態變化因素;于海璁等人[6]提出了一種適用于多模式路徑規劃的遺傳算法,可用于個性化的路徑導航。本文將PSO算法應用到車載導航的路徑規劃中,引入變異算子解決PSO算法的局部最優問題,不僅擁有較快的收斂速度,還能增強全局搜索能力。
1 粒子群算法的描述
粒子群算法由Eberhart博士和Kennedy博士在1995年提出[7],它通過粒子間的協作和信息共享來尋找最優解。算法在搜索時,根據粒子自身歷史的最佳位置pbest和種群內所有粒子歷史的最佳位置gbest的基礎上進行位置變化,其速度和位置公式如下:
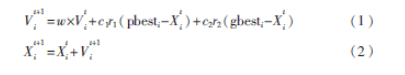
其中,t表示迭代次數,r1、r2是(0,1)之間的隨機數,c1、c2為學習因子,w為慣性權重,其表達式為:

其中wmax、wmin為權重的最大和最小值,tmax為最大迭代次數。
2 粒子群算法在路徑規劃中的應用
本章節的主要內容是解決粒子的編碼和適應度函數的構造,編碼方式涉及粒子位置和速度的更新操作,適應度函數用來評價粒子的適應值。最后還解決了PSO算法自身陷入局部最優的問題。
2.1 粒子編碼
編碼即粒子位置的表達方式,是設計粒子群優化和應用操作的關鍵問題,根據路徑規劃的實際情況,本文采用直觀、方便的實數編碼[8]。粒子狀態表達方式如式(4)所示,編碼方式如式(5)所示。
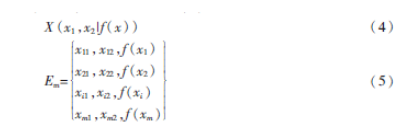
其中,f(x)表示適應值,m表示粒子個數。
2.2 適應度函數
2.2.1 適應度函數的設計
將粒子群算法用于路徑規劃時,適應度函數的設計使得該算法不僅能夠在靜態網絡下獲得最優路徑,通過增加懲罰項M[9]也能適用于實時變化的交通狀況,其適應度函數定義為:

(1)當0
(2)當0.5≤n<0.75時,微擁擠狀態;
(3)當0.75≤n≤1時,嚴重擁堵狀態。
針對不同的擁堵狀態采用不同的適應度函數。
適應度函數主要取決于是否有交通擁堵等狀況,車載導航儀[10]將接收到的交通信息轉換成路段的相關特性數據,同時給出交通擁堵系數n,并根據n的大小選擇相應的適應度函數。采用該適應度函數的優點是占用的存儲空間少,并根據實時的交通狀況找出最佳路徑。
2.2.2 適應度函數對路徑規劃的影響

如圖1所示,粒子群的起點為S,終點為D。粒子群從S點開始搜索,若不定義適應度函數,則粒子隨機選擇移動方向,而根據適應度函數(式(6)),大部分粒子選擇更靠近終點的右方,小部分粒子選擇左方,如圖1(a)所示。當粒子到達下一路口時,重新計算自身適應值,并共享當前全局最優解,各個粒子根據式(1)、(2)更新自身的速度與方向。因此,在單位時間段內,沿著上方行走的粒子數量高于其他方向的粒子數,同時這些粒子記錄自身的局部最優解,也能得到全局最優解。后續粒子選擇路徑時會受這些最優解的影響,沿著粒子較多的方向前進,也有小部分粒子會選擇其他方向來尋求更短的路徑,如圖1(b)所示。當某個粒子到達終點時,其他粒子將會收到該粒子共享的信息,所有粒子將會朝該方向前進,如圖1(c)所示。
2.3 解決陷入“局部最優”的問題
為了避免PSO陷入“局部最優”,本文在PSO算法中引入變異算子,其思想是:當算法達到特定的迭代次數h之后,除去之前擁有全局最優解的粒子外,計算其他粒子與當前全局最優值gbest的距離,若距離小于閾值,則取這些粒子的百分比重新初始化,使這部分粒子重新尋找最優值,使種群獲得更高的粒子多樣性,擴大搜索范圍,避免粒子群算法陷入局部最優,同時能夠增強全局搜索能力。帶變異算子的粒子群算法如下:
If(th)
取滿足dp-gbest
Else
按式(1)、(2)更新粒子速度和位置;
End
其中,t為當前迭代次數,tmax為最大迭代次數,h為特定的迭代次數,dp-gbest表示粒子的當前點到全局最優解gbest的距離,DistValue為設定的距離值。
3 算法驗證與分析
為了驗證上述算法的可行性,本文根據上海市松江區部分實際地圖抽象得到的路網數據結構進行實驗,如圖2所示。
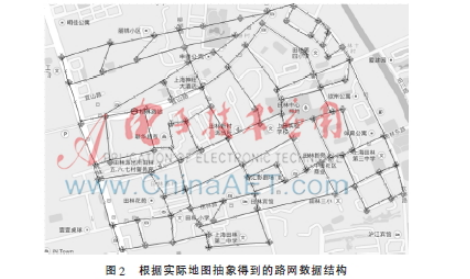
其中路段數為134,路口數為92,粒子數為95,最大迭代次數為200,wmax=0.9,wmin=0.4,c1=c2=2。最優路徑標準采用最短路徑,PSO算法的路徑規劃結果如圖3所示,D算法路徑規劃的結果如圖4所示。

由圖3和圖4可知,D算法規劃出的最優路徑與粒子群算法的最優路徑是一樣的,但兩個算法的搜索時間不同,D算法搜索時間為46 ms,粒子群算法搜索時間為55 ms。
上述結果是在實際地圖上進行的小規模節點數的實驗,圖5和圖6是對大規模節點數進行仿真的結果比較。
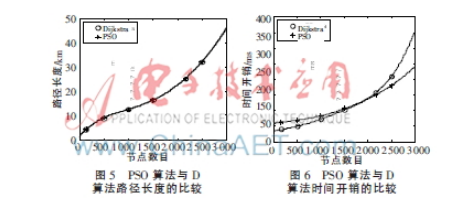
由圖5可知,PSO算法和D算法在節點數相當的情況下,算法求得的路徑長度是相同或相似的,但由圖6可知,由于D算法與PSO算法的原理和收斂方式不同,在節點數目較少時,PSO算法需要更多的時間,但是隨著節點數目的增加,PSO算法的收斂速度較D算法明顯要快,在大規模路網中,PSO算法具有較大優勢。

最后當在路段中設置嚴重交通擁堵,即0.75≤n≤1時,其路徑規劃的結果如圖7所示。
由圖7可知,當在道路上設置擁堵路段時,算法重新規劃出了一條避開擁堵路段的最優路徑,相比于只能夠運用在靜態路網的D算法,該算法更具有實際意義。
4 結論
本文將粒子群算法用于路徑規劃中,從粒子的編碼規則到適應度函數的設計,再到解決局部最優問題等,充分體現了本文的創新性技術,為路徑規劃算法提供了新的研究思路。實驗結果表明,該算法切實可行,其搜索效率高,時間開銷隨路網規模的擴大增幅較小,適用于大規模路網,同時在實時變化的交通路況中更具有實際意義。
參考文獻
[1] 岳雙.動態路徑規劃算法在車輛導航領域中的應用[J].數字技術與應用,2012(3):95-96.
[2] 殷超.基于改進Dijkstra算法的最短路徑搜索仿真[J].山東理工大學學報(自然科學版),2011,24(6):33-36.
[3] 張仁平,周慶忠,熊偉,等.A*算法改進算法及其應用[J].計算機系統應用,2009(9):98-100,107.
[4] 楊易.智能車輛組合定位與路徑導航技術研究[D].長沙:湖南大學,2007.
[5] 王健.基于蟻群算法的車輛導航自適應路徑規劃算法研究[D].青島:青島科技大學,2011.
[6] 于海璁,陸鋒.一種基于遺傳算法的多模式多標準路徑規劃方法[J].測繪學報,2014,43(1):89-96.
[7] 唐小勇,于飛,潘洪悅.改進粒子群算法的潛器導航規劃[J].智能系統學報,2010,5(5):443-448.
[8] 史輝.車載導航路徑規劃算法研究[D].鄭州:解放軍信息工程大學,2010.
[9] 李淑紅,張巧榮.二進制粒子群算法在路徑規劃中的應用[J].計算機工程與設計,2009,30(21):4953-4955.
[10] 孫海鵬,翟傳潤,戰興群,等.基于實時交通信息的動態路徑規劃技術[J].微計算機信息,2007,23(8-3):177-178.
編輯:jq
-
車載導航
+關注
關注
3文章
77瀏覽量
18586 -
PSO
+關注
關注
0文章
49瀏覽量
12921
發布評論請先 登錄
相關推薦
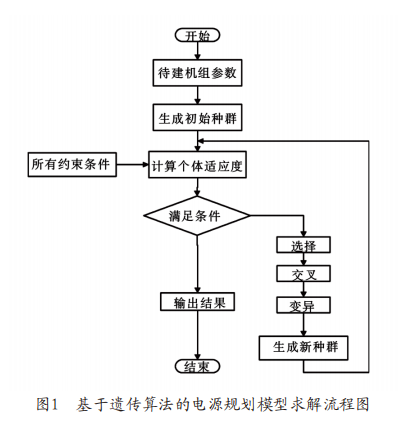
淺談基于儲能電站提高風電消納能力的電源規劃研究
AGV系統設計解析:布局-車體-對接-數量計算-路徑規劃

【Vision Board創客營連載體驗】基于RA8D1-Vision Board的自動路徑規劃小車
基于VPLC711的曲面外觀檢測XYR運動控制解決方案
晶眾地圖華中區銷售總監黃俊赴武漢規劃研究院開展TIM軟件交流培訓
NVIDIA路徑優化引擎創下23項世界紀錄
淺談電動車智能充電設計及研究
淺談智能卡遠程費控電能表的設計與應用研究分析
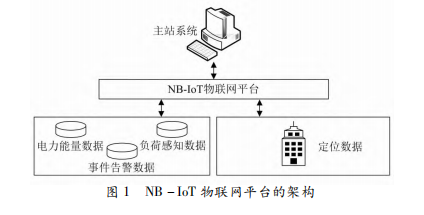
淺談無線測溫系統在電廠的研究和應用

自主機器人近距離操作運動路徑規劃算法




 淺談關于PSO算法路徑規劃的研究
淺談關于PSO算法路徑規劃的研究













評論