混沌系統(tǒng)的控制和同步是當前自然科學基礎研究的熱門課題,它在通信、信息科學、醫(yī)學、生物、工程等領域得到了廣泛的應用,各種控制和同步方法也應運而生。在混沌控制研究中,追蹤問題是研究的一個熱點。追蹤問題即通過施加控制使受控系統(tǒng)的輸出信號達到事先給定的參考信號,更具有一般性。特別是,如果追蹤的參考信號是由混沌系統(tǒng)產生的,這種追蹤控制便演化成為驅動系統(tǒng)和響應系統(tǒng)的同步,它包括自同步和異結構同步,這方面的工作已經有了許多研究。電網之間的互聯(lián)是現(xiàn)代電力系統(tǒng)發(fā)展的必然趨勢,它將使電網的發(fā)電和輸電變得更經濟、更高效。與此同時,電力系統(tǒng)運行的穩(wěn)定性受到前所未有的挑戰(zhàn)。隨著分岔、混沌理論在電力系統(tǒng)非線性動力學行為研究中的應用,人們發(fā)現(xiàn)電力系統(tǒng)中除了低頻振蕩外,還存在混沌振蕩。這種振蕩不僅對系統(tǒng)的穩(wěn)定具有極強的破壞力,而且不能依靠附加傳統(tǒng)的勵磁控制器來抑制或消除。自20世紀90年代以來,國內外許多研究人員對電力系統(tǒng)的分岔、混沌振蕩產生機理進行了充分、有益的探討,但對電力系統(tǒng)混沌控制方法的研究尚屬少見。在此針對變形耦合發(fā)電機昆沌系統(tǒng)的結構特點,并基于非線性系統(tǒng)的線性化穩(wěn)定理論,設計了一個統(tǒng)一形式的非線性追蹤控制器,可以實現(xiàn)變形耦合發(fā)電機系統(tǒng)的狀態(tài)變量與任意給定參考信號的廣義同步。該控制器簡單、易于實現(xiàn)。
1 系統(tǒng)模型
耦合發(fā)電機系統(tǒng)由一個具有混沌特征的三維自治方程組來描述,它是由連接在一起的2臺發(fā)電機組成,其中任何一臺發(fā)電機都處于另一臺發(fā)電機產生的電流所形成的磁場之中。文獻在基于耦合發(fā)電機系統(tǒng)的基礎上,給出了變形耦合發(fā)電機系統(tǒng):
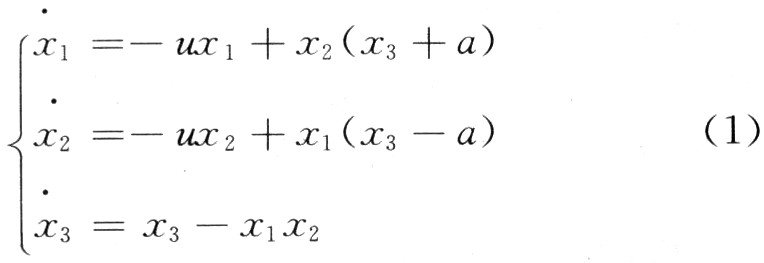
式(1)中,u和a是正的控制參數(shù),當u=2和a=1時系統(tǒng)出現(xiàn)混沌行為。圖1所示為系統(tǒng)1的典型混沌吸引子。由圖可見,系統(tǒng)1的混沌吸引子除具有低維混沌吸引子的一般特點外,還具有其獨特之處;吸引子的二維投影具有更復雜的折疊和拉伸軌線。這說明系統(tǒng)1在局部上比低維混沌系統(tǒng)具有更強的不穩(wěn)定性。這使得對系統(tǒng)1的控制難度大大增加。

2 控制器的設計
對系統(tǒng)1施加控制,使系統(tǒng)的狀態(tài)變量xi(i=1,2,3)追蹤給定參考信號,受控后的系統(tǒng)方程為:

不論參考信號的形式如何,設計如下統(tǒng)一形式的控制器:

式中,r1,r2,r3為給定參考信號。
定理 對于受控系統(tǒng)2,當采用式(3)所示的控制器時,系統(tǒng)狀態(tài)變量xi(i=1,2,3)可以追蹤任意連續(xù)可微的參考信號ri(i=1,2,3)。
證明 設追蹤誤差變量為ei=xi一ri(i=1,2,3),結合式(2)和式(3),可得追蹤誤差系統(tǒng)為:
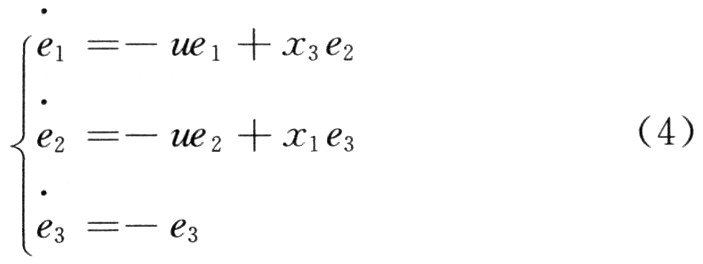
式(4)的平衡點為(0,O,O)。由式(4)可知,誤差變量的零點即為誤差系統(tǒng)的平衡點。式(4)在平衡點處的Ja—cobian陣為:
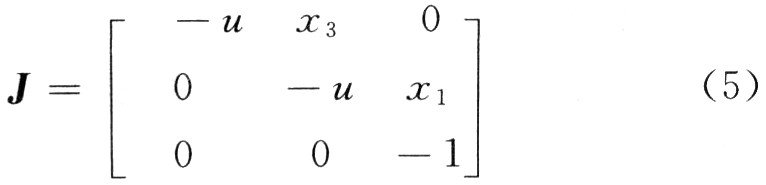
特征方程為:(λ+u)(λ+u)(λ+1)=O,可解得矩陣J的特征根為λ1=一u,λ2=一u,λ2=一l,由于參數(shù)“為正,所以矩陣J的所有特征根均為負數(shù)。由非線性系統(tǒng)的線性化穩(wěn)定理論,誤差系統(tǒng)的零解漸近穩(wěn)定。即lim|ei|=0。
3 數(shù)值仿真
3.1 追蹤常值信號
系統(tǒng)1有5個平衡點,分別為S0(0,0,0),S1(1.175 6,一1.902 1,一2.236 1),S2(一1.175 6,1.902 1,一2.236 1),S3,4(±1.902 1,±1.175 6,2.236 1)。取參考信號為系統(tǒng)平衡點S1,即r1=1.175 6,r2=一1.902 1,r3=一2.236 1。由式(3)得控制器為:
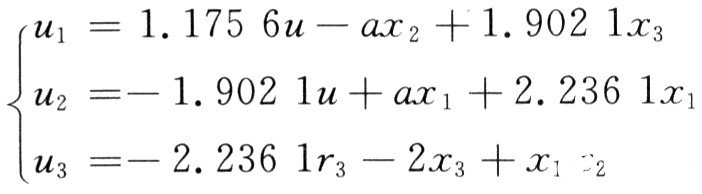
采用四階龍格庫塔法進行數(shù)值仿真,系統(tǒng)2的初值為(0.02,0.006,O.001),仿真步長為0.01,仿真結果如圖2所示。由圖可知,系統(tǒng)變量x(t)經6 s后追蹤上給定的常值參考信號,廣義同步誤差穩(wěn)定在零值處。
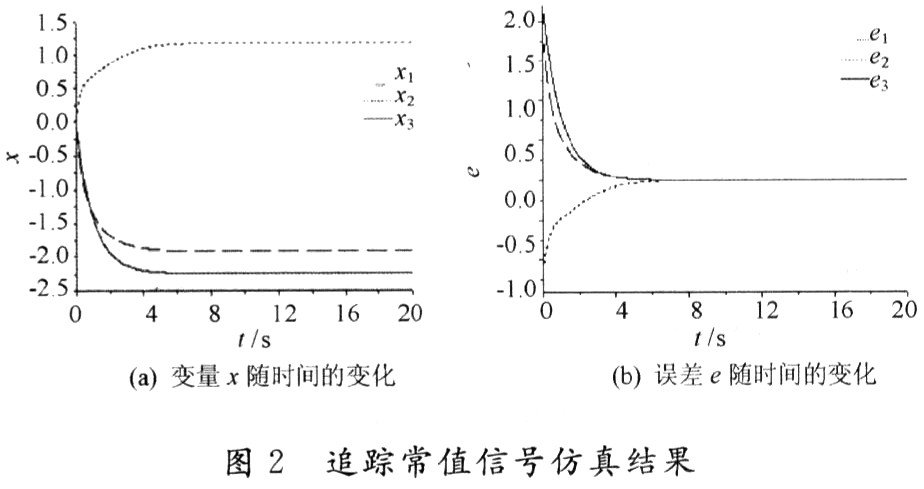
3.2 追蹤周期信號
取參考信號為正弦周期信號r1=sin 4t,r2=cos 2t,r3=sin t,此時控制器為:

同樣采用四階龍格庫塔法進行數(shù)值仿真,系統(tǒng)2的初值為(O.02,O.006,O.001),仿真步長為0.01,仿真結果如圖3所示。由圖可知,變量x1(t),x2(t)和x3(t)在2 s前追蹤上參考信號,而廣義同步誤差e(t)穩(wěn)定在零值附近。
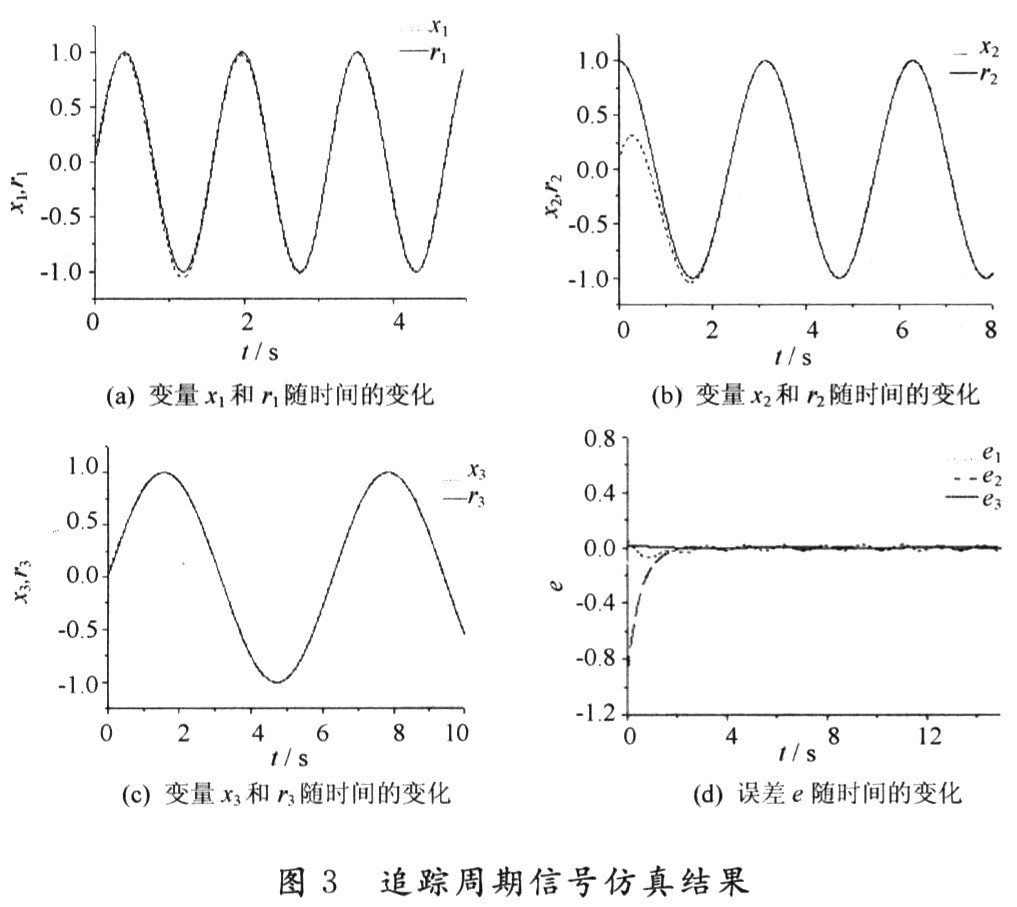
3.3 追蹤混沌信號
Lorenz系統(tǒng)是一個典型的混沌系統(tǒng),其系統(tǒng)方程為:

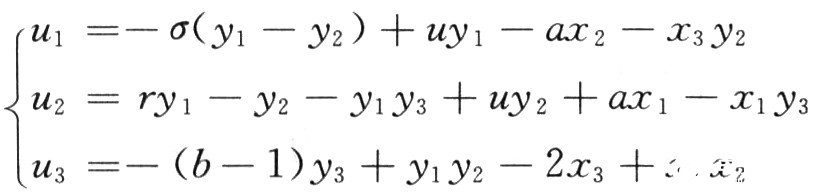
系統(tǒng)2的初值為(O.02,0.006,O.001),Lorenz系統(tǒng)的初值為(O.2,O.07,0.1),仿真步長為0.01,仿真結果如圖4所示。由圖可知,變量x1(t),x2(t)和x3(t)在7 s前追蹤上參考信號,廣義同步誤差e(t)穩(wěn)定在零值處。
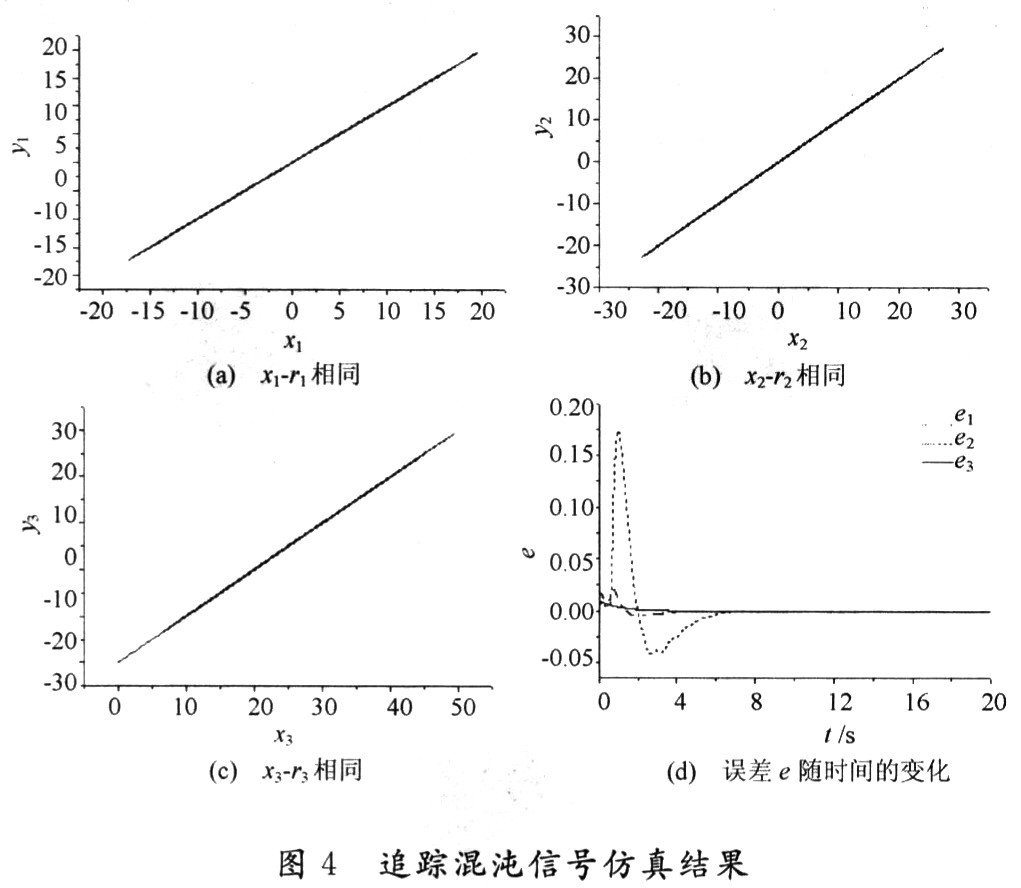
4 結 語
針對變形耦合發(fā)電機混沌系統(tǒng)的結構特點,并基于非線性系統(tǒng)的線性化穩(wěn)定理論,設計了一個統(tǒng)一形式的非線性追蹤控制器。該控制器可以實現(xiàn)變形耦合發(fā)電機系統(tǒng)的狀態(tài)變量與任意給定參考信號的廣義同步,分別以常值信號,周期信號和混沌信號為參考信息進行了數(shù)值仿真,仿真結果與理論分析一致。設計的控制器使用范圍很廣,在控制混沌和利用混沌系統(tǒng)進行數(shù)字保密通信方面有很廣的應用前景。
責任編輯:gt
-
控制器
+關注
關注
112文章
16214瀏覽量
177485 -
發(fā)電機
+關注
關注
26文章
1619瀏覽量
67549
發(fā)布評論請先 登錄
相關推薦
風力發(fā)電機組控制技術綜述
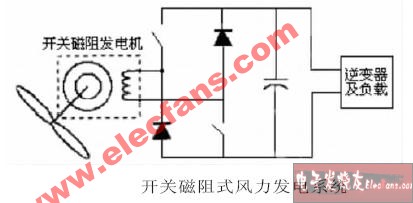
開關磁阻風力發(fā)電機概述
雙繞組感應發(fā)電機實時控制系統(tǒng)的設計
帶整流負載的同步發(fā)電機系統(tǒng)
如何去使用柴油發(fā)電機系統(tǒng)
數(shù)據中心柴油發(fā)電機系統(tǒng)的使用和維護 精選資料分享
柴油發(fā)電機機組的控制器該如何操作
開關磁阻風力發(fā)電機概述
開關磁阻發(fā)電機系統(tǒng)
STATCOM與發(fā)電機勵磁的非線性分散協(xié)調控制

分析變形耦合發(fā)電機混沌系統(tǒng)結構并對追蹤控制器的設計
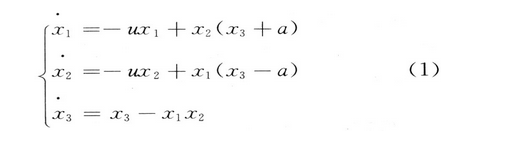
靜音國產發(fā)電機組:靜音型發(fā)電機組控制器是干啥用的?





 基于變形耦合發(fā)電機系統(tǒng)的非線性追蹤控制器的設計
基于變形耦合發(fā)電機系統(tǒng)的非線性追蹤控制器的設計











評論