大家好,又到了每日學習的時間了,上一篇《薦讀:基于FPGA 的CRC校驗碼生成器》文中,提到了“要實現這一過程,仍然需要LFSR電路,參看《FPGA產生基于LFSR的偽隨機數》中關于該電路特性的介紹”,在這補一篇《FPGA產生基于LFSR的偽隨機數》,歡迎大家交流學習。
1.概念
通過一定的算法對事先選定的隨機種子(seed)做一定的運算可以得到一組人工生成的周期序列,在這組序列中以相同的概率選取其中一個數字,該數字稱作偽隨機數,由于所選數字并不具有完全的隨機性,但是從實用的角度而言,其隨機程度已足夠了。這里的“偽”的含義是,由于該隨機數是按照一定算法模擬產生的,其結果是確定的,是可見的,因此并不是真正的隨機數。偽隨機數的選擇是從隨機種子開始的,所以為了保證每次得到的偽隨機數都足夠地“隨機”,隨機種子的選擇就顯得非常重要,如果隨機種子一樣,那么同一個隨機數發生器產生的隨機數也會一樣。
2.由LFSR引出的產生方法
產生偽隨機數的方法最常見的是利用一種線性反饋移位寄存器(LFSR),它是由n個D觸發器和若干個異或門組成的,如下圖:
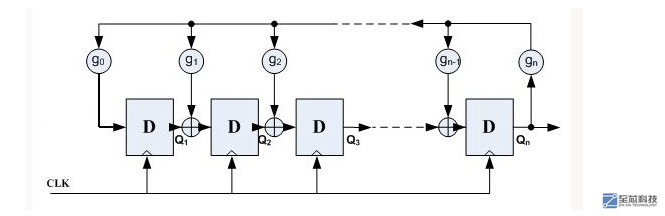
其中,gn為反饋系數,取值只能為0或1,取為0時表明不存在該反饋之路,取為1時表明存在該反饋之路;n個D觸發器最多可以提供2^n-1個狀態(不包括全0的狀態),為了保證這些狀態沒有重復,gn的選擇必須滿足一定的條件。下面以n=3,g0=1,g1=1,g2=0,g3=1為例,說明LFSR的特性,具有該參數的LFSR結構如下圖:
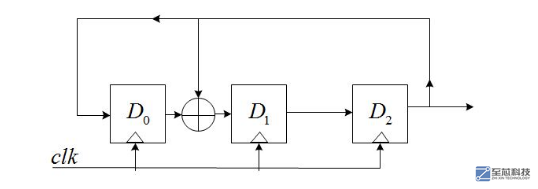
假設在開始時,D2D1D0=111(seed),那么,當時鐘到來時,有:
D2=D1_OUT=1;
D1=D0_OUT^D2_OUT=0;
D0=D2_OUT=1;
即D2D1D0=101;同理,又一個時鐘到來時,可得D2D1D0=001. ………………
畫出狀態轉移圖如下:
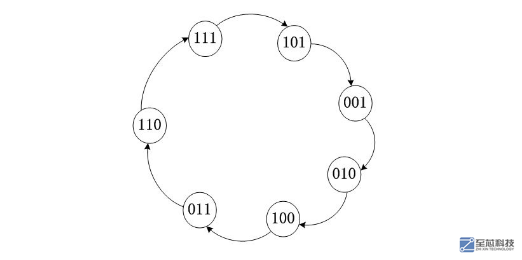
從圖可以看出,正好有2^3-1=7個狀態,不包括全0;
如果你理解了上圖,至少可以得到三條結論:
1)初始狀態是由SEED提供的;
2)當反饋系數不同時,得到的狀態轉移圖也不同;必須保證gn===1,否則哪來的反饋?
3)D觸發器的個數越多,產生的狀態就越多,也就越“隨機”;
3.verilog實現
基于以上原理,下面用verilog產生一個n=8,反饋系數為g0g1g2g3g4g5g6g7g8=101110001的偽隨機數發生器,它共有2^8=255個狀態,該LFSR的結構如下:
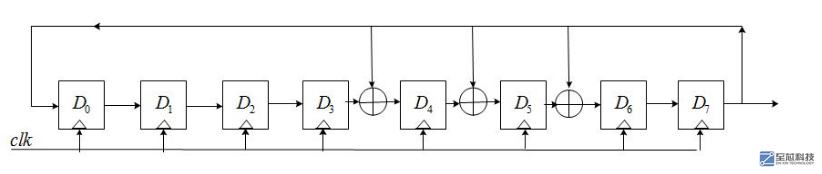
verilog源代碼如下:
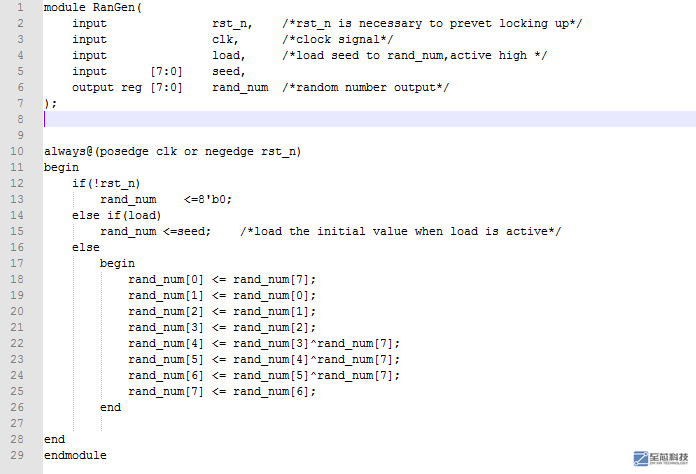
仿真波形:

以1111 1111為種子,load信號置位后,開始在255個狀態中循環,可將輸出值255、143、111……作為偽隨機數。
原文標題:薦讀: FPGA產生基于LFSR的偽隨機數
文章出處:【微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
FPGA
+關注
關注
1626文章
21667瀏覽量
601863 -
LFSR
+關注
關注
0文章
16瀏覽量
12731
原文標題:薦讀: FPGA產生基于LFSR的偽隨機數
文章出處:【微信號:gh_9d70b445f494,微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
藍牙AES+RNG如何保障物聯網信息安全
雅特力AT32 MCU的隨機數生成

全志R128 SDK HAL 模塊開發指南之 TRNG
如何使用Python生成四位隨機數字
合肥硅臻量子芯片通過商密檢測,助力量子芯片商用發展
TC389芯片上HSM的TRNG真隨機數功能,如何判斷其隨機能力呢?
請問rt-thread studio如何使用硬件隨機數生成器?
基于時分復用光學參量振蕩器的5比特全光量子隨機數發生器
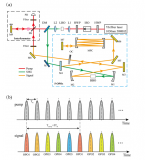
噪聲發生器電路原理圖
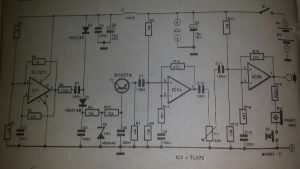
基于FPGA的貪吃蛇游戲設計





 FPGA產生基于LFSR的偽隨機數概念
FPGA產生基于LFSR的偽隨機數概念











評論