1.數字信號處理原理

線性系統中，信號只能以乘以一個常數之后再相加的方式進行組合。例如，一個信號不能直接乘以另外一個信號。如下圖所示，根據給出三個信號：x0［n］，x1［n］，x2［n］相加得到最終的信號x［n］。通過相乘和相加的形式進行信號的組合被稱為信號的合成。

與信號合成相反的步驟，叫做信號的分解。即把原始信號分解為兩個或多個信號相加。信號的分解要比信號合成要復雜些。試想，假設我們把15和25相加，那么我們只能得到40，；相反，如果我們把40分解成兩個或多個數字的相加，那么這種分解會有無數種形式，比如1+39，2+38，-30.5+60+10.5。

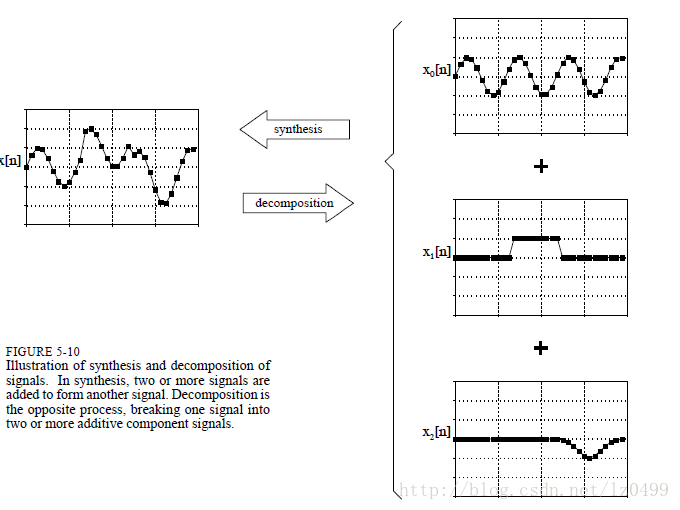
圖1

數字信號處理中，最為關鍵的步驟是信號的疊加。假設有如下圖的輸入信號x［n］，經過一個線性系統之后，輸出信號為y［n］。輸入信號可以分解為多個更為簡單的信號：x1［n］，x2［n］，x3［n］，這些被稱為輸入信號分量。之后把各個輸入信號分量單獨的輸入到線性系統中，產生與之對應的輸出信號分量：y1［n］，y2［n］，y3［n］。原始的輸入信號經過線性系統之后，得到的輸出信號y［n］即為各個輸出信號分量的合成。線性系統中，通過這種方式獲得的輸出信號和原始信號直接通過系統得到的輸出結果是一樣的。正因為如此，任何復雜的數字信號，我們應該把它分解為更為簡單的輸入信號分量，經過線性系統后把輸出信號分量進行合成即為最終的輸出信號。但是，如果分解的輸入信號不夠簡單，那么這樣與分解之前的效果是一樣的，需要復雜的計算。

假設你需要計算2014乘以4的結果，我們可以這樣進行計算：把2014分解為2000+10+4，分解的系數分別乘以4再相加即為最終的輸出結果。這種方法比直接把兩個數相乘要簡單得多。

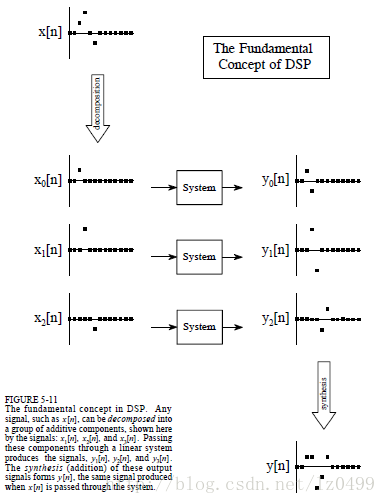
圖2

2.卷積

脈沖分解

脈沖分解是卷積的基礎。如下圖所示，N個采樣信號經過脈沖分解之后，形成N個信號分量，每個信號分量只包含原始信號的某一個采樣點信號，而其他采樣點的值為0。假若某個信號只有一個非零點，其他各點數值均為0，那么這個信號被稱為脈沖信號。

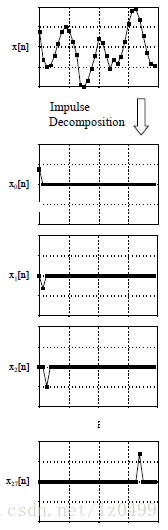
圖3

脈沖函數

Delta函數用希臘字母表示為o［n］。delta 函數是一個歸一化的脈沖信號，即在采樣點零點位置其值為1，其他采樣點位置各點數值均為0。

脈沖反應

當線性系統中輸入信號為delta函數時，其輸出的信號稱為脈沖反應。如下圖所示。如果兩個不同的線性系統，當輸入信號均為delta函數時，其輸出分脈沖反應也是不同的。就像離散數字信號中，用x［n］、y［n］分別表示輸入信號和輸出信號，脈沖反應使用h［n］表示。當然，你也可以使用其他的符號表示，比如f［n］等。

任何脈沖信號都可以看作是脈沖函數的平移和縮放。例如，假設信號a［n］只在采樣點8的位置有輸入，且其輸入值為-3，這就相當于把delta函數平移到8的位置，在乘以-3.用公式表示為：a［n］ = -3 o［n-8］。假如delta函數的脈沖反應為h［n］，那么a［n］的脈沖反應為-3h［n-8］。

卷積就像數學的加減乘除一樣，是一種形式化的數學運算。數學運算中輸入兩個數得到第三個數，卷積則是輸入兩個信號產生第三個信號。卷積被廣泛應用于統計和概率中。在線性系統中，卷積描述的是輸入信號，脈沖反應和輸出信號三者之間的關系。

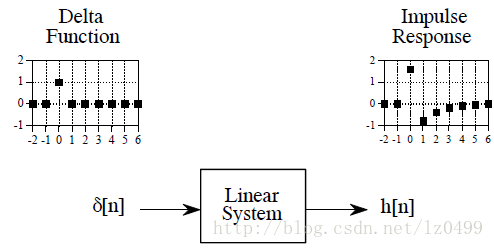
圖4

上圖描述的是卷積應用于線性系統的示意圖。輸入信號x［n］進入有脈沖反應h［n］的線性系統，產生輸出信號y［n］。用公式表示為：x［n］*h［n］ = y［n］。

3.卷積運算

卷積可以從輸入信號的角度理解：輸入信號的每一個采樣點是如何貢獻于多個輸出信號采樣點，即每一個輸入信號分量進入線性系統之后，都將產生多個平移和縮放版本的脈沖反應，輸出結果即為每個信號分量對應的平移和縮放版的脈沖反應進行合成；從輸出信號的角度理解：每一個輸出信號的采樣點是如何從眾多輸入信號采樣點獲取信息。即對于每一個輸出信號，都將由多個輸入信號貢獻其脈沖響應，輸出結果即為對應脈沖響應的線性加權。

這兩個理解只是對卷積運算的不同角度的理解，其結果都是一樣的。

從輸入信號的角度理解

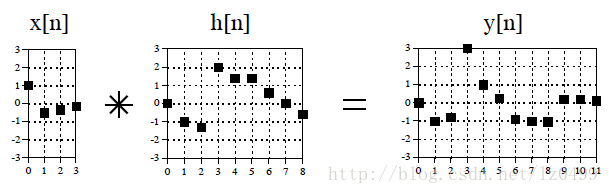
圖5

上圖是一個簡單的卷積計算。輸入信號x［n］有九個點，輸入一個有四個脈沖反應h［n］的線性系統中，得到9+4-1輸出信號y［n］。用數學術語表示為：x［n］卷積h［n］輸出結果y［n］。以第一種角度理解卷積：分解輸入信號，把輸入信號分量通過線性系統，然后把每一個輸出分量進行合成。在這個例子中，輸入信號的每一個采樣點都將產生一個平移和縮放版的脈沖反應，輸出信號即把這些平移和縮放版的脈沖反應疊加生成最終的輸出信號y［n］。其具體的計算過程如下圖所示：

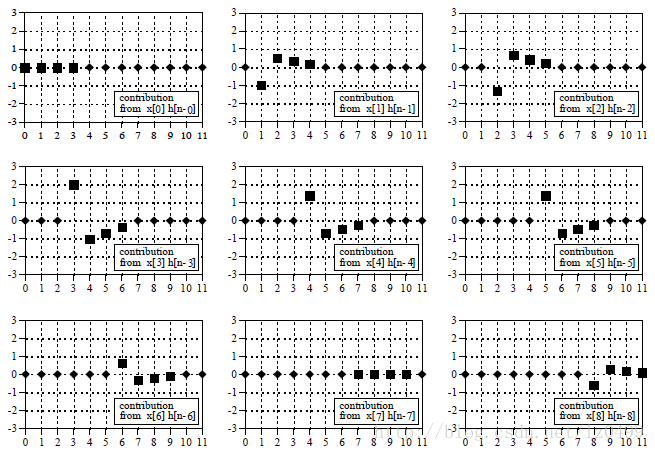
圖6

圖6：輸入信號中的每一個分量都將產生一個平移和縮放版的脈沖反應。即用方形所表示的脈沖反應結果。除了方形之外的所有點起數值均為0.

假設我們從輸入信號的第四個采樣點x［4］開始。這個采樣點的下標為4，其值為1.4。當輸入信號分解之后，這個采樣點可以用脈沖函數表示為：1.4 o［n-4］。經過線性系統之后，該采樣點所對應的輸出信號分量為1.4h［n-4］。如上圖中間位置圖像所示。注意到輸出信號分量脈沖反應乘以1.4，并把采樣點右移到下表為四的采樣點。0-3，8-11各點數值均為0.

上圖中方塊形狀表示的即為平移和縮放的脈沖反應數值，鉆石形狀的點其值為0.

當輸入信號是四個采樣，經過有九個點的脈沖反應線性系統，其輸出的結果與上圖所示的方法結果相同。

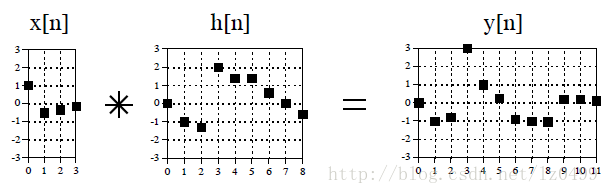
圖7

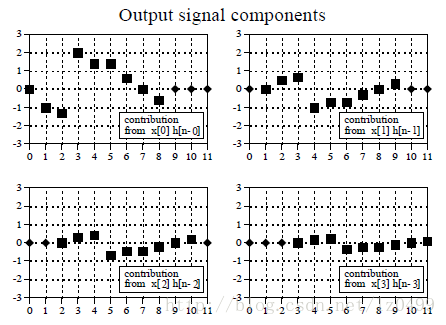
圖8

上述兩種計算方法結果相同，揭示了卷積的一個重要性質：卷積的交換律。即a［n］*b［n］=b［n］*a［n］。即卷積并不關心哪個信號是輸入信號哪個信號是脈沖反應。

假設輸入信號為{1，2，3，4，1，2，3，4，5}；脈沖反應為：{2，3，1，4};則卷積計算過程相當于如下所示，每一個輸入信號分量分解為單個脈沖函數，經過四個點的h［n］線性系統之后，其輸出結果即為h［n］+2*h［n-1］+3*h［n-2］+4*h［n-3］+ h［n-4］+2*h［n-1-5］+3*h［n-6］+4*h［n-7］+5h［n-8］。

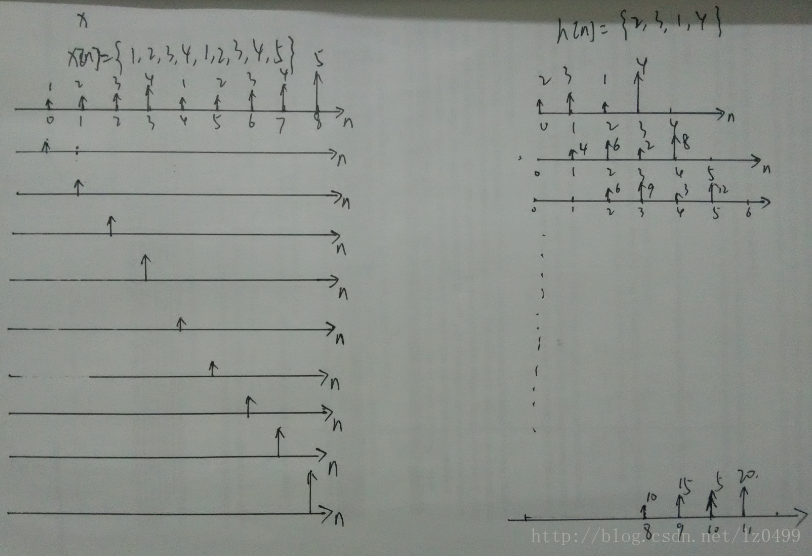
圖9

圖10

從輸入信號角度理解卷積代碼示例：

#include《math.h》#include《stdio.h》#include《stdlib.h》 int main（）{ int InputSignal［9］ = {1，2，3，4，1，2，3，4，5}; int ImpulseCorres［4］ = {2，3，1，4}; int OutPut［12］ = {0}; int i，j; //input view for（i = 0;i 《 9;i++） { for（j = 0;j 《 4;j++） OutPut［i+j］ = OutPut［i+j］+InputSignal［i］*ImpulseCorres［j］; } for（i = 0;i 《 12;i++） { printf（“%d ”，OutPut［i］）; } return 0;}

從輸出信號的角度理解

從輸出信號角度理解卷積，分析的是每一個輸入信號的采樣點是如何影響眾多輸出信號的采樣點。而從輸出角度理解卷積，分析的是輸出信號的每一個采樣點是由哪些輸入信號影響的。這種方式對數學角度和實踐應用角度理解卷積都相當有作用。用公式表示即為：y［n］=其他變量的組合。換句話說，輸出信號采樣點n等于眾多輸入信號和脈沖反應的線性組合。

從如圖6可以看出，單個輸出信號是如何受到眾多輸入型號的影響的。假設我們以y［6］為例，在圖6中找到在n=6的位置，九個輸入信號中有哪些數值為非零的采樣點作用于該位置。由圖可以看出五個輸入信號在n = 6的位置其數值為0，只有四格輸入信號作用于n = 6的時候其數值不為零。分別是x［3］，x［4］，x［5］，x［6］。y［6］的最終結果即為這四個輸入信號作用單獨作用于線性系統的后輸出信號分量之和。即y［6］ = x［3］*h［3］+x［4］*h［2］+x［5］*h［1］+x［6］*h［0］。

圖11，從輸出信號角度理解卷積，其相當于一個卷積機器。如圖所示，假設輸入信號x［n］，輸出信號y［n］， 虛線方框里表示的是卷積機器，可以從左到右從右到左自由移動。卷積機器放置的位置應該與我們需要求得輸出信號采樣點對其，輸入信號的四個采樣點進入到卷積機器，四個采樣點的數字分別于其對應的脈沖反應相乘，再把其乘積相加。例如為了計算y［6］，需要把x［3］，x［4］，x［5］，x［6］四個輸入信號輸送到卷積機器。相應的，為了計算y［7］，卷積機器必須右移一位到采樣點7的位置，這樣，進入到卷積的四個信號分別是x［4］，x［5］，x［6］， x［7］，如此循環直到所有輸出信號分量被計算完成。

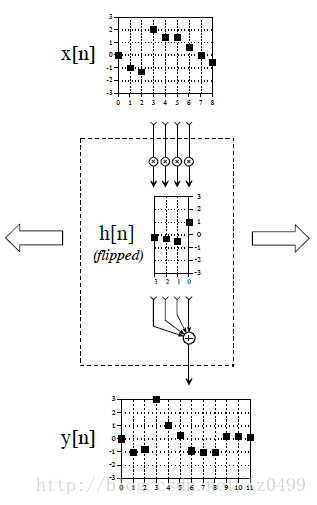
圖11

卷積機器中脈沖反應排列順序是相當重要的。卷積機器中的脈沖反應與原始的脈沖反應做了一個鏡像的翻轉。為什么需要翻轉呢？

即假設我們計算y［4］的輸出結果，由上圖可知y［4］ = x［4］*h［0］+x［3］*h［1］+x［2］*h［2］+x［1］*h［3］+x［0］*h［4］。即當前輸入信號點輸入到線性系統對應的輸出結果是當前信號和之前各個信號對當前點的脈沖反應的一個線性加權。如公式所述，為了計算y［4］的結果，我們必須把輸入x［0］，x［1］，x［2］，x［3］，x［4］作用在n = 4的位置的脈沖響應進行線性加權。也就是說，當x［0］進入系統的時候，在n = 4的位置對應的脈沖反應為h［4］，其輸出為x［0］*h［4］，當x［1］進入系統后，在n = 4的位置對應的脈沖反應為h［3］，其輸出結果為x［1］*h［3］以此類推。由此可以看出，輸出信號的每一個分量都是有收到輸入信號影響的權重線性組合，其權重恰好是脈沖反應的鏡像翻轉對應的權重值。這也就是為什么卷積公式中需要把輸入信號進行翻轉在進行線性疊加的原因。

假設有N個點的輸入信號x［n］，采樣點從0-N-1，有M個點，脈沖反應為h［n］的線性系統，信號點從0-M-1。則這兩個信號的卷積將輸出有N+M-1個采樣點的信號，下標從0-N+M-2。用公式表示為：

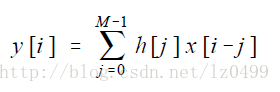
從輸出信號角度理解卷積代碼示例：

#include《math.h》#include《stdio.h》#include《stdlib.h》 int main（）{ int InputSignal［9］ = {1，2，3，4，1，2，3，4，5}; int ImpulseCorres［4］ = {2，3，1，4}; int OutPut［12］ = {0}; int i，j; //output view for（i = 0;i 《 12;i++） { OutPut［i］ = 0; for（j = 0; j 《 4;j++） { if（（i-j）《0） continue; if（（i-j）》8） continue; OutPut［i］ += ImpulseCorres［j］*InputSignal［i-j］; } } for（i = 0;i 《 12;i++） { printf（“%d ”，OutPut［i］）; } return 0; }

4.圖像中的卷積

假設二維函數I和H，對應的卷積操作可以表示為：

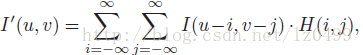
也可以表示為：

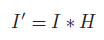
應用于圖像領域時，其卷積公式也可以表示為：

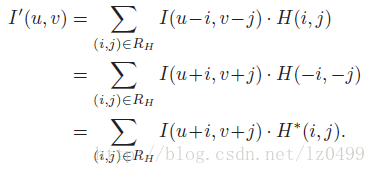
當濾波函數H*（I，j） = H（-I，-j）進，H（I，j）進行了180度旋轉之后，其結果與線性濾波時一樣的。

圖像中的線性濾波可以表示為：

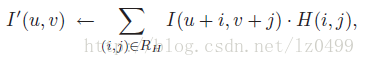
其原理為：

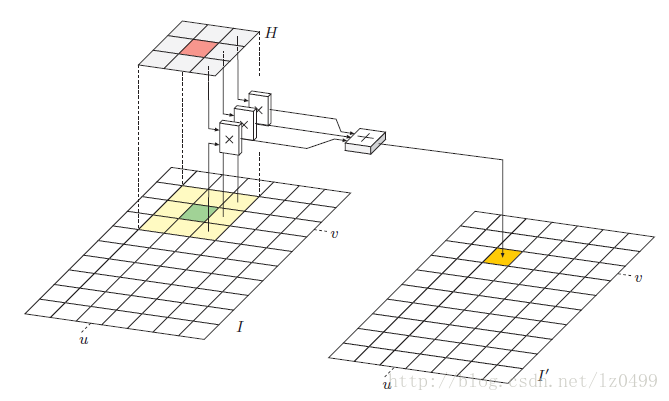
由兩者的公式可以看出，線性濾波其實是把濾波函數進行180度旋轉之后進行卷積的結果。

以待吧！
編輯：lyn