前言性能優化不管是從方法論還是從實踐上都有很多東西,從 C++ 語言本身入手,介紹一些性能優化的方法,希望能做到簡潔實用。
實例1在開始本文的內容之前,讓我們看段小程序:
// 獲取一個整數對應10近制的位數
uint32_t digits10_v1(uint64_t v) {
uint32_t result = 0;
do {
++result;
v /= 10;
} while (v);
return result;
}
如果要對這段代碼進行優化,你認為瓶頸會是什么呢?代碼 -g -O2 后看一眼匯編:
Dump of assembler code for function digits10_v1(uint64_t):
0x00000000004008f0 《digits10_v1(uint64_t)+0》: mov %rdi,%rdx
0x00000000004008f3 《digits10_v1(uint64_t)+3》: xor %esi,%esi
0x00000000004008f5 《digits10_v1(uint64_t)+5》: mov $0xcccccccccccccccd,%rcx
0x00000000004008ff 《digits10_v1(uint64_t)+15》: nop
0x0000000000400900 《digits10_v1(uint64_t)+16》: mov %rdx,%rax
0x0000000000400903 《digits10_v1(uint64_t)+19》: add $0x1,%esi
0x0000000000400906 《digits10_v1(uint64_t)+22》: mul %rcx
0x0000000000400909 《digits10_v1(uint64_t)+25》: shr $0x3,%rdx
0x000000000040090d 《digits10_v1(uint64_t)+29》: test %rdx,%rdx
0x0000000000400910 《digits10_v1(uint64_t)+32》: jne 0x400900 《digits10_v1(uint64_t)+16》
0x0000000000400912 《digits10_v1(uint64_t)+34》: mov %esi,%eax
0x0000000000400914 《digits10_v1(uint64_t)+36》: retq
/*
注:對于常數的除法操作,編譯器一般會轉換成乘法+移位的方式,即
a / b = a * (1/b) = a * (2^n / b) * (1 / 2^n) = a * (2^n / b) 》》 n.
這里的n=3, b=10, 2^n/b=4/5,0xcccccccccccccccd是編譯器對4/5的定點算法表示
*/
指令已經很少了,有多少優化空間呢?先不著急,看看下面這段代碼
uint32_t digits10_v2(uint64_t v) {
uint32_t result = 1;
for (;;) {
if (v 《 10) return result;
if (v 《 100) return result + 1;
if (v 《 1000) return result + 2;
if (v 《 10000) return result + 3;
// Skip ahead by 4 orders of magnitude
v /= 10000U;
result += 4;
}
}
uint32_t digits10_v3(uint64_t v) {
if (v 《 10) return 1;
if (v 《 100) return 2;
if (v 《 1000) return 3;
if (v 《 1000000000000) { // 10^12
if (v 《 100000000) { // 10^7
if (v 《 1000000) { // 10^6
if (v 《 10000) return 4;
return 5 + (v 》= 100000); // 10^5
}
return 7 + (v 》= 10000000); // 10^7
}
if (v 《 10000000000) { // 10^10
return 9 + (v 》= 1000000000); // 10^9
}
return 11 + (v 》= 100000000000); // 10^11
}
return 12 + digits10_v3(v / 1000000000000); // 10^12
}
寫了一個小程序,digits10_v2 比 digits10_v1 快了 45%, digits10_v3 比digits10_v1 快了60%+。不難看出測試結論跟數據的取值范圍相關,就本例來說數值越大,提升越明顯。是什么原因呢?附測試程序:
int main() {
srand(100);
uint64_t digit10_array[ITEM_COUNT];
for( int i = 0; i 《 ITEM_COUNT; ++i )
{
digit10_array[i] = rand();
}
struct timeval start, end;
// digits10_v1
uint64_t sum1 = 0;
uint64_t time1 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i 《 RUN_TIMES; ++i )
{
sum1 += digits10_v1(digit10_array[i]);
}
gettimeofday(&end,NULL);
time1 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v2
uint64_t sum2 = 0;
uint64_t time2 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i 《 RUN_TIMES; ++i )
{
sum2 += digits10_v2(digit10_array[i]);
}
gettimeofday(&end,NULL);
time2 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v3
uint64_t sum3 = 0;
uint64_t time3 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i 《 RUN_TIMES; ++i )
{
sum3 += digits10_v3(digit10_array[i]);
}
gettimeofday(&end,NULL);
time3 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
cout 《《 “sum1:” 《《 sum1 《《 “ sum2:” 《《 sum2 《《 “ sum3:” 《《 sum3 《《 endl;
cout 《《 “cost1:” 《《 time1 《《 “us cost2:” 《《 time2 《《 “us cost3:” 《《 time3 《《 “us”
《《 “ cost2/cost1:” 《《 (1.0*time2)/time1
《《 “ cost3/cost1:” 《《 (1.0*time3)/time1 《《 endl;
return 0;
}
/*
執行結果:
g++ -g -O2 cplusplus_optimize.cpp && 。/a.out
sum1:9944152 sum2:9944152 sum3:9944152
cost1:27560us cost2:14998us cost3:10525us cost2/cost1:0.544194 cost3/cost1:0.381894
*/
Strength reduction
優化原因不是因為做了循環展開,而是由于不同指令本身的速度就是不一樣的,比較、整型的加減、位操作速度都是最快的,而除法/取余卻很慢。下面有一個更詳細的列表,為了更直觀一些,用了clock cycle 來衡量,不過這里的 clock cycle 是個平均值,不同的 CPU 還是稍有差異:
* comparisons (1 clock cycle)
* (u)int add, subtract, bitops, shift (1 clock cycle)
* floating point add, sub (3~6 clock cycle)
* indexed array access (cache effects)
* (u)int32 mul (3~4 clock cycle)
* Floating point mul (4~8 clock cycle)
* Float Point division, remainder (14~45 clock cycle)
* (u)int division, remainder (40~80 clock cycle)
雖然大多數場景下,數學運算都不會有太多性能問題,但相對來說,整型的除法運算還是比較昂貴的。編譯器就會利用這一特點進行優化,一般稱作 Strength reduction.
對于前面的例子,核心原因是 digits10_v2 用比較和加法來減少除法 (/=) 操作,digits10_v3 通過搜索的方式進一步減少了除法操作。由于 cpu 并行處理技術,我們不能簡單的用后面的 clock cycle 來衡量性能,但不難看出處理器對類型的還是非常敏感的,以整型和浮點的處理為例:
整型類型轉換
int--》 short/char (0~1 clock cycle)
int --》 float/double (4~16個clock cycle), signed int 快于 unsigned int,唯一一個場景 signed 比 unsigned 快的
short/char 的計算通常使用 32bit 存儲,只是返回的時候做了截取,故只在要考慮內存大小的時候才使用 short/char,如 array
注:隱式類型轉換可能會溢出,有符號的溢出變成負數,無符號的溢出變成小的整數
運算
除法、取余運算unsigned int 快于 signed int
除以常量比除以變量效率高,因為可以在編譯期做優化,尤其是常量可以表示成2^n時
++i和i++本身性能一樣,但不同的語境效果不一樣,如array[i++]比arry[++i]性能好;當依賴自增結果時,++i性能更好,如a=++b,a和b可復用同一個寄存器
代碼示例
// div和mod效率
int a, b, c;
a = b / c; // This is slow
a = b / 10; // Division by a constant is faster
a = (unsigned int)b / 10; // Still faster if unsigned
a = b / 16; // Faster if divisor is a power of 2
a = (unsigned int)b / 16; // Still faster if unsigned
浮點單精度、雙精度的計算性能是一樣的
常量的默認精度是雙精度
不要混淆單精度、雙精度,混合精度計算會帶來額外的精度轉換開銷,如
// 混用
float a, b;
a = b * 1.2; // bad. 先將b轉換成double,返回結果轉回成float
// Example 14.18b
float a, b;
a = b * 1.2f; // ok. everything is float
// Example 14.18c
double a, b;
a = b * 1.2; // ok. everything is double
浮點除法比乘法慢很多,故可以利用乘法來加快速度,如:
double y, a1, a2, b1, b2;
y = a1/b1 + a2/b2; // slow
double y, a1, a2, b1, b2;
y = (a1*b2 + a2*b1) / (b1*b2); // faster
這里介紹的大多是編譯器的擅長但又不能直接優化的場景,也是平常優化中比較容易忽視的點,其實往往我們往前多走一步,編譯器就可以工作得更好。
實例2先看一個數字轉字符串的例子,stringstream 和 sprintf 自然不會是我們考慮的對象,雖然 protobuf 庫中的 FastInt32ToBuffer 很不錯,其實還能優化,下面的版本就比例子中 stringstream 快 6 倍,代碼如下:
// integer to string
uint32_t u64ToAscii_v1(uint64_t value, char* dst) {
// Write backwards.
char* start = dst;
do {
*dst++ = ‘0’ + (value % 10);
value /= 10;
} while (value != 0);
const uint32_t result = dst - start;
// Reverse in place.
for (dst--; dst 》 start; start++, dst--) {
std::iter_swap(dst, start);
}
return result;
}
不用細讀 stringstream/sprintf 的源碼,反匯編看下就能知道個大概,對于轉字符串這個場景,stringstream/sprintf 就太重了,通常來說越少的指令性能也越好,本文討論的重點是內存訪問,就上面這段代碼,有什么內存使用上的問題?如何進一步優化?
分析
優化前還是得找一下性能熱點,下面是 vtune 結果的截圖(雖然 cpu time 和匯編指令的消耗對應得不是特別好):
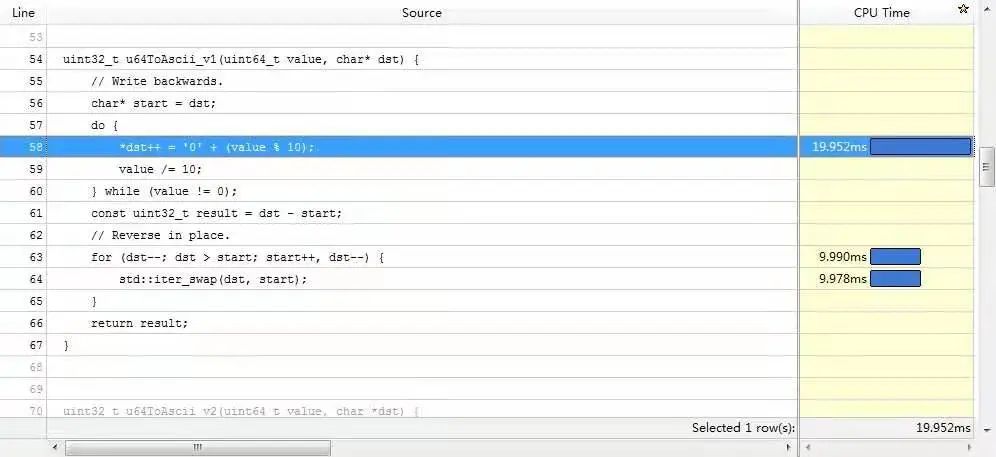
vtune_1
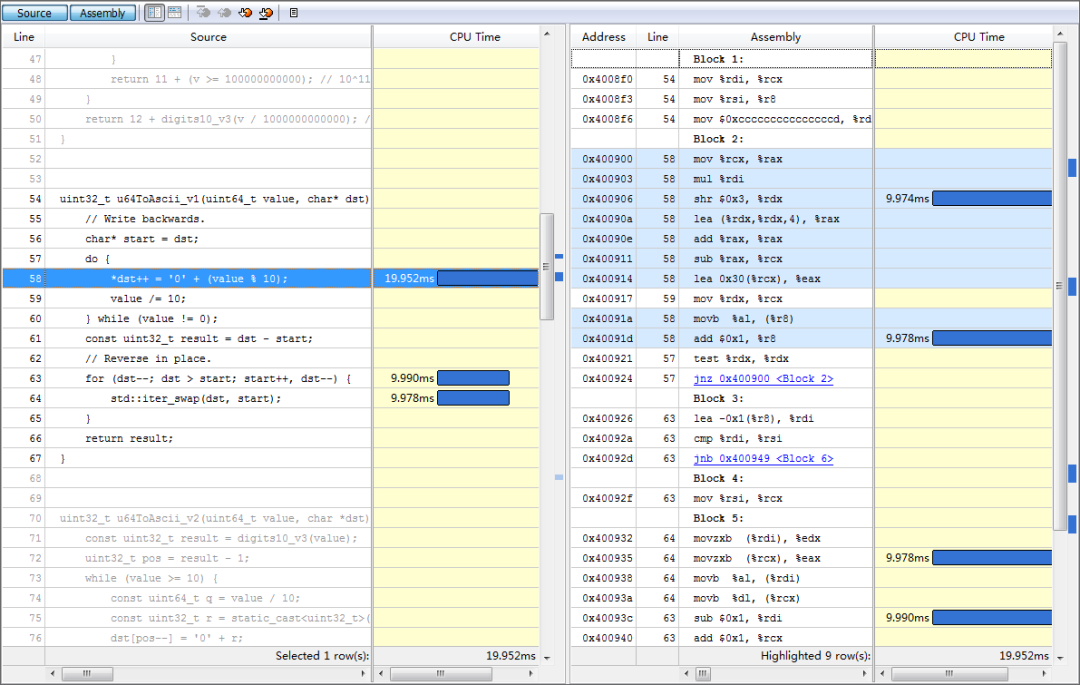
vtune_2
數組 reverse 的開銷跟上面生成數組元素相近,reverse有這么耗時么?
從圖中的匯編可以看出,一次 swap 對應著兩次內存讀 (movzxb)、兩次內存寫 (movb),因為一次寫就意味著一個讀和一個寫,描述的是內存--》cache--》內存的過程。
優化
減少內存寫操作 一個很自然的優化想法,應該盡量避免內存寫操作,于是代碼可以進一步優化,結合 Strength reduction,代碼如下:
uint32_t u64ToAscii_v2(uint64_t value, char *dst) {
const uint32_t result = digits10_v3(value);
uint32_t pos = result - 1;
while (value 》= 10) {
const uint64_t q = value / 10;
const uint32_t r = static_cast《uint32_t》(value % 10);
dst[pos--] = ‘0’ + r;
value = q;
}
*dst = static_cast《uint32_t》(value) + ‘0’;
return result;
}
實測發現新版本比之前版本性能提升了 10%,還有優化空間么?答案是,有。方案是:通過查表,一次處理2個數字,減少數據依賴,如:
uint32_t u64ToAscii_v3(uint64_t value, char* dst) {
static const char digits[] =
“0001020304050607080910111213141516171819”
“2021222324252627282930313233343536373839”
“4041424344454647484950515253545556575859”
“6061626364656667686970717273747576777879”
“8081828384858687888990919293949596979899”;
const size_t length = digits10_v3(value);
uint32_t next = length - 1;
while (value 》= 100) {
const uint32_t i = (value % 100) * 2;
value /= 100;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
next -= 2;
}
// Handle last 1-2 digits
if (value 《 10) {
dst[next] = ‘0’ + uint32_t(value);
} else {
uint32_t i = uint32_t(value) * 2;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
}
return length;
}
結論:
u64ToAscii_v3性能比基準版本提升了30%;
如果用到悟時的那個測試場景,性能可以提升6.5倍。
下面是完整的測試代碼和結果:
#include 《sys/time.h》
#include 《iostream》
#define ITEM_COUNT 1024*1024
#define RUN_TIMES 1024*1024
#define BUFFERSIZE 32
using namespace std;
uint32_t digits10_v1(uint64_t v) {
uint32_t result = 0;
do {
++result;
v /= 10;
} while (v);
return result;
}
uint32_t digits10_v2(uint64_t v) {
uint32_t result = 1;
for(;;) {
if (v 《 10) return result;
if (v 《 100) return result + 1;
if (v 《 1000) return result + 2;
if (v 《 10000) return result + 3;
v /= 10000U;
result += 4;
}
return result;
}
uint32_t digits10_v3(uint64_t v) {
if (v 《 10) return 1;
if (v 《 100) return 2;
if (v 《 1000) return 3;
if (v 《 1000000000000) { // 10^12
if (v 《 100000000) { // 10^7
if (v 《 1000000) { // 10^6
if (v 《 10000) return 4;
return 5 + (v 》= 100000); // 10^5
}
return 7 + (v 》= 10000000); // 10^7
}
if (v 《 10000000000) { // 10^10
return 9 + (v 》= 1000000000); // 10^9
}
return 11 + (v 》= 100000000000); // 10^11
}
return 12 + digits10_v3(v / 1000000000000); // 10^12
}
uint32_t u64ToAscii_v1(uint64_t value, char* dst) {
// Write backwards.
char* start = dst;
do {
*dst++ = ‘0’ + (value % 10);
value /= 10;
} while (value != 0);
const uint32_t result = dst - start;
// Reverse in place.
for (dst--; dst 》 start; start++, dst--) {
std::iter_swap(dst, start);
}
return result;
}
uint32_t u64ToAscii_v2(uint64_t value, char *dst) {
const uint32_t result = digits10_v3(value);
uint32_t pos = result - 1;
while (value 》= 10) {
const uint64_t q = value / 10;
const uint32_t r = static_cast《uint32_t》(value % 10);
dst[pos--] = ‘0’ + r;
value = q;
}
*dst = static_cast《uint32_t》(value) + ‘0’;
return result;
}
uint32_t u64ToAscii_v3(uint64_t value, char* dst) {
static const char digits[] =
“0001020304050607080910111213141516171819”
“2021222324252627282930313233343536373839”
“4041424344454647484950515253545556575859”
“6061626364656667686970717273747576777879”
“8081828384858687888990919293949596979899”;
const size_t length = digits10_v3(value);
uint32_t next = length - 1;
while (value 》= 100) {
const uint32_t i = (value % 100) * 2;
value /= 100;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
next -= 2;
}
// Handle last 1-2 digits
if (value 《 10) {
dst[next] = ‘0’ + uint32_t(value);
} else {
uint32_t i = uint32_t(value) * 2;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
}
return length;
}
int main() {
srand(100);
uint64_t digit10_array[ITEM_COUNT];
for( int i = 0; i 《 ITEM_COUNT; ++i )
{
digit10_array[i] = rand();
}
char buffer[BUFFERSIZE];
struct timeval start, end;
// digits10_v1
uint64_t sum1 = 0;
uint64_t time1 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i 《 RUN_TIMES; ++i )
{
sum1 += u64ToAscii_v1(digit10_array[i], buffer);
}
gettimeofday(&end,NULL);
time1 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v2
uint64_t sum2 = 0;
uint64_t time2 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i 《 RUN_TIMES; ++i )
{
sum2 += u64ToAscii_v2(digit10_array[i], buffer);
}
gettimeofday(&end,NULL);
time2 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v3
uint64_t sum3 = 0;
uint64_t time3 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i 《 RUN_TIMES; ++i )
{
sum3 += u64ToAscii_v3(digit10_array[i], buffer);
}
gettimeofday(&end,NULL);
time3 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
cout 《《 “sum1:” 《《 sum1 《《 “ sum2:” 《《 sum2 《《 “ sum3:” 《《 sum3 《《 endl;
cout 《《 “cost1:” 《《 time1 《《 “us cost2:” 《《 time2 《《 “us cost3:” 《《 time3 《《 “us”
《《 “ cost2/cost1:” 《《 (1.0*time2)/time1
《《 “ cost3/cost1:” 《《 (1.0*time3)/time1 《《 endl;
return 0;
}
/* 測試結果
g++ -g -O2 cplusplus_optimize.cpp -o cplusplus_optimize && 。/cplusplus_optimize
sum1:9944152 sum2:9944152 sum3:9944152
cost1:47305us cost2:42448us cost3:31657us cost2/cost1:0.897326 cost3/cost1:0.66921
*/
看到優化寫內存操作的威力了吧,讓我們再看一個減少寫操作的例子:
struct Bitfield {
int a:4;
int b:2;
int c:2;
};
Bitfield x;
int A, B, C;
x.a = A;
x.b = B;
x.c = C;
假定 A、B、C 都很小,且不會溢出,可以寫成
union Bitfield {
struct {
int a:4;
int b:2;
int c:2;
};
char abc;
};
Bitfield x;
int A, B, C;
x.abc = A | (B 《《 4) | (C 《《 6);
如果需要考慮溢出,也可以改為
x.abc = (A & 0x0F) | ((B & 3) 《《 4) | ((C & 3) 《《6 );
讀取效率
對于內存的寫,最好的辦法就是減少寫的次數,那么內存的讀取呢?教科書的答案是:盡可能順序訪問內存。理解這句話還是得從 cache line 開始,因為實際的 cpu 比較復雜,下面的表述嘗試做些簡化,如有問題,歡迎指正:
cache line
假設 L1cache 大小為 8K,cache line 64 字節、4way,那么整個 cache 會分成32 個集合, 81024/64=128=324,一個內存地址進入哪個 cache line 不是任意的,而是確定在某個集合中,可以通過公式 (set ) = (memory address) / ( line size) % (number of sets )來計算,如地址是 10000,則(set)=10000/64%32 = 28, 即編號為28的集合內的4個 cache line 之一。
用 16 進制來描述,10000=0x2710 ,一次內存讀取是 64bytes,那么訪問內存地址 10000 即意味著地址 0x2700~0x273F 都進集合編號為 28(0x1C) 的 cache line 中了。
cache miss
可以看出,順序的訪問內存是能夠比較高效而且不會因為 cache 沖突,導致藥頻繁讀取內存。那什么的情況會導致 cache miss 呢?
當某個集合內的 cache line 都有數據時,且該集合內有新的數據就會導致老數據的換出,進而訪問老數據就會出現 cache miss。
以先后讀取 0x2710, 0x2F00, 0x3700, 0x3F00, 0x4700 為例, 這幾個地址都在 28 這個編號的集合內,當去讀 0x4700 時,假定 CPU 都是以先進先出策略,那么 0x2710 就會被換出,這時候如果再訪問 0x2700~0x273F 的數據就 cache miss,需要重新訪問內存了。
可以看出變量是否有 cache 競爭,得看變量地址間的距離,distance = (number of sets ) (line size) = ( total cache size) / ( number of ways) , 即距離為3264 = 8K/4= 2K的內存訪問都可能產生競爭。
上面這些不光對變量、對象有用,對代碼 cache 也是如此。
建議
對于內存的訪問,可以考慮以下一些建議:
一起使用的函數存儲在一起。函數的存儲通常按照源碼中的順序來的,如果函數A,B,C是一起調用的,那盡量讓ABC的聲明也是這個順序
一起使用的變量存儲在一起。使用結構體、對象來定義變量,并通過局部變量方式來聲明,都是一些較好的選擇。例子見后文:
合理使用對齊(attribute((aligned(64)))、預取(prefecting data),讓一個cacheline能獲取到更多有效的數據
動態內存分配、STL容器、string都是一些常容易cache不友好的場景,核心代碼處盡量不用
int Func(int);
const int size = 1024;
int a[size], b[size], i;
。..
for (i = 0; i 《 size; i++) {
b[i] = Func(a[i]);
}
// pack a,b to Sab
int Func(int);
const int size = 1024;
struct Sab {int a; int b;};
Sab ab[size];
int i;
。..
for (i = 0; i 《 size; i++) {
ab[i].b = Func(ab[i].a);
}
靜態變量
讓我們再回到最前面的優化,u64ToAscii_v3 引入了局部靜態變量 (digits),是否合適?通常來說,要具體問題具體分析,沒有標準答案。
靜態變量和棧地址是分開的,可能會帶來 cache miss 的問題,通過去掉 static 修飾符,直接在棧上聲明變的方式可以避免,但這種做法可行有幾個前提條件:
變量大小是要限制的,不超出cache的大小(最好是L1 cache)
變量的初始化在棧上完成,故最好不要在循環內部定義,以避免不必要的初始化。
其實內存訪問和 CPU 運算是沒有一定的贏家,真正做優化時,需要結合具體的場景,仔細測量才能得到答案。
回顧
前面兩個實例分別從編譯器和內存使用的角度介紹了一些性能優化的方法,后面內容則會回到cpu,從指令并行的角度看看我們常見的邏輯控制有哪些可以優化的點。
從原理上來說,這個系列的優化不是特別區分語言,只是這里我們用C++來描述。
流水線
通常一個 CPU 可以并行執行多條指令,如:4 條浮點乘法,等待 4 個內存訪問、一個還為到來的分支比較,不同的運算單元也是可以并行計算,如 for(int i = 0; i 《 N; ++i) a[i]=0.2; 這里的 i 《 N 和 ++i 在 a[i]=0.2 可以同時執行。提升指令并行能力,往往就能達到提升性能的目的。
從流水線的角度看,指令 pipeline 的幾個階段:fetch、decode、execute、memory-access、write-back,除了存儲器的訪問效率會影響并行度外,下一條指令的 fetch/decode 也很關鍵,而跳轉和分支則是又一個攔路虎,這也是本文接下去要主要分析的地方。
函數本身開銷
函數調用使得處理器跳到另外一個代碼地址并回來,一般需要4 clock cycles,大多數情況處理器會把函數調用、返回和其他指令一起執行以節約時間。
函數參數存儲在棧上需要額外的時間( 包括棧幀的建立、saving and restoring registers、可能還有異常信息)。在64bit linux上,前6個整型參數(包括指針、引用)、前8個浮點參數會放到寄存器中;64bit windows上不管整型、浮點,會放置4個參數。
在內存中過于分散的代碼可能會導致較差的code cache
常見的優化手段
避免不必要的函數,特別在最底層的循環,應該盡量讓代碼在一個函數內。看起來與良好的編碼習慣沖突(一個函數最好不要超過80行),其實不然,跟這個系列其他優化一樣,我們應該知道何時去使用這些優化,而不是一上來就讓代碼不可讀。
嘗試使用inline函數,讓函數調用的地方直接用函數體替換。inline對編譯器來說是個建議,而且不是inline了性能就好,一般當函數比較小或者只有一個地方調用的時候,inline效果會比較好
在函數內部使用循環(e.g., change for(i=0;i《100;i++) DoSomething(); into DoSomething() { for(i=0;i《100;i++) { 。.. } } )
減少函數的間接調用,如偏向靜態鏈接而不是動態鏈接,盡量少用或者不用多繼承、虛擬繼承
優先使用迭代而不是遞歸
使用函數來替換define,從而避免多次求值。宏的其他缺點:不能overload和限制作用域(undef除外)
// Use macro as inline function
#define MAX(a,b) ((a) 》 (b) ? (a) : (b))
y = MAX(f(x), g(x));
// Replace macro by template
template 《typename T》
static inline T max(T const & a, T const & b) {
return a 》 b ? a : b;
}
分支預測應用場景
常見的分支預測場景有 if/else,for/while,switch,預測正確 0~2 clock cycles,錯誤恢復 12~25 clock cycles。
一般應用分支預測的正確率在90%以上,但個位數的誤判率對有較多分支的程序來說影響還是非常大的。分支預測的技術(或者說策略)非常多,這里不會展開介紹,對寫程序來說,我們知道越簡單的場景越容易預測正確:如分支都在在一個循環內或者幾乎沒有其他分支。
關鍵因素
如果對分支預測的概念和作用還不清楚的話,可以看看后面的參考文檔。幾個影響分支預測因素:
branch target buffer (BTB)
分支預測的結果存儲一個特殊的cache,該cache是個固定大小的hashtable,通過$pc可以計算出預測結果地址
在指令fetch階段訪問,使得分支目標地址在IF階段就可以讀取。預測不正確時更新預測結果
Return Address Stack (RAS)
固定大小,操作方式跟stack結構一樣,內容是函數返回值地址($pc+4), 使用BTB存儲
間接的跳轉不便于預測,如依賴寄存器、內存地址,好在絕大多數間接的跳轉都來自函數返回
函數返回地址預測使用BTB,如果關鍵部分的函數和分支較多,會引起BTB的競爭,進而影響分支命中率
常見的優化手段
1. 消除條件分支
代碼實例
if (a 《 b) {
r = c;
} else {
r = d;
}
優化版本1
int mask = (a-b) 》》 31;
r = (mask & c) | (~mask & d);
優化版本2
int mask = (a-b) 》》 31;
r = d + mask & (c-d);
優化版本3
// cmovg版本
r = (a 《 b) ?c : d;
bool 類型變換
實例代碼
bool a, b, c, d;
c = a && b;
d = a || b;
編譯器的行為是
bool a, b, c, d;
if (a != 0) {
if (b != 0) {
c = 1;
}
else {
goto CFALSE;
}
}
else {
CFALSE:
c = 0;
}
if (a == 0) {
if (b == 0) {
d = 0;
}
else {
goto DTRUE;
}
}
else {
DTRUE:
d = 1;
}
優化版本
char a = 0, b = 0, c, d;
c = a & b;
d = a | b;
實例代碼2
bool a, b;
b = !a;
// 優化成
char a = 0, b;
b = a ^ 1;
反例
a && b 何時不能轉換成 a & b,當 a 不可能為 false 的情況下
a | | b 何時不能轉換成 a | b,當 a 不可能為 true 的情況下
2. 循環展開
實例代碼
int i;
for (i = 0; i 《 20; i++) {
if (i % 2 == 0) {
FuncA(i);
}
else {
FuncB(i);
}
FuncC(i);
}
優化版本
int i;
for (i = 0; i 《 20; i += 2) {
FuncA(i);
FuncC(i);
FuncB(i+1);
Func
C(i+1); }
優化說明
優點:減少比較次數、某些CPU上重復次數越少預測越準、去掉了if判斷
缺點:需要更多的code cache or micro-op cache、有些處理器(core 2)對于小循環性能很好(小于65bytes code)、循環的次數和展開的個數不匹配
一般編譯器會自動展開循環,程序員不需要主動去做,除非有一些明顯優點,比如減少上面的if判斷3. 邊界檢查
實例代碼1
const int size = 16; int i;
float list[size];
。..
if (i 《 0 || i 》= size) {
cout 《《 “Error: Index out of range”;
}
else {
list[i] += 1.0f;
}
// 優化版本
if ((unsigned int)i 》= (unsigned int)size) {
cout 《《 “Error: Index out of range”;
}else {
list[i] += 1.0f;
}
實例代碼2
const int min = 100, max = 110; int i;
。..
if (i 》= min && i 《= max) { 。..
//優化版本
if ((unsigned int)(i - min) 《= (unsigned int)(max - min)) { 。..
4. 使用數組
實例代碼1
float a; int b;
a = (b == 0) ? 1.0f : 2.5f;
// 使用靜態數組
float a; int b;
static const float OneOrTwo5[2] = {1.0f, 2.5f};
a = OneOrTwo5[b & 1];
實例代碼2
// 數組的長度是2的冪
float list[16]; int i;
。..
list[i & 15] += 1.0f;
5. 整形的 bit array 語義,適用于 enum、const、define
enum Weekdays {
Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday
};
Weekdays Day;
if (Day == Tuesday || Day == Wednesday || Day == Friday) {
DoThisThreeTimesAWeek();
}
// 優化版本 using &
enum Weekdays {
Sunday = 1, Monday = 2, Tuesday = 4, Wednesday = 8,
Thursday = 0x10, Friday = 0x20, Saturday = 0x40
};
Weekdays Day;
if (Day & (Tuesday | Wednesday | Friday)) {
DoThisThreeTimesAWeek();
}
本塊小結
盡可能的減少跳轉和分支
優先使用迭代而不是遞歸
對于長的if.。.else,使用switch case,以減少后面條件的判斷,把最容易出現的條件放在最前面
為小函數使用inline,減少函數調用開銷
在函數內使用循環
在跳轉之間的代碼盡量減少數據依賴
嘗試展開循環
嘗試通過計算來消除分支
原文標題:干貨:C++的性能優化
文章出處:【微信公眾號:嵌入式ARM】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
C++
+關注
關注
22文章
2104瀏覽量
73498
原文標題:干貨:C++的性能優化
文章出處:【微信號:gh_c472c2199c88,微信公眾號:嵌入式微處理器】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
TMS320C28x優化C/C++編譯器v22.6.0.LTS





 如何優化C++語言的性能?
如何優化C++語言的性能?












評論