一、什么是微分算子符號?
描述線性系統的激勵函數和響應函數間關系的微分方程,具有以下形式:
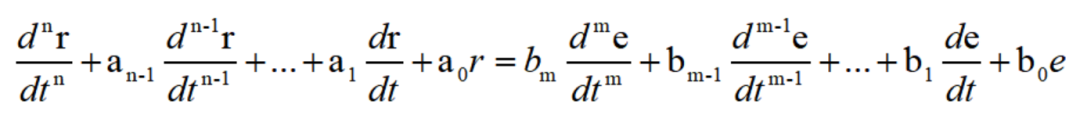
式中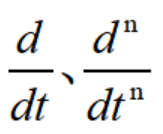 為時域中的微分算子符號,當它們作用于某一時間函數時,該函數就要對時間變量t分別進行一次和n此微分運算。現在為了方便計算,
為時域中的微分算子符號,當它們作用于某一時間函數時,該函數就要對時間變量t分別進行一次和n此微分運算。現在為了方便計算,
把微分算自符號用p來代表,即令:
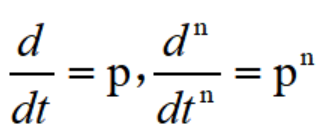
把積分算子用1/p來代表,即令:
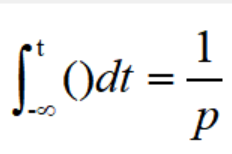
于是有:
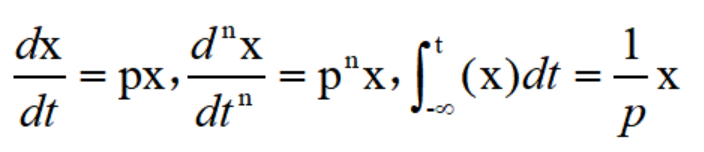
利用這樣的符號,積分微分方程或微分方程就可以用較為簡化的形式寫出。
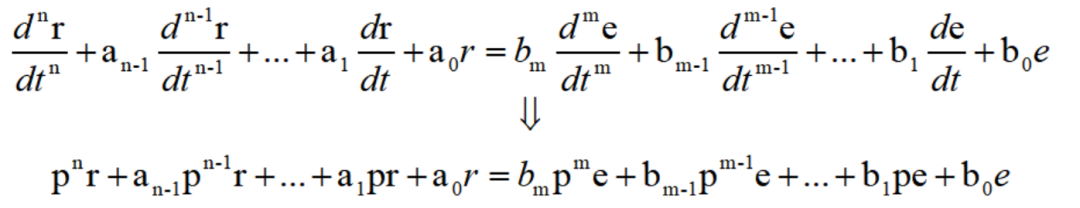
或者仿照代數方程把公共因子提出來的方法,還可以寫成:
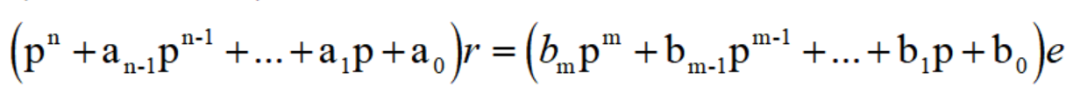
在這里,雖然把微分算子符號p像代數量那樣處理,但是不要忘記它不是代數量。因此,例如
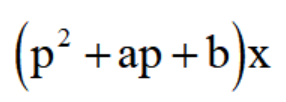
這樣的式子中,
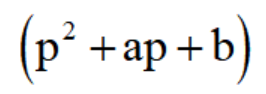
并不是用來與函數x相乘的代數量,而它作為一個整體,是一個作用在函數x的運算符號,代表著一定的運算過程,即
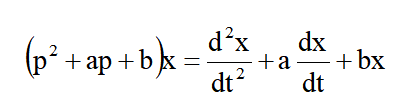
利用算子符號把微分方程寫成代數方程的算子方程,于是就會自然地闡述這樣的一個問題,即代數方程中的運算規則在算子方程中是否適用?
對于這個問題的回答是:一般適用,但有例外。
例如,在代數方程中有關系
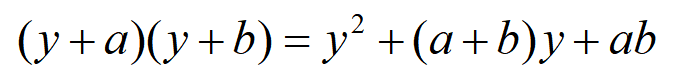
在算子方程中關系
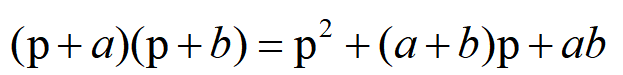
是否也成立呢?只要加以運算檢驗,就可以證明這關系是成立的。證明如下
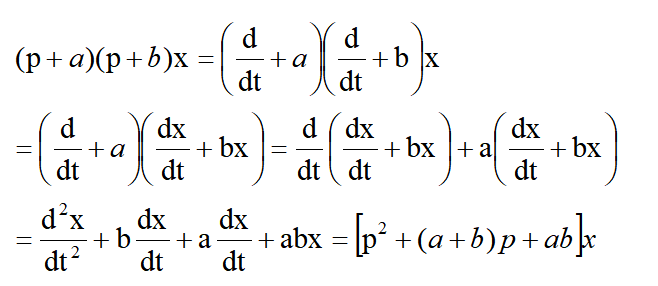
把這檢驗法加以推廣,不難得出結論,即由p的多項式所組成運算符號可以像代數式那樣進行相乘和那樣因子分解。
再例如:
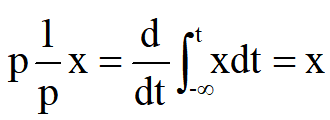
這里也像代數式中一樣,分子分母中的p可以消去。但是
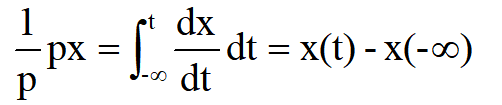
這里分母和分子中的p一般就不能消去。這表明
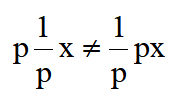
也就是說,微分和積分的運算次序不能任意顛倒,兩種運算也不一定能抵消。同樣,若將式
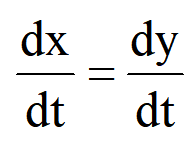
兩邊積分,可得:x=y+c
其中c為積分常數。由此可見,在等式px=py,雙方的算子p一般也不好消去。
以上說明,代數量的運算規則對于算子符號一般也可以應用,只是在分子分母中或等式兩邊中相同的算子符號卻不能隨便消去。
二、微分方程的算子形式和拉普拉斯變換式之間的是什么關系?
描述系統的輸入輸出的微分方程一般形式有:
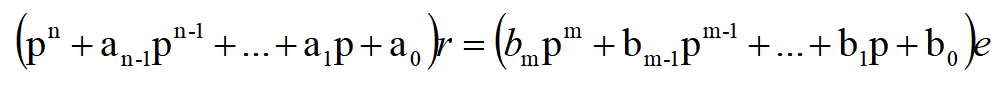
把左右兩邊p的多項式分別記為D(p)和N(P),則有
D(p)r(t)=N(P)e(t)
這一微分方程又可進一步寫成
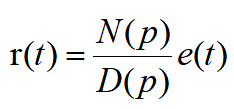
把p的分式N(p)/D(p)定義為轉移算子H(p),即H(p)=N(p)/D(p)
于是,在時域中響應函數與激勵函數之間的關系,就可用以下簡明的一般形式表示:r(t)=H(p)e(t)
當求系統的零輸入響應時,激勵函數e(t)為零,就要解齊次方程
D(p)r(t)=0
當求系統的零狀態響應時,則要解非齊次方程
r(t)=H(p)e(t)
把微分方程的時域算子的形式與拉普拉斯的變換式相比較,將下式進行拉普拉斯變換,得
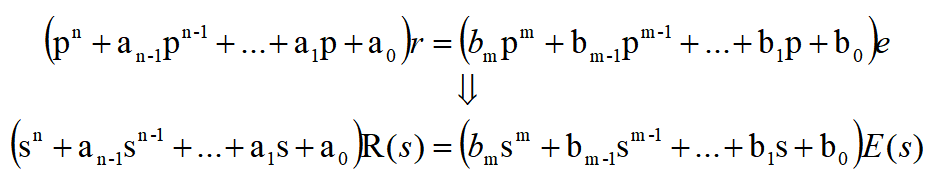
把此等式左邊s得多項式記為D(s),右邊s得多項式記為N(s),則有
D(s)R(s)=N(s)E(s)
或者R(s)=N(s)E(s)/D(s)=H(s)E(s)
其中H(s)=N(s)/D(s)為在復頻域中表示響應函數和激勵函數之間關系的轉移函數。
當求系統的零輸入響應時,激勵函數E(s)為零,D(s)R(s)=N(s)E(s)成為D(s)R(s)=0。系統的零輸入響應由特征方程D(s)=0的根決定。
當求系統的零狀態響應時,只要將式R(s)=N(s)E(s)/D(s)=H(s)E(s)進行拉普拉斯反變換即得。
把拉普拉斯的式子與算子形式的微分方程式相比較,就可以發現各對應得關系式之間,具有完全相似得形式。

可以看到,
在拉普拉斯變換式中,R(s)、E(s)、H(s)等都是復頻率變量s的函數,H(s)E(s)即表示這兩個函數相乘。
而在算子形式的微分方程中,r(t)、e(t)都是時間函數,H(p)是時域中的運算符號,H(p)e(t)并不表示兩個函數相乘,而只表示對方程中的時間函數進行某種特定的運算。
算子形式的微分方程和其拉普拉斯變換式之間的相似性,很自然會引起人們提出這樣的問題,即在求解系統的響應時,是否也具備同樣的相似性?
或者說,能不能把拉普拉斯變換中的一套求解法搬過來用于時域中求解微分方程呢?
對于求系統的零輸入響應,回答是肯定的。
但是對于求系統的零狀態響應,除了兩者均以疊加原理為共同基礎外,在激勵函數的分解和系統單元激勵函數的響應等具體形式上,時域分析法就不同于復頻率分析法,然而兩種分析法之間,又存在著密切的關系。
編輯:jq
-
函數
+關注
關注
3文章
4306瀏覽量
62430 -
微分方程
+關注
關注
0文章
21瀏覽量
9507
原文標題:什么是微分算子符號?微分方程的算子形式和拉普拉斯變換式之間的是什么關系?
文章出處:【微信號:monizj,微信公眾號:模擬札記】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
先進產能設備提供商拉普拉斯科創板上市
拉普拉斯變換的作用及意義
數字信號處理三大變換關系包括什么
降本增效取得新進展,拉普拉斯申請晶圓圖形化工藝專利
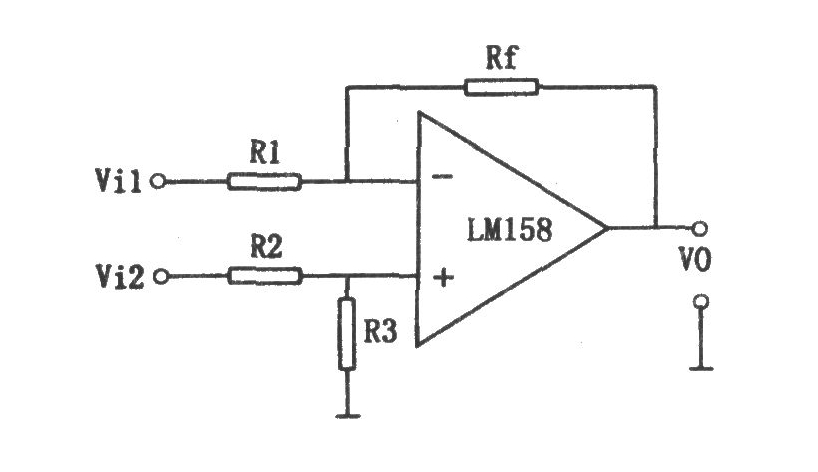
運放減法電路微分方程怎么求
Intersolar 2024丨慕尼黑,拉普拉斯來了!
拉普拉斯IPO:科技與產業深度融合,實現業務領域延展
證監會同意拉普拉斯上交所科創板IPO注冊
拉普拉斯科創板IPO過會
傅里葉變換和拉普拉斯變換的關系是什么
賽普拉斯的NV-SRAM接口解決方案




 微分方程的算子形式和拉普拉斯變換式之間的是什么關系?
微分方程的算子形式和拉普拉斯變換式之間的是什么關系?










評論