你能想象某一天打開深度學習的詞條，發(fā)現：

深度學習的江湖已經能夠被統一了嗎？

幾何學上的對稱性可以玩轉整個深度學習嗎？

通過對稱性和的變換，可以提煉出覆蓋CNNs, GNNs, LSTMs, Transformers, DeepSets, mesh CNN等一切你所需構建的架構嗎？

不要驚訝，不要懷疑。

一百多年前埃爾蘭根大學一位23歲的小伙就給出了答案。

他僅憑一己之力開創(chuàng)的“埃爾蘭根計劃”，從而在幾何學上做出了一項開創(chuàng)性的工作，改變了數學史。

幾何學對稱問題的源起

在1872年10月，德國的埃爾蘭根大學任命了一位新的年輕教授。按照慣例，他被要求提供一個就職研究計劃，他以長而乏味的標題Vergleichende Betrachtungen über neuere geometrische Forschungen（“對幾何學最新研究的比較評論”）進行了發(fā)表。

這位就是菲利克斯·克萊因（Felix Klein），當時他只有23歲，他的開創(chuàng)性工作被稱為“埃爾蘭根計劃”，在數學史上有濃墨重彩的一筆。

十九世紀簡直就是幾何學的大爆發(fā)時代。歐幾里得之后的近兩千年來，龐塞萊特（Poncelet）構造了投影幾何，高斯（Gauss）、波利亞伊（Galys）和洛巴切夫斯基（Lobachevsky）構造了雙曲線幾何，而黎曼（Riemann）構造了橢圓幾何。

克萊因的Erlangen program（埃爾蘭根綱領）的突破性體現在研究幾何學時運用了結構的對稱性。克萊因采用群論的形式來定義此類轉換，并采用群及其子群的層次結構來分類由此產生的不同幾何形狀。

因此，剛性運動會產生傳統的歐幾里得幾何，而仿射或投影變換分別產生仿射和投影幾何。

Erlangen program不僅對幾何和數學影響非常深遠，同時也影響了物理領域，對稱性可以從第一原理推導守恒律，即Noether定理。

經過幾十年的發(fā)展，直到楊振寧和米爾斯在1954年提出的規(guī)范不變性的概念的廣義形式證明了這一基本原理，成功地統一了除重力以外的所有自然基本力。

這種標準模型已經描述了我們目前所知道的所有物理學知識。

所以啊，還是諾貝爾獎得主物理學家菲利普·安德森（Philip Anderson）的話說得好：

“it is only slightly overstating the case to say that physics is the study of symmetry.”

“說物理學本質上就是研究對稱性的，這只是有點夸大其詞了。”

目前深度學習領的現狀和19世紀的幾何情況驚人的類似：

一方面，在過去的十年中，深度學習帶來了數據科學的一場革命，并完成了許多以前被認為無法實現的任務：無論是計算機視覺，語音識別，自然語言翻譯，還是下圍棋。

另一方面，現在存在一個針對不同類型數據的不同神經網絡體系結構的“動物園”，但統一的原理很少。這樣很難理解不同方法之間的關系，也導致相同概念的多次發(fā)明和資源的浪費。

在機器學習中，對稱性的重要性實際上早已得到認可。

尤其是在模式識別和計算機視覺的應用中，有關等變特征檢測的早期工作可以追溯到Shunichi Amari和Reiner Lenz。

在神經網絡文獻中，Marvin Minsky和Seymour Papert提出的感知器的群不變性定理對（單層）感知器學習不變性的能力提出了基本限制。

幾何深度學習

具體怎么個“統一”，請看采用的“幾何深度學習”：

幾何深度學習是Michael M. Bronstein，Joan Bruna，Taco Cohen，Petar Veli?kovi? 等人中引入的一個籠統術語，指的是類似于Klein的Erlangen program，在幾何機器學習上統一的嘗試的總稱。

它有兩個目的：首先，提供一個通用的數學框架以推導最成功的神經網絡體系結構；其次，給出一個建設性的過程，并以有原則的方式構建未來的體系結構。

在最簡單的情況下，有監(jiān)督的機器學習本質上是一個函數估計問題：給定訓練集上某些未知函數的輸出（例如標記的狗和貓圖像），人們試圖從某個假設函數類別中找到一個適合訓練的函數f ，并可以預測以前看不見的輸入的輸出。

在過去的十年中，大型的、高質量的數據集（如ImageNet）的可用性與不斷增長的計算資源（GPU）吻合，從而可以設計功能豐富的類，這些類可以內插此類大型數據集。

神經網絡似乎是表征功能的合適選擇，因為即使是最簡單的體系結構（如Perceptron），僅使用兩層時也可以生成密集類的功能，從而可以將任何連續(xù)函數近似為任何所需的精度，這種特性稱為“通用逼近”（Universal Approximation）。

低維問題的設置是逼近理論中的經典問題，該問題已得到廣泛研究，并通過精確的數學方法控制估算誤差。但是，在高維度上情況卻完全不同：人們可以很快地看到，即使近似一類簡單的Lipschitz連續(xù)函數，樣本數量也隨維度呈指數增長，這種現象俗稱“維數詛咒”。

由于現代機器學習方法需要處理成千上萬甚至數百萬個維度的數據，因此維度的詛咒總是在幕后出現，使得我們無法通過樸素的方式進行學習。

△維度詛咒的圖示：為了近似由高斯核構成的Lipschitz連續(xù)函數，該函數位于誤差為ε的d維單位超立方體（藍色）的象限中，需要

在計算機視覺問題（例如圖像分類）中可能最好地看到了這一點。即使是很小的圖像也往往具有很高的尺寸，但是從直觀上講，當人們將圖像解析為向量以將其饋反饋送到感知器時，很多圖像的結構會被破壞并丟棄。如果現在僅將圖像移位一個像素，則向量化的輸入將有很大的不同，并且神經網絡將需要顯示很多示例，因此必須以相同的方式對移位的輸入進行分類。

原理簡介

通過對稱性，不變性和群的視角，包含兩大原理：

“先驗對稱性”

在許多高維ML問題的情況下，我們可以采用一個附加結構信息，它來自輸入信號的幾何形狀。我們稱這種結構為“先驗對稱性”，它是一種普遍有效的原理，它使我們對由維數引起的問題感到樂觀。在我們的圖像分類示例中，輸入圖像x不僅是d維向量，而且是在某個域Ω上定義的信號，在這種情況下，該信號是二維網格。

域的結構由對稱群變換????（在我們的示例中為一組二位變換-作用于域上的點。在信號????（Ω）的空間中，底層域上的群動作（群元素，????∈????）通過所謂的群表征ρ（????）來表示，在我們的例子中，上述操作是平移操作，即一個作用于d維向量的d×d矩陣。

輸入信號底層的域的幾何結構為我們試圖學習的函數 f 的類別施加了架構信息。一個不變函數可以不受群的操作作用的影響，即對于任何????∈????和x，f（ρ（????）x）= f（x）。另一方面，函數可能具有相同的輸入和輸出結構，并且以與輸入相同的方式進行轉換，這種函數稱為等變函數，即滿足f（ρ（????）x）= ρ（???? ）f（x）。

在計算機視覺領域中，圖像分類是一種典型的人們希望得到不變函數的任務（例如，無論貓位于圖像的什么位置，我們都希望將該圖分類為貓）；而圖像分割任務的輸出是一個像素級別的標簽掩模，這是一種等變函數（分割掩模需要遵循輸入圖像的變化）。

“尺度分離”

另一個強大的幾何先驗是“尺度分離”。在某些情況下，我們可以通過“同化”附近的點并產生與粗粒度算子P相關的信號空間的層次結構，來構建域的多尺度層次結構（下圖中的Ω和Ω’）。

在這些粗尺度上，我們可以應用粗尺度函數。我們分析出，如果一個函數 f 可以被近似為粗粒度算子 P 和粗尺度函數的組合 f≈f’°P，則 f 是局部穩(wěn)定的。盡管 f 可能取決于長距離依賴，如果 f 是局部穩(wěn)定的，它們可以被分解為局部交互，然后向著粗尺度傳播。

這兩個原理為他們提供了一個非常通用的深度學習藍圖，可以在大多數用于表示學習的流行深度神經體系結構中得到認可：一個典型設計由一系列等變層（例如，CNN中的卷積層）組成，可能遵循通過不變的全局池層將所有內容聚合到一個輸出中。在某些情況下，也可以通過一些采用局部池化形式的粗化過程（coarsening procedure）來創(chuàng)建域的層次結構。

這是一種非常通用的設計，可以應用于不同類型的幾何結構，包括幾何深度學習的“ 5G”（Grid,Groups,Graphs,Geodesics & Gauges）：網格（具有全局轉換群的齊次空間），圖形（以及特殊情況下的集合）和流形，幾何先驗通過全局等距不變性表示（可以使用測地學表示） 和局部規(guī)范的對稱性。

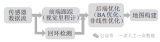
這些原則的實現導致了深度學習中當今存在的一些最流行的體系結構：從平移對稱導出的卷積網絡（CNN）、圖神經網絡、DeepSets和Transformers，實現了置換不變性， 時間扭曲不變導出的門控RNN（例如LSTM網絡），以及由規(guī)范對稱性導出的計算機圖形和視覺中使用的 Intrinsic Mesh CNN。

下一步他們還打算在“ 5G”上繼續(xù)“幾何深度學習”藍圖。

貌似高深的理論，用到了群論、微分幾何和各類機器學習高級算法，期待有更多研究人員參與并開展進一步深入研究。

未來，也許整個深度學習“動物園”的在原理上的統一真的不是夢。

責任編輯：haq