之前提出了兩種標(biāo)準(zhǔn)方法來為一階RC低通濾波器制定s域傳遞函數(shù)。簡(jiǎn)要回顧一些基本概念:傳遞函數(shù)在數(shù)學(xué)上表示濾波器的頻域輸入到輸出行為;可以用變量s來表示傳遞函數(shù),它代表復(fù)雜的頻率,當(dāng)需要計(jì)算特定頻率的幅度和相位響應(yīng)時(shí)可以用jω代替s ;傳遞函數(shù)的標(biāo)準(zhǔn)化形式就像一個(gè)模板,可以幫助我們快速確定濾波器的定義特征;對(duì)標(biāo)準(zhǔn)化一階傳遞函數(shù)的數(shù)學(xué)處理使我們能夠證明濾波器的截止頻率是幅度減小3dB并且相位偏移-45°的頻率。
極點(diǎn)和零點(diǎn)
假設(shè)我們有一個(gè)傳遞函數(shù),其中變量s出現(xiàn)在分子和分母中。在這種情況下,至少一個(gè)s值將使分子為零,并且至少一個(gè)s值將使分母為零。使分子為零的值是傳遞函數(shù)零點(diǎn),并且使分母為零的值是傳遞函數(shù)極點(diǎn)。讓我們考慮以下示例:
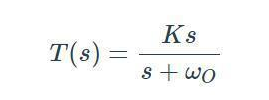
在這個(gè)系統(tǒng)中,在s=0時(shí)為零點(diǎn),在s=–ωo時(shí)為極點(diǎn)。極點(diǎn)和零點(diǎn)定義了濾波器的特征。如果你知道極點(diǎn)和零點(diǎn)的位置,則可以獲得有關(guān)系統(tǒng)如何響應(yīng)不同輸入頻率的信號(hào)的信息。
極點(diǎn)和零點(diǎn)的影響
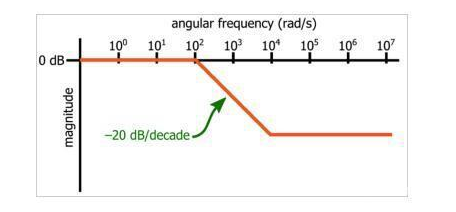
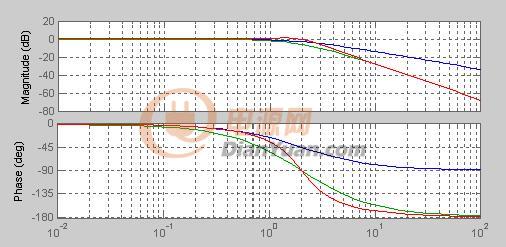
波特圖提供了極點(diǎn)或零點(diǎn)與系統(tǒng)輸入與輸出行為之間關(guān)系的直觀可視化。極點(diǎn)頻率對(duì)應(yīng)于角頻率,在該角頻率處,振幅曲線的斜率減小20dB /decade,并且一個(gè)零點(diǎn)對(duì)應(yīng)于一個(gè)角斜率,在該頻率下,斜率增加20dB /decade。在下面的示例中,波特圖是系統(tǒng)的振幅響應(yīng)的近似值,該系統(tǒng)的極點(diǎn)為10 2弧度/秒(rad / s),零點(diǎn)為10 4 rad / s。
相位效應(yīng)
在上一篇文章中,我們看到低通濾波器的相位響應(yīng)的數(shù)學(xué)原點(diǎn)是反正切函數(shù)。如果我們使用反正切函數(shù)(更具體地是負(fù)反正切函數(shù))來生成相位(以度為單位)與對(duì)數(shù)頻率的關(guān)系圖,最終得到以下曲線:
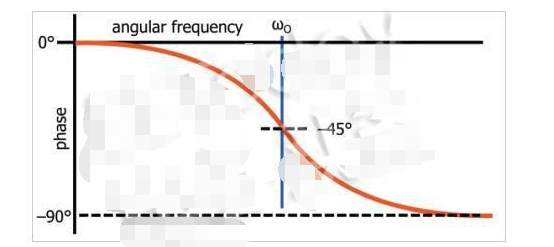
由極點(diǎn)產(chǎn)生的相移的波特圖近似是表示相移的-90°的直線。該線以極點(diǎn)頻率為中心,并且每十倍頻率下具有-45度的斜率,這意味著向下傾斜的線在極點(diǎn)頻率之前十倍頻率開始并且在極點(diǎn)頻率之后十倍頻率結(jié)束。除了線具有正斜率之外,零點(diǎn)影響是相同的,使得總相移是+ 90°。以下示例表示一個(gè)系統(tǒng),其極點(diǎn)為10 2 rad / s,零點(diǎn)為10 5 rad / s。
隱藏的零點(diǎn)
低通濾波器的傳遞函數(shù)可以寫成如下:
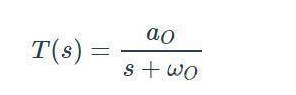
這個(gè)系統(tǒng)有零點(diǎn)嗎?如果我們應(yīng)用本文前面給出的定義,將得出結(jié)論,它不是變量s不出現(xiàn)在分子中,因此s的任何值都不會(huì)導(dǎo)致分子等于零。事實(shí)證明,它確實(shí)有一個(gè)零點(diǎn),為了理解原因,我們需要考慮傳遞函數(shù)極點(diǎn)和零點(diǎn)更一般化的定義:零點(diǎn)(z)發(fā)生在s的值上,它導(dǎo)致傳遞函數(shù)減小到零,極點(diǎn)(p)發(fā)生在s的值上,導(dǎo)致傳遞函數(shù)趨向于無窮大:
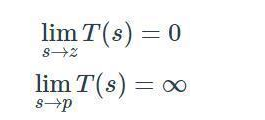
一階低通濾波器的s值是否會(huì)導(dǎo)致T(s)→0?是的,即s =∞。因此,一階低通系統(tǒng)在ωo處有極點(diǎn),在ω=∞處有零點(diǎn)。嘗試在ω=∞處提供零點(diǎn)的物理解釋:它表示濾波器不能繼續(xù)“永久”衰減(其中“永久”指的是頻率,而不是時(shí)間)。如果設(shè)法創(chuàng)建一個(gè)輸入信號(hào),其頻率繼續(xù)增加直到達(dá)到無窮大rad / s,則s =∞時(shí)的零點(diǎn)會(huì)使濾波器停止衰減,即振幅響應(yīng)的斜率從-20 dB /decade到0 dB /decade。
總結(jié)
我們已經(jīng)探索了傳遞函數(shù)極點(diǎn)和零點(diǎn)的基本理論和實(shí)踐方面,并且我們已經(jīng)看到在濾波器的極點(diǎn)和零點(diǎn)頻率及其振幅和相位響應(yīng)之間建立直接關(guān)系。
責(zé)任編輯人:CC
-
傳遞函數(shù)
+關(guān)注
關(guān)注
0文章
101瀏覽量
13871 -
零點(diǎn)
+關(guān)注
關(guān)注
0文章
17瀏覽量
10808
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
基于傳遞函數(shù)的頻率補(bǔ)償辦法
傳遞函數(shù)
關(guān)于dcdc的零點(diǎn)和極點(diǎn)的理解是什么
基于對(duì)數(shù)誤差準(zhǔn)則的HRTF共極點(diǎn)零點(diǎn)建模方法
傳遞函數(shù)中零點(diǎn)的解決方案
電路中極點(diǎn)與零點(diǎn)的產(chǎn)生與影響
晶體濾波器四極點(diǎn)是什么_晶體濾波器四極點(diǎn)怎么調(diào)
詳解傳遞函數(shù)的零點(diǎn)和極點(diǎn)
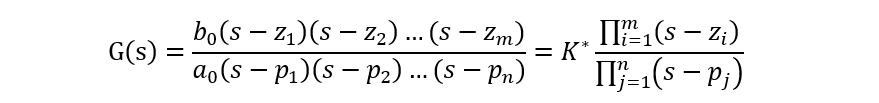
傳遞函數(shù)中的極點(diǎn)和零點(diǎn)有何影響?
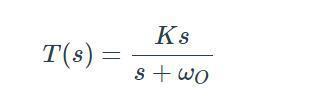




 傳遞函數(shù)極點(diǎn)和零點(diǎn)的影響是什么
傳遞函數(shù)極點(diǎn)和零點(diǎn)的影響是什么










評(píng)論