本來這期應該講Buck的尖峰的，不過遇到些問題，所以就往后拖一拖吧，這次來個簡單點兒的。

來看看傳遞函數，也就是我們經常看到的H（s）。

傳遞函數是怎么定義的呢？

百科是這么定義的：

【傳遞函數是指零初始條件下線性系統響應（即輸出）量的拉普拉斯變換（或z變換）與激勵（即輸入）量的拉普拉斯變換之比。記作G（s）=Y（s）/U（s），其中Y（s）、U（s）分別為輸出量和輸入量的拉普拉斯變換】

通俗理解就是，在電路應用中，如果我們把一個電路看作黑匣子，它有輸入端，有輸出端，傳遞函數就是輸出與輸入的比值。

只不過這個比值通常是頻率的函數，同時還包含相位信息。s=jw，w就是頻率，j包含了相位信息。

傳遞函數常會在分析環路穩定性，以及濾波器設計中用到，列出了傳遞函數，剩下的內容其實就是數學的分析了，也就是計算機干的事兒了。

我以前講過LC濾波器的，使用Matlab畫過增益Av曲線，其實也就是傳遞函數。只不過當時沒指出來，道理是一樣的。

如何寫出傳遞函數？

這是一個簡單的電路，它的傳遞函數是怎么樣的呢？

很簡單，運用歐姆定律。如果電路中只有電阻，我們應該都會使用歐姆定律求得輸出的電壓值。

但是這個電路中還有電感和電容，怎么辦呢？

其實我們也可以通過歐姆定律來求得電壓值，電感的阻抗是jwL，電容的阻抗是1/jwC，電阻的阻抗是R。輸出為電容C上面獲得的分壓，所以輸出與輸入的比值為：

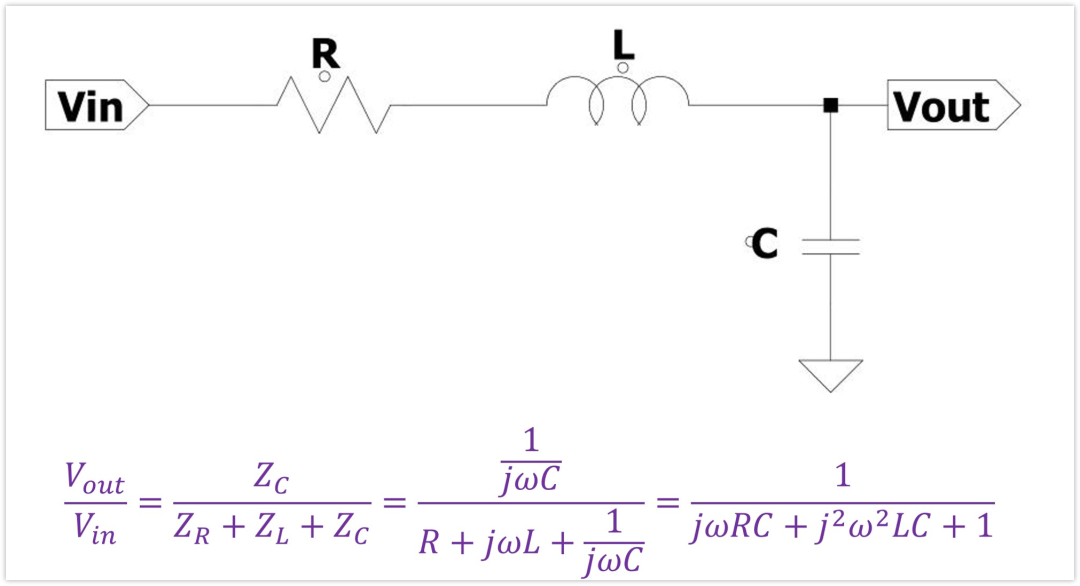
現在我們只需要將自變量改改，令s=jw，傳遞函數H（s）就出來了。

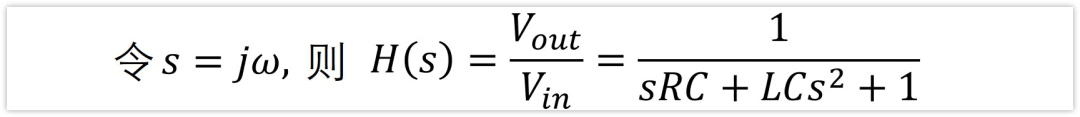
為啥要令s=jw呢？其實這一步就是將傅里葉變換變成了拉普拉斯變換。

啥？我沒看到傅里葉變換啊？我感覺我多嘴了。。。

更簡單的方式：

我們直接令s=jw，那么電感的阻抗是sL，電容的阻抗1/sC。這樣傳遞函數就能更快出來：

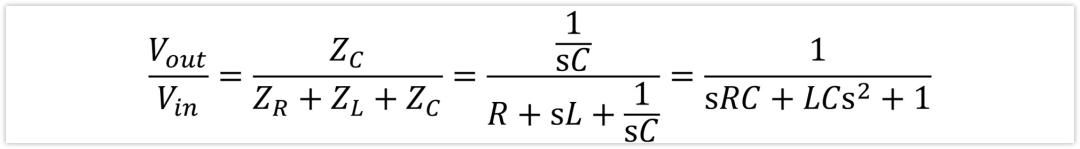
有了傳遞函數，借助計算機，代入公式，可以很輕松得到幅頻曲線和相位曲線。

下圖是R=1K，L=1uH，C=1uF時的曲線：

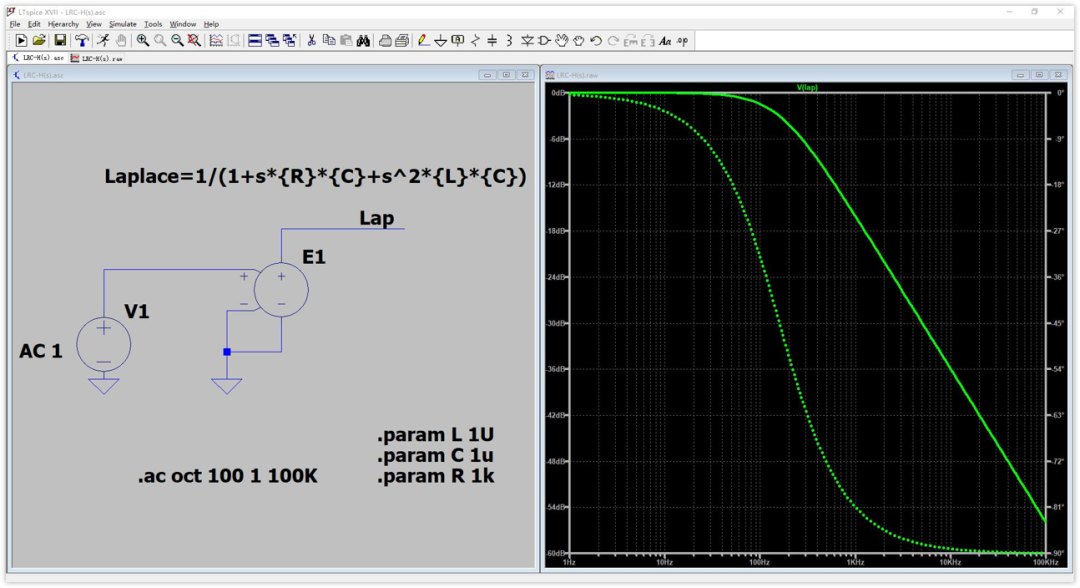
相信現在你應該知道了傳遞函數到底用來干什么的了吧。

編輯：jq