復頻率現在已是一個廣泛熟悉而通用的名詞,所以這里仍舊用它。復頻率可以方便地表示在一個復平面上,如下圖所示。
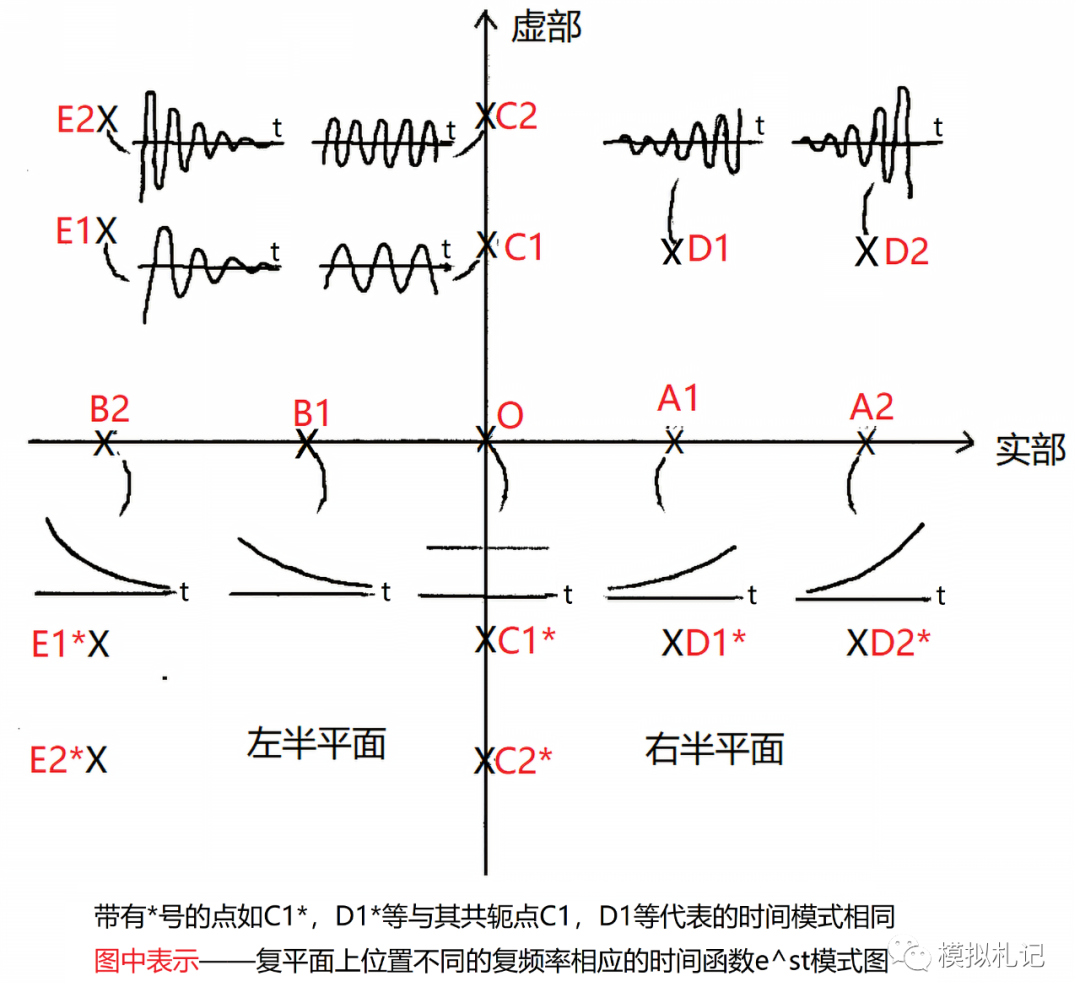
水平軸為實軸(σ軸),垂直軸為虛軸(jω),則不同的s值應于復平面上不同位置的點。
因為s的虛部ω反應指數函數的頻率,而實部σ則反映指數函數的幅度變化率。因此在復平面實軸上的點如A1、A2、B1、B2等。由于ω=0,所代表的是隨時間按指數規律單調增長或衰減的指數信號。
在σ正方向上σ>0,代表的是隨時間增長的指數信號。在σ軸負方向上σ<0,代表的是隨時間衰減的指數信號。且如點的位置距離虛軸愈遠,則σ的絕對值愈大,即意味著信號的增長或衰減速率愈大。
(1)試比較點A1與A2及B1與B2。A1、A2在正實軸上,代表的是隨時間增長的指數信號,而B1、B2在負實軸上,代表的是隨時間衰減的信號。
A1、B1比A2、B2距虛軸較近,所以A1、B1代表的指數信號隨時間的變化較A2、B2所代表的信號隨時間的變化較慢。
(2)在坐標原點O所代表的信號則是不隨時間變化的直流信號。
(3)在虛軸上的點則因為б=0,所以代表的是等幅的正弦振蕩信號,且頻率隨點距實軸的距離增加而增加。

(4)對于既不是實軸又不是虛軸上點,因為s為復數,所代表的是幅度按指數規律變化的“正弦振蕩”信號。在做半平面是幅度按指數規律衰減的正弦信號,在右半平面是幅度按指數規律增長的正弦信號。

當然,如果點距離虛軸愈遠,則幅度的變化速率愈快,如距實軸愈遠,則信號的頻率愈高。

通過上面的分析可以看出復平面上的每一點都對應于指數函數的一個確定的模式。需要指出的是在這里也會出現負頻率的信號,如C1*、D1*等。
其原因和傅里葉變換一樣,是由于用指數分量來表示信號的結果。
正如傅里葉變換中所指數的一個正頻率(s=jω)的指數函數與一個負頻率(s=-jω)的指數函數可以合并成一個等幅正弦信號:
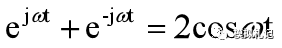
同樣兩個復頻率為共軛對(s=σ+jω,及s=σ-jω)的指數函數也可以合并成一個幅度按指數規律變化的正弦信號:
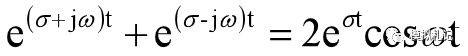
因此任一函數被分解為指數函數之和的時候,其復頻率一定是共軛成對出現的,不存在只有一個單獨的負頻率的情況。
通過上面對復頻率的說明,可以更清楚的看到,雙邊或單邊拉普拉斯變換都是把函數分解為無窮多個具有復頻率s的指數函數之和。
而傅里葉變換只是雙邊拉普拉斯變換中s=jω的一種特殊情況,即分解沿著復平面的虛軸進行的。
文章出處:【微信公眾號:模擬札記】
責任編輯:gt
-
頻率
+關注
關注
4文章
1446瀏覽量
59153 -
函數
+關注
關注
3文章
4306瀏覽量
62430
原文標題:復域與時域,復頻率與時間函數的關系
文章出處:【微信號:monizj,微信公眾號:模擬札記】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 復頻率與時間函數兩者之間的關系解析
復頻率與時間函數兩者之間的關系解析











評論