PID是十分優美的控制算法,在工業控制應用地十分廣泛,有的時候,無需知道系統模型的情況下,只要經驗法去調整參數P、參數I和、參數D就可以到達期望的控制效果;
不過之前一直停留在把系統當作黑盒的方式進行調試,根據系統的時間響應判斷是否達到期望的效果;
以前參與無人機研發的時候,我們遇到一個問題,外部的擾動會把飛控激勵起來造成機身的振動;
要解決掉的話,如果調飛控,又會對云臺造成影響,最終航拍效果不太好;
我們嘗試了很多工程方法,花了大量時間,都無法解決;這個項目看樣子是要黃了;
后來飛控負責人和云臺負責人激烈討論,在白板上畫伯德圖,講起相位裕度,幅值裕度;你的系統挪一下頻譜,給我留出更多的余量;退一步海闊天空;
很神奇,后來問題就順利解決了,項目順利上線;
所以我感覺有必要對部分的知識點進行復習和簡單的掃盲,因為嘗試從數學角度對系統性能進行分析,會涉及到,系統建模,零極點,穩定性,基本差不多還給老師了,所以這里不會太深入。
線性時不變系統
通常來說,對于上述的零點和極點的分析,前提是系統需要是LTI系統(linear time-invariant system);這里簡單介紹一下,對于這種系統有兩點:1 線性;2 時不變;
線性
對于系統,任意輸入X,最終系統輸出得到Y;
那么如果輸入為K*X,那么最終輸出為K*Y;
例如:
系統增益為100;
即輸入5可以得到輸出5*100;
那么輸入5*K,可以得到輸出5*K*100;
疊加性
如果系統輸入X可以得到輸出結果f(X),如果X=a+b;
那么必須存在 f(X) = f(a) + f(b);
時不變
系統中,輸入信號X,則得到輸出信號Y,那么一個經過了延遲T的輸入信號X,得到的輸出信號也只是一個被延遲T的Y,而不會是其他值;
也就是說X(t-T)的輸出就是Y(t-T);
什么是零點和極點?
在數字信號處理或者控制理論中,對于輸入量和輸出量,可以表示為:
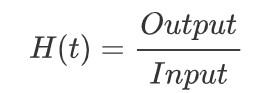
如果對于進行拉普拉斯變換,那么可以得到:
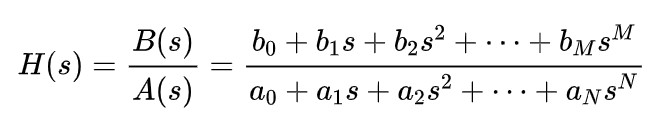
對于連續系統,需要進行拉普拉斯變換變換,則從時域變換到頻域;
對于離散系統,則需要進行z變換;
輸入,輸出以及傳遞函數的關系如下所示;
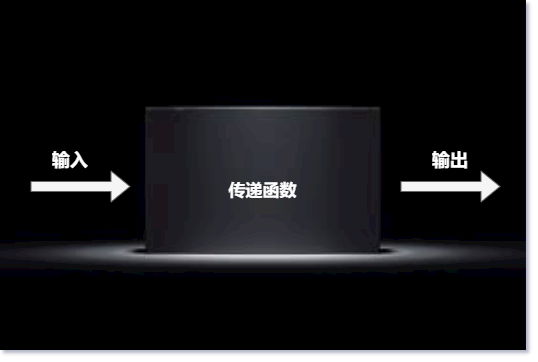
傳遞函數
零點
上述公式中,存在使得的解,即分母的解;
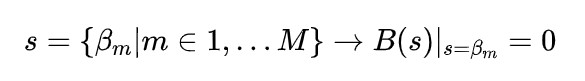
極點
上述公式中,存在使得的解,即分子的解;
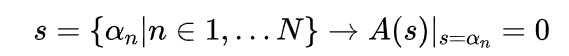
舉例
假設存在傳遞函數;
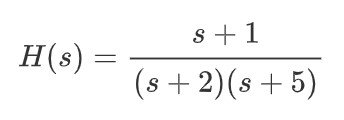
則零點為 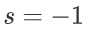 ;
;
極點為 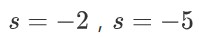 ;
;
系統的穩定的條件
從時域角度來講:
系統的穩定與否卻決于,當,系統輸出最終收斂,則認為系統是穩定的;具體如如下所示;
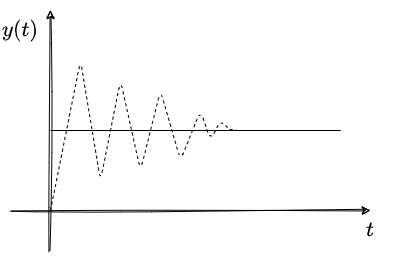
收斂
或者結論可以是這樣子的;
穩定性判斷:在零初始條件下,當且僅當,閉環系統的單位沖激響應為零時,系統是穩定的。
這里又引入了單位沖激響應;什么是沖激響應?
顧名思義,沖激響應,一定是一個函數,可以想象一下,感覺形狀和火柴及其相似;
這畫面感很強,具體如下所示;
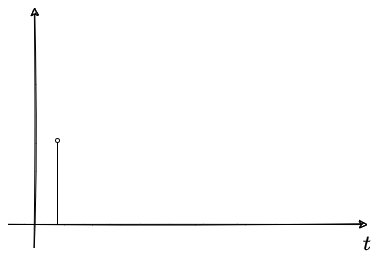
單位沖激響應
所以在這里我們將上面的進行時間T進行離散化,具體如下圖所示;
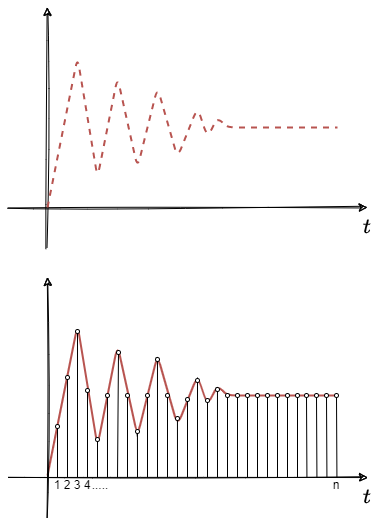
所以這里我們可以發現,可以通過單位沖激響應進行幅值變化和相位移動來表示;
實際上,我們根本只需要讓這些信號都輸入系統,前面講到過線性時不變;
所以我們只需要讓這些信號(1,2,3....n)中的任意一個信號進行歸一化(單位沖激響應);
對齊到t=0時刻,再對輸出乘以不同系數,延遲不同時間,就得到了所有的輸出.
好像有點扯遠了;
所以結論成立:在零初始條件下,當且僅當,閉環系統的單位沖激響應為零時,系統是穩定的;
從頻域角度來講:
對于高階系統無法求時域響應的時候,這時候就需要從閉環傳遞函數的零極點進行分析,從而判斷系統的穩定性;
通常來說:閉環系統的閉環傳遞函數的極點都在S平面的左半平面,則系統穩定;
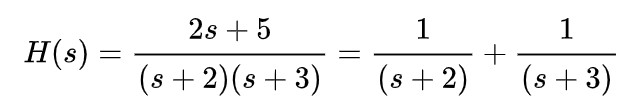
所以極點為-2,-3,在左半平面,所以系統穩定;
這里和時域上穩定性的結論如何聯系起來呢?
經過拉普拉斯反變換:
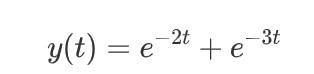
在這里不難發現,從時域的角度看,當,收斂;
所以閉環傳遞函數的極點位置在S平面的左半平面,系統穩定;
根據零極點判斷系統穩定性的方法還有以下幾種;
勞斯穩定性判據;
赫爾維茨穩定性判據;
伯德圖穩定性判定法(頻響);
奈奎斯特穩定性判據(頻響);
結論
簡單介紹了LTI系統,系統傳遞函數和傳遞函數的零極點定義,以及時域上系統穩定性和S域的穩定性之間的關聯;
有點難,為了頭發,暫時先到這里吧。
責任編輯:lq6
-
PID
+關注
關注
35文章
1471瀏覽量
85286 -
零點
+關注
關注
0文章
17瀏覽量
10835 -
時域
+關注
關注
1文章
71瀏覽量
28504 -
控制算法
+關注
關注
4文章
166瀏覽量
21686
原文標題:PID系統穩定性與零極點的關系
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
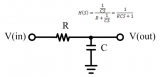
電容分別在輸入端、反饋端和輸出端,對電路的穩定性有何影響?
鳳凰動力舵輪驅動輪的穩定性如何影響AGV的運行效率和穩定性





 什么是零點和極點?時域上系統穩定性和S域的穩定性有什么關系?
什么是零點和極點?時域上系統穩定性和S域的穩定性有什么關系?











評論