直方圖線性拉伸相對于直方圖均衡化來說就更好理解一些了,即用線性變化將灰度直方圖較窄的部分拉伸至整個區間,增強整幅圖像的對比度。
線性拉伸的效果如下圖所示,可以看出圖像對比度有所改善,保留了直方圖基本的輪廓,同時將直方圖范圍拉伸至0~255。
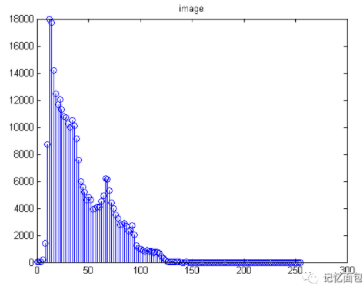

圖 1 直方圖拉伸效果圖
算法也比較容易理解,f(x,y)為輸入圖像,得到輸出圖像g(x,y)
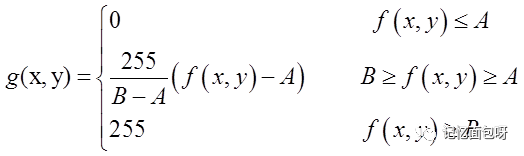
其中A和B可以分別定義為圖像的最小灰度值與最大灰度值,即
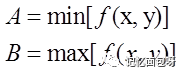
但是實際應用中并不會直接采用上述的A和B,這是由于圖像中可能存在噪聲的原因。想象如果圖像中存在幾個純白點(255)和純黑點(0),那么拉伸后的效果就無法達到預期。
因此我們人為的設定兩個閾值Thr_Min和Thr_Max,拉伸系數A,B定義如下:

其中∑H(k)為灰度直方圖累計和。下圖更直觀的表示了A和B的取值,Thr_ Min和Thr_Max是藍色部分的面積。

圖 2 A,B系數的定義
系統框架
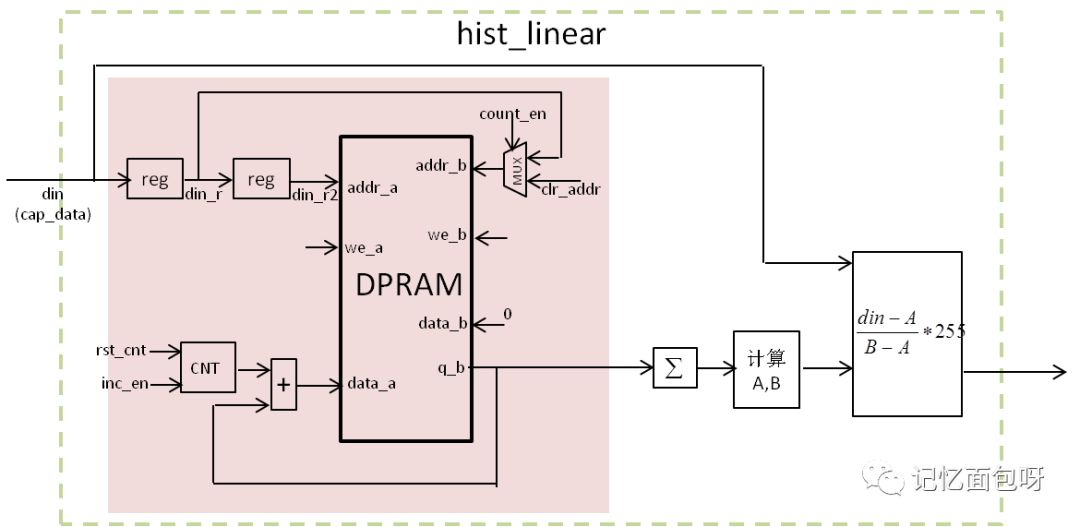
圖 3 直方圖線性拉伸系統框架
上圖可以看出,前半部分的直方圖統計電路和上篇均衡化完全一樣,只是對后半部分的電路做了些修改。計算直方圖線性拉伸后的像素值的步驟如下:
1. 統計第一幀圖像的灰度直方圖
2. 計算直方圖累計和
3. 由閾值Thr_Min和Thr_Max算出拉伸系數A,B
4. 第二幀圖像灰度值帶入公式計算后輸出
和直方圖均衡化一樣,這里我們不考慮幀緩存的問題,也就是前一幀的A,B作為當前幀A,B來使用。
代碼分析
A,B系數的計算
hist_cnt為計算出的累計和(與直方圖均衡化中的求法一樣),當累計和大于閾值的時候,記錄下此時累計和對應的地址out_pixel[8:1](即灰度值),作為我們的拉伸系數A,B,同時設置取得系數標志get_max或get_min為1。最后要在第二幀累計和到來時,清零A,B及get標志。

2. B-A的計算
取得系數B后(get_max=1),即可計算出B-A 。
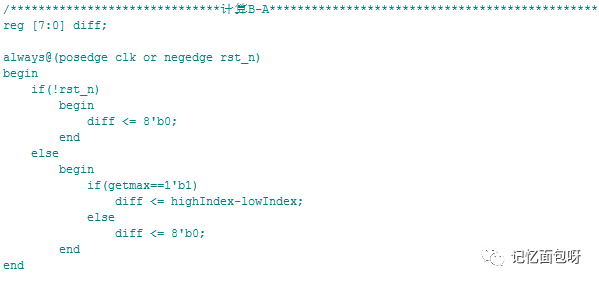
3. f(x,y)-A (第一級流水)
當f(x,y)小于系數A時,直接令f(x,y)-A=0;當f(x,y)大于系數B時,直接令f(x,y)-A=B-A。

4. [f(x,y)-A ]*255 (第二級流水)

5. [f(x,y)-A ]*255/(B-A) (第三級流水)

實驗結果


圖 4 原圖 圖 5 閾值為100時處理后的圖像
有沒有覺得這兩幅圖并沒有什么差別,之前有提到過噪聲可能對直方圖線性拉伸的影響,下面是將閾值Thr_Min調高至1000后得到的結果。

圖 6 閾值為1000時處理后的圖像
可以看出直方圖線性拉伸需要人為的調整閾值的大小,才能達到理想效果。而直方圖均衡化則不需要。
文章出處:【微信公眾號:FPGA之家】
責任編輯:gt
-
FPGA
+關注
關注
1626文章
21678瀏覽量
602001 -
噪聲
+關注
關注
13文章
1118瀏覽量
47372
原文標題:基于FPGA灰度直方圖線性拉伸
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
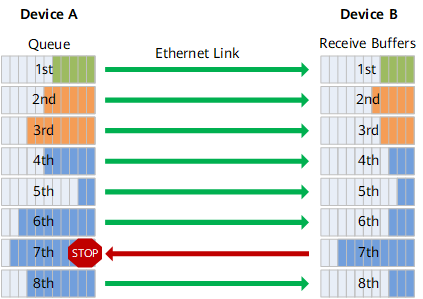
RoCE與IB對比分析(二):功能應用篇
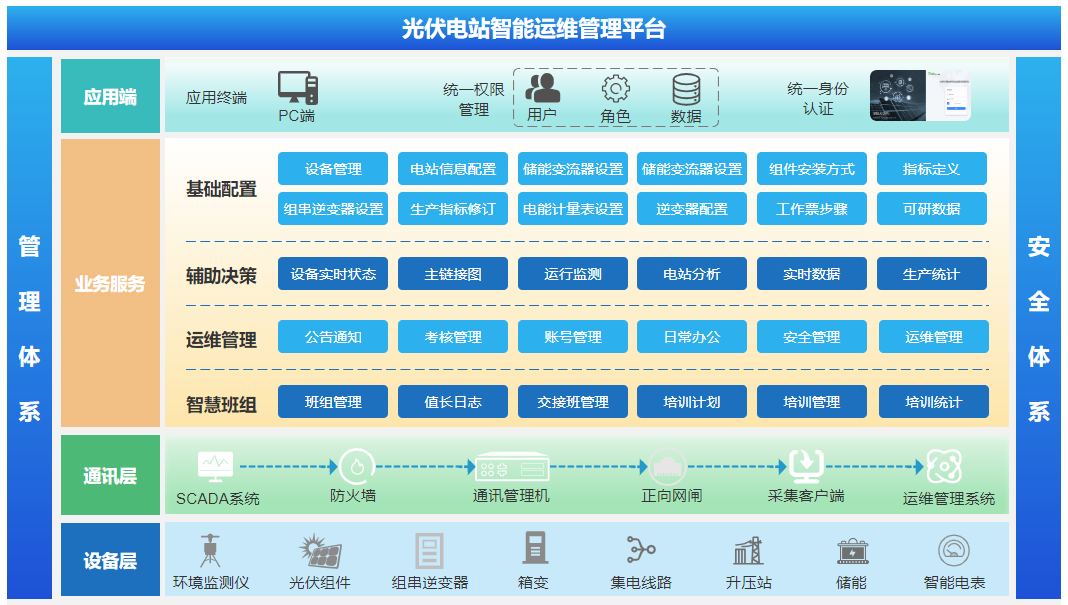
光伏電站運維管理系統與傳統運維模式對比分析
常用音頻線接口對比分析
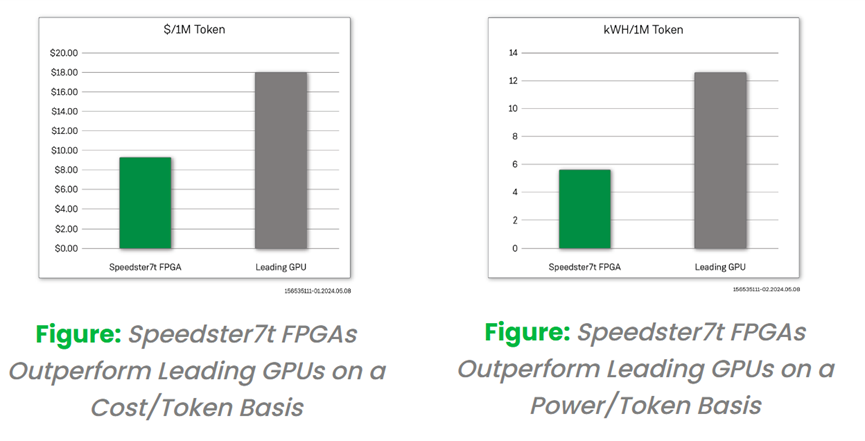
Achronix Speedster7t FPGA與GPU解決方案的比較
對比分析點焊機與傳統焊接方法
網關和路由器的對比分析
交流伺服電機與直流伺服電機的對比分析
超級電容儲能與飛輪儲能的對比分析
DC電源模塊與AC電源模塊的對比分析





 基于FPGA的直方圖線性拉伸的解決方案與對比分析
基于FPGA的直方圖線性拉伸的解決方案與對比分析











評論