關于CNN，

第1部分：卷積神經網絡的介紹

CNN是什么？：它們如何工作，以及如何在Python中從頭開始構建一個CNN。

在過去的幾年里，卷積神經網絡（CNN）引起了人們的廣泛關注，尤其是因為它徹底的改變了計算機視覺領域。在這篇文章中，我們將以神經網絡的基本背景知識為基礎，探索什么是CNN，了解它們是如何工作的，并在Python中從頭開始構建一個真正的CNN（僅使用numpy）。

準備好了嗎？讓我們開看看吧

1. 動機

CNN的經典用例是執行圖像分類，例如查看寵物的圖像并判斷它是貓還是狗。這看起來是一個簡單的任務，那為什么不使用一個普通的神經網絡呢？

好問題！

原因1：圖像很大

現在用于計算機視覺問題的圖像通常是224x224或更大的。想象一下，構建一個神經網絡來處理224x224彩色圖像：包括圖像中的3個彩色通道（RGB），得到224×224×3 = 150，528個輸入特征！在這樣的網絡中，一個典型的隱含層可能有1024個節點，因此我們必須為第一層單獨訓練150，528 x 1024 = 1.5 +億個權重。我們的網絡將是巨大的，幾乎不可能訓練的。

我們也不需要那么多權重。圖像的好處是，我們知道像素在相鄰的上下文中最有用。圖像中的物體是由小的局部特征組成的，比如眼睛的圓形虹膜或一張紙的方角。從第一個隱藏層中的每個節點來說，查看每個像素看起來不是很浪費嗎？

原因二：立場可以改變

如果你訓練一個網絡來檢測狗，你希望它能夠檢測狗，不管它出現在圖像的什么地方。想象一下，訓練一個網絡，它能很好地處理特定的狗的圖像，然后為它提供相同圖像的略微移位的版本。狗不會激活相同的神經元，因此網絡會有完全不同的反應！

我們很快就會看到CNN如何幫助我們解決這些問題。

2.數據集

在這篇文章中，我們將解決計算機視覺的“Hello，World！”：MNIST手寫數字分類問題。這很簡單：給定圖像，將其分類為數字。

MNIST數據集中的每個圖像都是28x28，并包含了一個以中心為中心的灰度數字。

說實話，一個正常的神經網絡實際上可以很好地解決這個問題。你可以將每個圖像視為一個28x28 = 784維的向量，將其提供給一個784-dim的輸入層，堆疊幾個隱藏層，最后的輸出層包含10個節點，每個數字對應一個節點。

因為MNIST數據集包含小圖像居中，所以我們不會遇到上述的大小或移動問題。然而，在這篇文章的整個過程中請記住，大多數現實世界中的圖像分類問題并沒有這么簡單。

那么，現在你已經有足夠的積累了。讓我們正式進入CNN的世界！

3.卷積

什么是卷積神經網絡？

它們基本上只是使用卷積層的神經網絡，即基于卷積數學運算的Conv層。Conv圖層由一組濾鏡組成，你可以將其看作是數字的二維矩陣。這里有一個例子3x3過濾器：

我們可以使用一個輸入圖像和一個過濾器通過將過濾器與輸入圖像進行卷積來生成一個輸出圖像。這包括

將過濾器覆蓋在圖像的某個位置上。

在過濾器中的值與其在圖像中的對應值之間執行元素級乘法。

總結所有元素產品。這個和是輸出圖像中目標像素的輸出值。

對所有位置重復。

旁注：我們（以及許多CNN實現）實際上在技術上使用的是互相關而不是卷積，但它們做的幾乎是一樣的。我不會在這篇文章中詳細討論它們之間的區別，因為這并不重要。

這四步描述有點抽象，我們來做個例子。看下這個微小的4x4灰度圖像和這個3x3濾鏡：

圖像中的數字表示像素強度，其中0為黑色，255為白色。我們將卷積輸入圖像和過濾器產生一個2x2輸出圖像：

3.1這有什么用？

讓我們縮小一下，在更高的層次上看這個。將圖像與過濾器進行卷積會做什么？我們可以從我們一直使用的例子3x3過濾器開始，它通常被稱為垂直Sobel過濾器：

Sobel過濾器是一種邊緣檢測器。垂直Sobel過濾器檢測垂直邊緣，水平Sobel過濾器檢測水平邊緣。輸出圖像現在很容易解釋：輸出圖像中的亮像素（高值像素）表示在原始圖像中有一個強邊緣。

你能看出為什么邊緣檢測圖像可能比原始圖像更有用嗎？回想一下我們的MNIST手寫數字分類問題。在MNIST上訓練的CNN可以尋找數字1，例如，通過使用邊緣檢測過濾器并檢查圖像中心附近的兩個突出的垂直邊緣。通常，卷積有助于我們查找特定的本地化圖像特征（如邊緣），我們可以在以后的網絡中使用。

3.2填充

還記得以前將4x4輸入圖像與3x3濾波器卷積得到2x2輸出圖像嗎？通常，我們希望輸出圖像與輸入圖像的大小相同。為此，我們在圖像周圍添加零，這樣我們就可以在更多的地方覆蓋過濾器。一個3x3的過濾器需要1像素的填充：

這稱為“相同”填充，因為輸入和輸出具有相同的尺寸。不使用任何填充，這是我們一直在做的，并將繼續為這篇文章做，有時被稱為“有效”填充。

3.3 Conv層（Conv Layers）

現在我們知道了圖像卷積是如何工作的以及它為什么有用，讓我們看看它在CNN中的實際應用。如前所述，CNN包括conv層，它使用一組過濾器將輸入圖像轉換為輸出圖像。conv層的主要參數是它擁有的過濾器的數量。

對于MNIST CNN，我們將使用一個帶有8個過濾器的小conv層作為網絡的初始層。這意味著它將把28x28的輸入圖像轉換成26x26x8的容量：

提醒：輸出是26x26x8，而不是28x28x8，因為我們使用了有效的填充，這將輸入的寬度和高度降低了2。

conv層中的4個過濾器每個都產生一個26x26的輸出，因此它們疊加在一起構成一個26x26x8。所有這些都是因為3×3（過濾器大小） × 8（過濾器數量）= 72個權重！

3.4實施卷積

是時候把我們學到的東西寫進代碼里了！我們將實現conv層的前饋部分，它負責將過濾器與輸入圖像進行卷積以生成輸出卷。為了簡單起見，我們假設過濾器總是3x3（這并不是真的，5x5和7x7過濾器也很常見）。

讓我們開始實現一個conv層類：

Conv3x3類只接受一個參數：過濾器的數量。在構造函數中，我們存儲過濾器的數量，并使用NumPy的randn（）方法初始化一個隨機過濾器數組。

注意：如果初始值過大或過小，訓練網絡將無效。

接下來，實際的卷積：

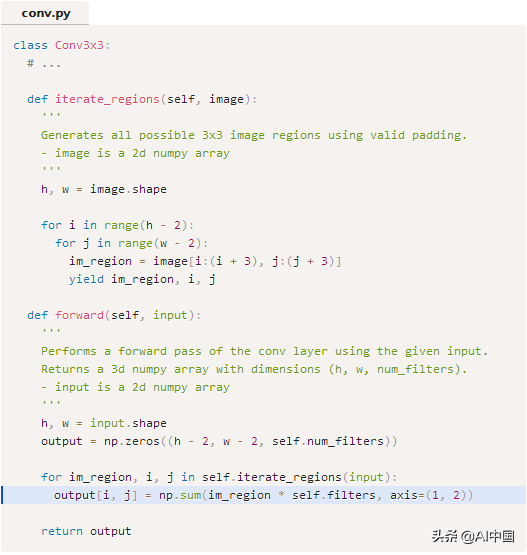
iterate_regions（）是一個輔助發生器的方法，收益率為我們所有有效3 x3的圖像區域。這對于以后實現該類的向后部分非常有用。

上面突出顯示了實際執行卷積的代碼行。讓我們來分解一下：

我們有im_region，一個包含相關圖像區域的3x3數組。

我們有self.filters，一個3d數組。

我們做im_region * self.filters，它使用numpy的廣播機制以元素方式乘以兩個數組。結果是一個3d數組，其尺寸與self.filters相同。

我們np.sum（）上一步的結果使用axis =（1，2），它產生一個長度為num_filters的1d數組，其中每個元素包含相應過濾器的卷積結果。

我們將結果分配給輸出［i，j］，其中包含輸出中像素（i，j）的卷積結果。

對輸出中的每個像素執行上面的序列，直到得到最終的輸出卷為止！讓我們測試一下我們的代碼：

目前看起來不錯。

注意：在Conv3x3實現中，為了簡單起見，我們假設輸入是一個2d numpy數組，因為MNIST圖像就是這樣存儲的。這對我們有用，因為我們使用它作為我們網絡的第一層，但大多數cnn有更多的Conv層。如果我們要構建一個更大的網絡，需要多次使用Conv3x3，那么我們必須將輸入設置為3d numpy數組。

4. 池化

圖像中的相鄰像素往往具有相似的值，因此conv層通常也會為輸出中的相鄰像素生成相似的值。因此，conv層輸出中包含的大部分信息都是多余的。例如，如果我們使用邊緣檢測過濾器，并在某個位置找到一個強邊緣，那么我們很可能也會在距離原始位置1像素的位置找到一個相對較強的邊緣。然而，這些都是相同的邊緣！我們沒有發現任何新東西。

池化層解決了這個問題。他們所做的就是減少（通過猜測）在輸入中匯總值的輸入大小。池化層通常由一個簡單的操作完成，比如max、min或average。

為了執行最大池化，我們在2x2塊中輸入了圖像（因為池的大小= 2），并將最大值放入對應像素處的輸出圖像中。就是這樣！

它將輸入的寬度和高度除以它的大小。對于MNIST CNN，我們將在初始conv層之后放置一個池大小為2的最大池化層。池化層將26x26x8輸入轉換為13x13x8輸出：

4.1 Implementing Pooling（實施池）

我們將實現一個MaxPool2類與我們的conv類相同的方法從上一節：

這個類的工作原理類似于我們之前實現的Conv3x3類。關鍵行再次突出顯示：要從給定的圖像區域找到最大值，我們使用np.amax（）， numpy的array max方法。我們設置axis=（0，1），因為我們只想最大化前兩個維度（高度和寬度），而不是第三個維度（num_filters）。

我們來試試吧！

我們的MNIST CNN開始走到一起了！

5. Softmax

為了完成我們的CNN，我們需要賦予它實際預測的能力。我們將通過使用一個多類分類問題的標準最終層來實現這一點：Softmax層，這是一個使用Softmax激活函數的標準全連接（密集）層。

提醒：全連接層的每個節點都連接到上一層的每個輸出。如果你需要復習的話，我們在介紹神經網絡時使用了全連接層圖層。

Softmax將任意實值轉換為概率。它背后的數學原理很簡單：給定一些數字，

取e（數學常數）的每一次方。

把所有的指數（eee的冪）加起來。這個結果是分母。

用每個數的指數作為它的分子。

概率= Numerator/Denominator

寫得更妙的是，Softmax對nnn數字執行以下轉換X1.。.Xn：

Softmax變換的輸出總是在［0，1］［0，1］［0，1］［0，1］范圍內，并且加起來等于1，由此轉換成概率。

下面是一個使用數字-1、0、3和5的簡單例子：

5.1使用方法

我們將使用一個包含10個節點的softmax層，每個節點代表一個數字，作為CNN的最后一層。層中的每個節點都將連接到每個輸入層。應用softmax變換后，以概率最高的節點表示的數字為CNN的輸出！

5.2交叉熵損失函數

你可能會想，為什么要把輸出轉化為概率呢？最高的產值不總是有最高的概率嗎？如果你這么做了，你絕對是對的。我們實際上不需要使用softmax來預測一個數字，而我們只需要從網絡中選擇輸出最高的數字即可！

softmax真正做的是幫助我們量化我們對預測的確定程度，這在訓練和評估CNN時非常有用。更具體地說，使用softmax允許我們使用交叉熵損失函數，它考慮到我們對每個預測的確定程度。下面是我們計算交叉熵損失函數的方法：

c在哪里是正確的類（在我們的例子中是正確的數字），Pc類c的預測概率，并在natural log中。一如既往的，損失越少越好。例如，在最好的情況下，我們會

在更現實的情況下，我們可能會有

我們將在稍后的文章中再次看到交叉熵損失函數，所以請記住這一點！

5.3實施Softmax

你現在知道這個練習，讓我們實現一個Softmax圖層類

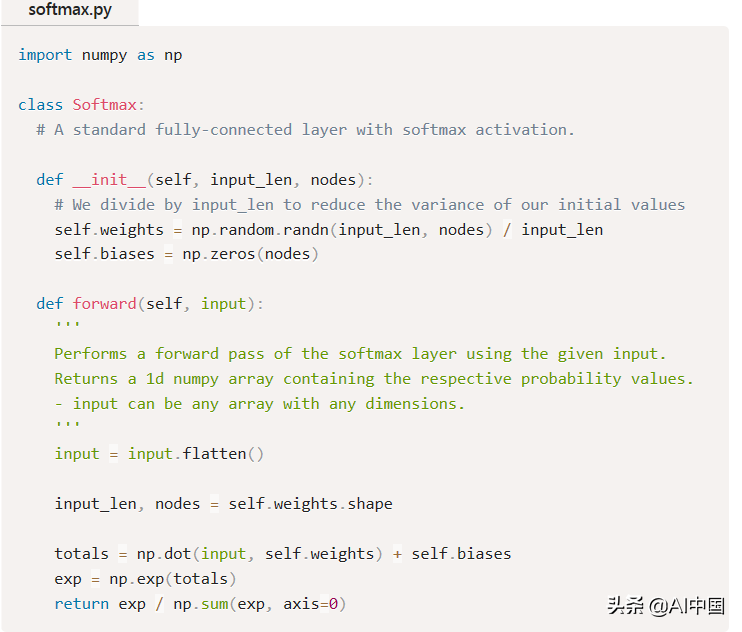
這里沒有什么太復雜的。幾個亮點：

我們將輸入壓平（），使其更容易處理，因為我們不再需要它的形狀。

np.dot（）將輸入和self相乘。按元素加權，然后對結果求和。

np.exp（）計算用于Softmax的指數。

我們現在已經完成了CNN的整個轉發！放在一起：

運行cnn.py給我們輸出類似于：

這是有道理的：使用隨機權重初始化，你會期望CNN只會像隨機猜測一樣好。隨機猜測的話，10%的準確率（因為有10類）和一個叉的損失?ln?（0.1） = 2.302 {- ln （0.1）} = 2.302?ln（0.1） = 2.302，這是我們得到的！

想自己嘗試或修改這段代碼嗎？在瀏覽器中運行CNN。它也可以在Github上使用。

6. 結論

以上就是對CNN的介紹！在這篇文章中，我們

為什么CNN在某些問題上可能更有用，比如圖像分類。

介紹MNIST手寫數字數據集。

了解Conv層，它將過濾器與圖像進行卷積以產生更有用的輸出。

談到了池化層，它可以幫助刪除除最有用的功能之外的所有功能。

實現了一個Softmax層，因此我們可以使用交叉熵損失。

還有很多東西我們還沒有講到，比如如何訓練CNN。本系列的第2部分將對CNN進行深入的一個訓練，包括推導梯度和實施反向傳播。

編輯：jq