前言

在圖論中，在尋路最短路徑中除了Dijkstra算法以外，還有Floyd算法也是非常經(jīng)典，然而兩種算法還是有區(qū)別的，Floyd主要計算多源最短路徑。

在單源正權值最短路徑，我們會用Dijkstra算法來求最短路徑，并且算法的思想很簡單—貪心算法:每次確定最短路徑的一個點然后維護(更新)這個點周圍點的距離加入預選隊列，等待下一次的拋出確定。雖然思想很簡單，實現(xiàn)起來是非常復雜的，我們需要鄰接矩陣(表)儲存長度，需要優(yōu)先隊列(或者每次都比較)維護一個預選點的集合。還要用一個boolean數(shù)組標記是否已經(jīng)確定、還要……

總之，Dijkstra算法的思想上是很容易接受的，但是實現(xiàn)上其實是非常麻煩的。但是單源最短路徑解算暫時還沒有有效的辦法，復雜度也為O(n2)。

而在n點圖中想求多源最短路徑,如果從Dijkstra算法的角度上，需要將Dijkstra執(zhí)行n次才能獲得所有點之間的最短路徑，不過執(zhí)行n次Dijkstra算法即可,復雜度為O(n3)。但是這樣感覺很臃腫，代碼量巨大，占用很多空間內(nèi)存。有沒有啥方法能夠稍微變變口味呢？

答案是有的，今天就帶大家一起了解一下牛逼轟轟的Floyed算法。

算法介紹

什么是Floyed算法？

Floyd算法又稱為插點法，是一種利用動態(tài)規(guī)劃的思想尋找給定的加權圖中多源點之間最短路徑的算法，與Dijkstra算法類似。該算法名稱以創(chuàng)始人之一、1978年圖靈獎獲得者、斯坦福大學計算機科學系教授羅伯特·弗洛伊德命名。

簡單的來說，算法的主要思想是動態(tài)規(guī)劃(dp)，而求最短路徑需要不斷松弛(熟悉spfa算法的可能熟悉松弛)。

而算法的具體思想為：

1 .鄰接矩陣(二維數(shù)組)dist儲存路徑，數(shù)組中的值開始表示點點之間初始直接路徑，最終是點點之間的最小路徑，有兩點需要注意的，第一是如果沒有直接相連的兩點那么默認為一個很大的值(不要因為計算溢出成負數(shù))，第二是自己和自己的距離要為0。

2 .從第1個到第n個點依次加入松弛計算，每個點加入進行試探枚舉是否有路徑長度被更改(自己能否更新路徑)。順序加入(k枚舉)松弛的點時候，需要遍歷圖中每一個點對(i,j雙重循環(huán))，判斷每一個點對距離是否因為加入的點而發(fā)生最小距離變化，如果發(fā)生改變(變小)，那么兩點(i,j)距離就更改。

2 .重復上述直到最后插點試探完成。

其中第2步的狀態(tài)轉(zhuǎn)移方程為:

dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])

其中dp[a][b]的意思可以理解為點a到點b的最短路徑,所以dp[i][k]的意思可以理解為i到k的最短路徑dp[k][j]的意思為k到j的最短路徑.

咱們圖解一個案例，初始情況每個點只知道和自己直接相連的點的距離，而其他間接相連的點還不知道距離，比如A-B=2,A-C=3但是B-C在不經(jīng)過計算的情況是不知道長度的。

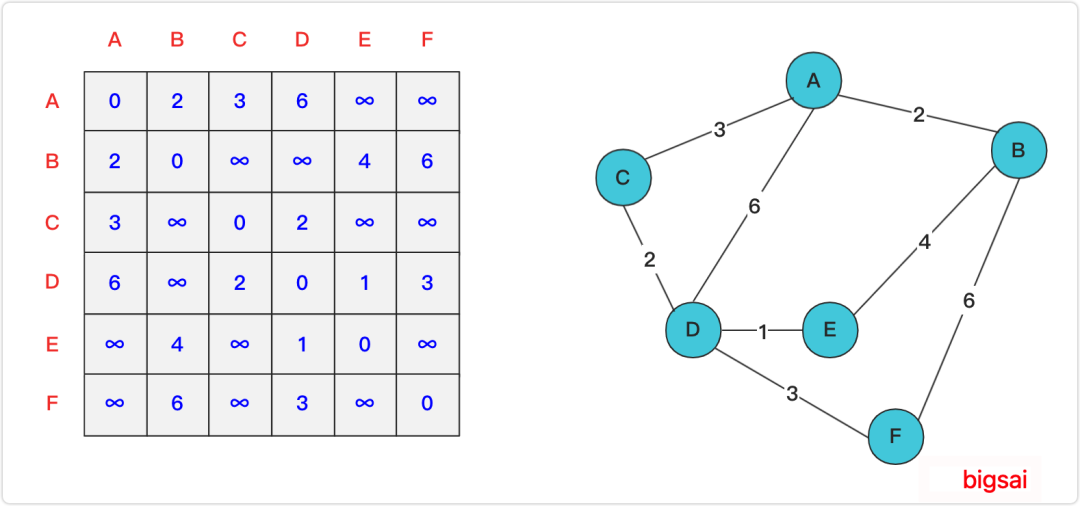
加入第一個節(jié)點A進行更新計算,大家可以發(fā)現(xiàn)，由于A的加入，使得本來不連通的B，C點對和B，D點對變得聯(lián)通，并且加入A后距離為當前最小,同時你可以發(fā)現(xiàn)加入A其中也使得C-D多一條聯(lián)通路徑（6+3），但是C-D聯(lián)通的話距離為9遠遠大于本來的(C,D)聯(lián)通路徑2，所以這條不進行更新。

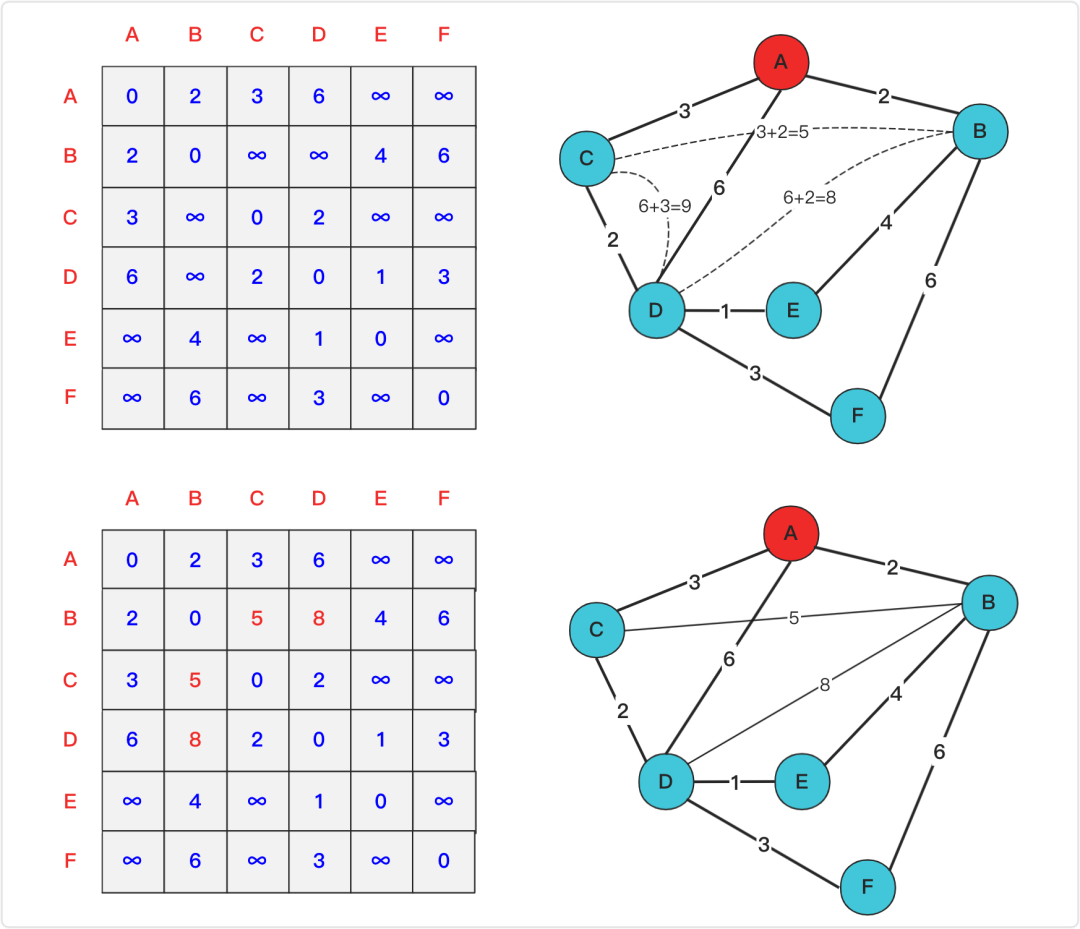
咱們繼續(xù)加入第二個節(jié)點B，這個點執(zhí)行和前面A相同操作進行。對一些點進行更新。因為和B相連的點比較多，可以產(chǎn)生很多新的路徑，這里給大家列舉一下并做一個說明,這里新路徑我統(tǒng)一用1表示，原來長度用0表示。

AF1=AB+BF=6+2=8 < AF0(∞) 進行更新

AE1=AB+BE=2+4=6 < AE0(∞) 進行更新

CE1=CB+BE=5+5=9 < CE0(∞) 進行更新

CF1=CB+BF=5+6=11

EF1=EB+BF=4+6=10

當然，也有一些新的路徑大于已有路徑不進行更新，例如：

AC1=AB+BC=2+5=7>AC0(3)不更新

AD1=AB+BD=2+8=10>AD0(6)不更新

……

更多路徑這里就不一一列舉了。

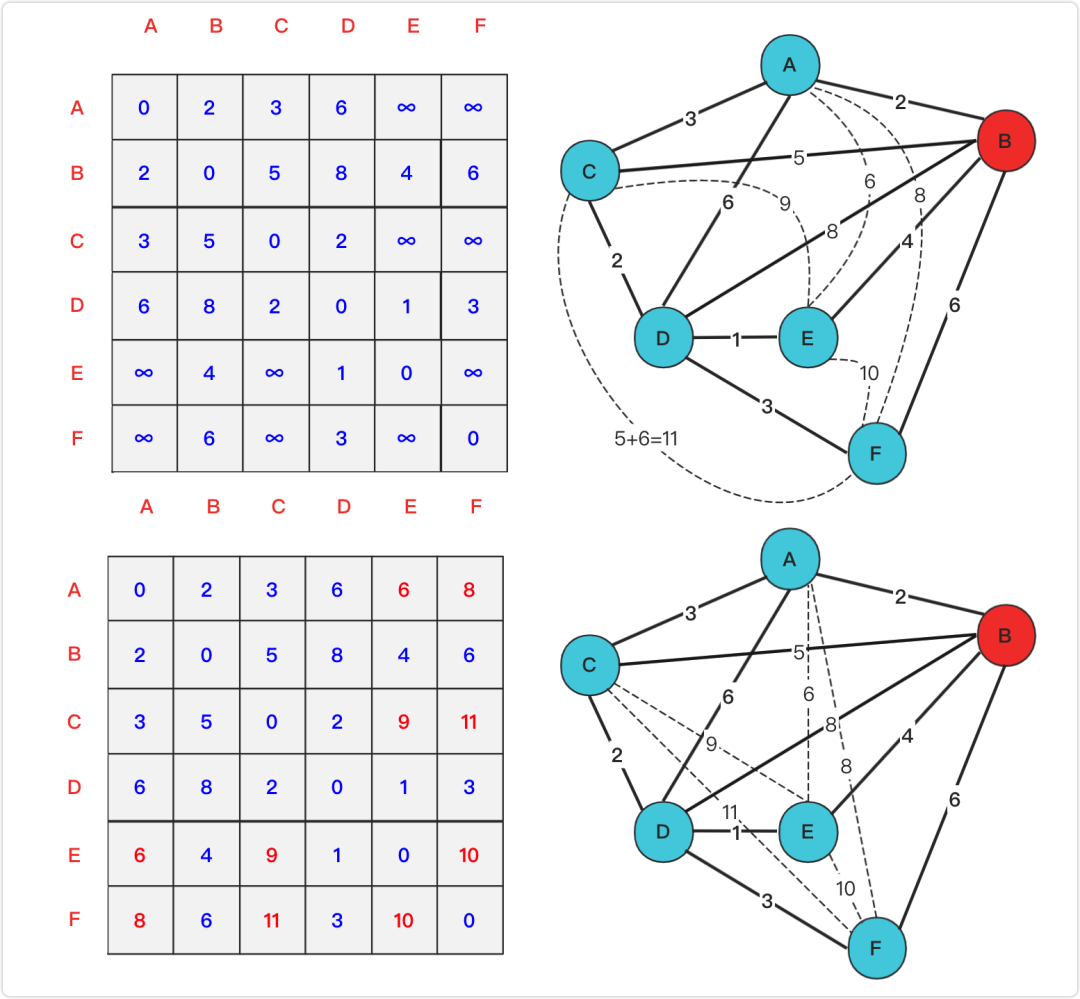
后序加入C、D、E、F都是進行相同的操作,最終全部加完沒有路徑可以更新就結(jié)束停止。實際上這個時候圖中的連線就比較多了。這些連線都是代表當前的最短路徑。這也和我們的需求貼合，我們最終要的是所有節(jié)點的最短路徑。每個節(jié)點最終都應該有5條指向不同節(jié)點的邊！矩陣對應邊值就是點點之間最短路徑。

至于算法的模擬兩部核心已經(jīng)告訴大家了，大家可以自行模擬剩下的。

程序?qū)崿F(xiàn)

而對于程序而言，這個插入的過程相當簡單。核心代碼只有四行！這個寫法適合有向圖和無向圖，無向圖的算法優(yōu)化后面會說。
代碼如下

publicclassfloyd{
staticintmax=66666;//別Intege.max兩個相加越界為負
publicstaticvoidmain(String[]args){
intdist[][]={
{0,2,3,6,max,max},
{2,0,max,max,4,6},
{3,max,0,2,max,max},
{6,max,2,0,1,3},
{max,4,max,1,0,max},
{max,6,max,3,max,0}};//地圖
//6個
for(intk=0;k6;k++)//加入第k個節(jié)點進行計算
{
for(inti=0;i6;i++)//每加入一個點都要枚舉圖看看有沒有可以被更新的
{
for(intj=0;j6;j++)
{
dist[i][j]=Math.min(dist[i][j],dist[i][k]+dist[k][j]);
}
}
}
//輸出
for(inti=0;i6;i++){
System.out.print("節(jié)點"+(i+1)+"的最短路徑");
for(intj=0;j6;j++){
System.out.print(dist[i][j]+"");
}
System.out.println();
}
}
}

執(zhí)行結(jié)果為：

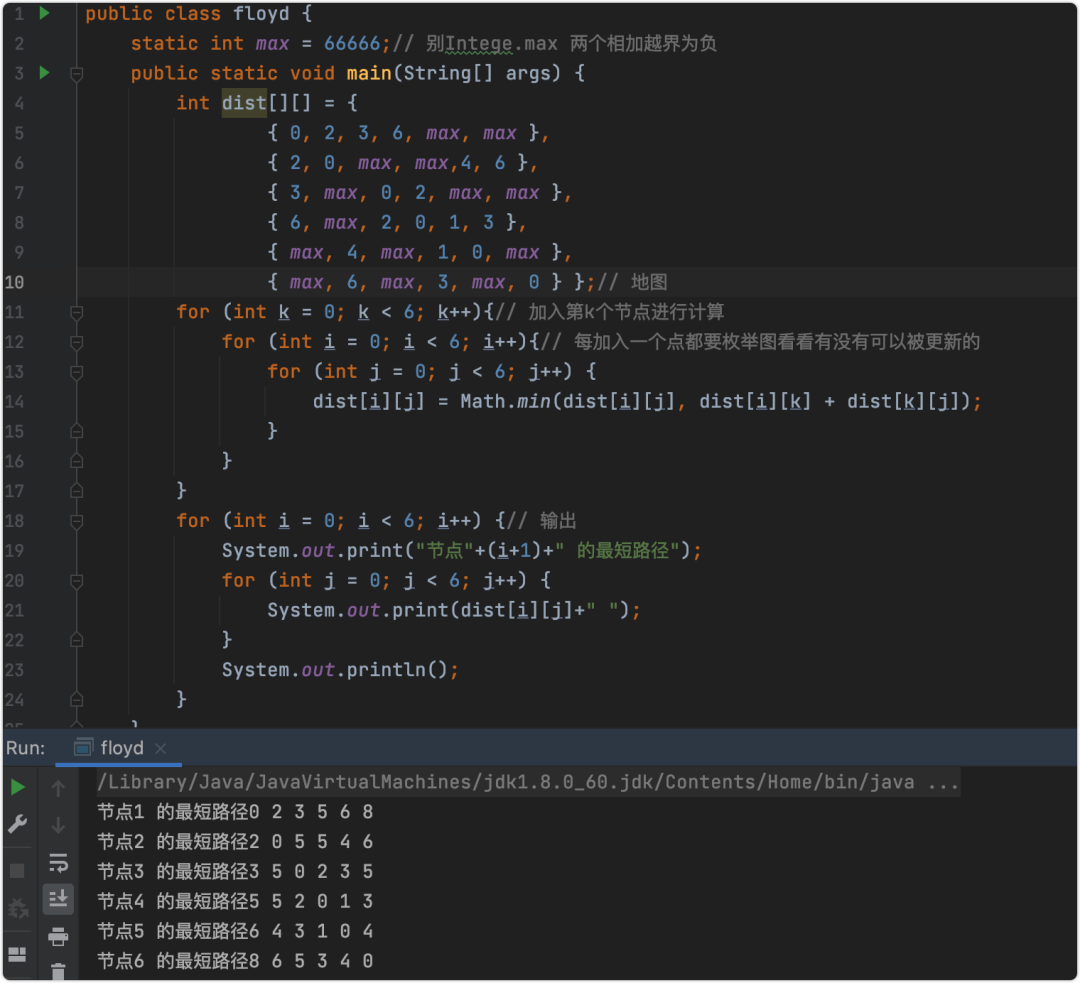
可以自行計算，圖和上篇的Dijkstra用的圖是一致的，大家可以自行比對，結(jié)果一致，說明咱么的結(jié)果成功的。

當然，在你學習的過程中，可以在每加入一個節(jié)點插入完成后，打印鄰接矩陣的結(jié)果，看看前兩部和筆者的是否相同(有助于理解)，如果相同，則說明正確！

對于加入點更新你可能還是有點疑惑其中的過程，那咱么就用一個局部來演示一下幫助你進一步理解Floyd算法，看其中AB最短距離變化情況祝你理解：

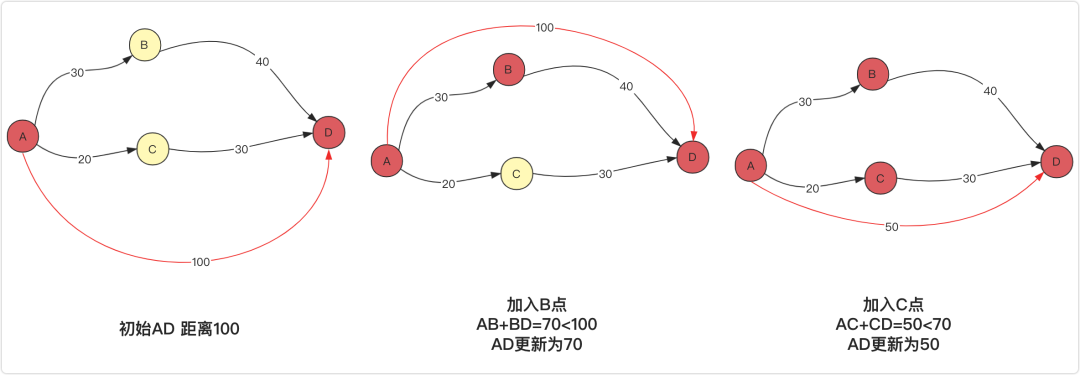
小試牛刀

自己會沒會？刷一道題就可以知道了，剛好力扣1334是一道Floyd算法解決的問題。

題目描述為：

有 n 個城市，按從 0 到 n-1 編號。給你一個邊數(shù)組 edges，其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 兩個城市之間的雙向加權邊，距離閾值是一個整數(shù) distanceThreshold。

返回能通過某些路徑到達其他城市數(shù)目最少、且路徑距離 最大 為 distanceThreshold 的城市。如果有多個這樣的城市，則返回編號最大的城市。

注意，連接城市 i 和 j 的路徑的距離等于沿該路徑的所有邊的權重之和。

示例1：

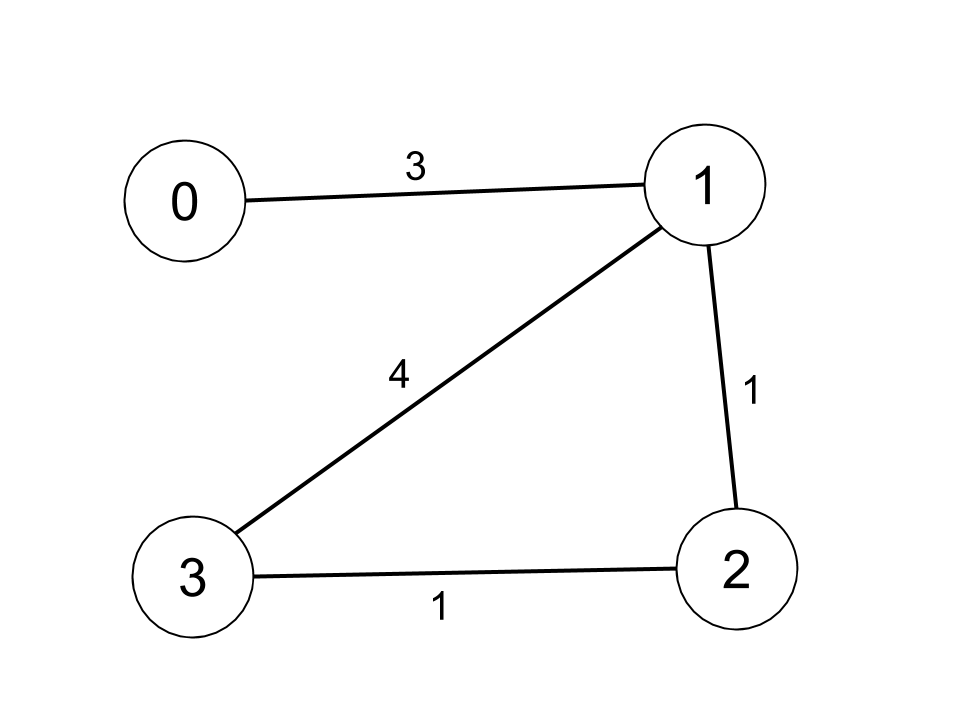
輸入：n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
輸出：3
解釋：城市分布圖如上。
每個城市閾值距離 distanceThreshold = 4 內(nèi)的鄰居城市分別是：
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在閾值距離 4 以內(nèi)都有 2 個鄰居城市，但是我們必須返回城市 3，因為它的編號最大。

示例2：

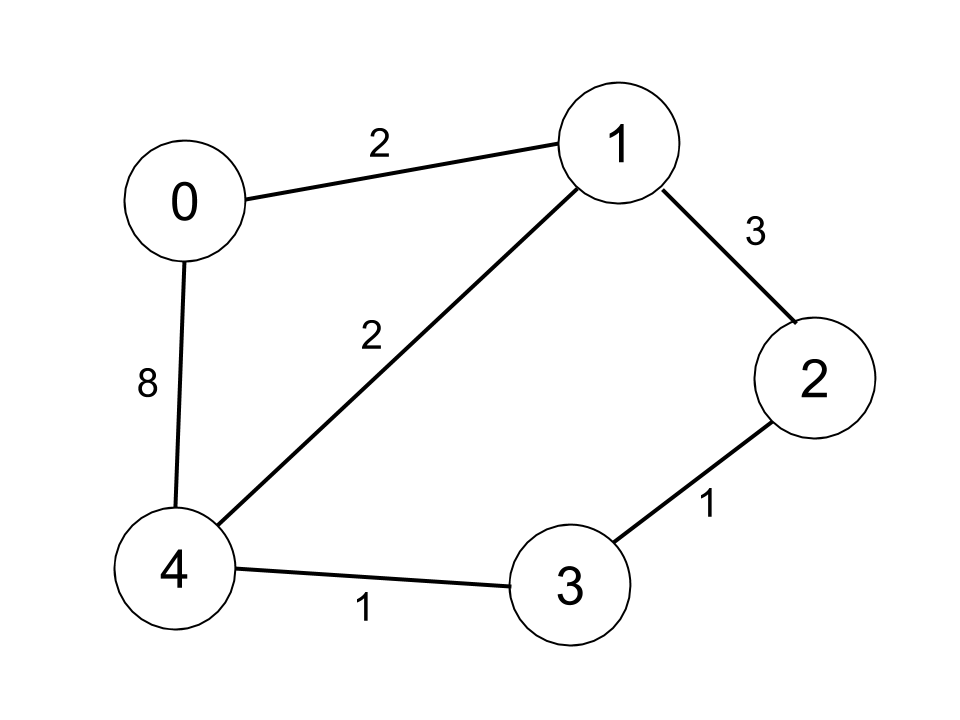
輸入：n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
輸出：0
解釋：城市分布圖如上。
每個城市閾值距離 distanceThreshold = 2 內(nèi)的鄰居城市分別是：
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在閾值距離 2 以內(nèi)只有 1 個鄰居城市。

提示：

2 <= n <= 100
1 <= edges.length <= n * (n - 1) / 2
edges[i].length == 3
0 <= fromi < toi < n
1 <= weighti, distanceThreshold <= 10^4
所有 (fromi, toi) 都是不同的。

思路分析：

拿到一道題，首先就是要理解題意，而這道題的意思借助案例也是非常能夠理解，其實就是判斷在distanceThreshold范圍內(nèi)找到能夠到達的最少點的編號，如果多個取最大即可。正常求到達最多情景比較多這里求的是最少的，但是思路都是一樣的。

這道題如果使用搜索，那復雜度就太高了啊，很明顯要使用多源最短路徑Floyd算法，具體思路為;

1 .先使用Floyd算法求出點點之間的最短距離，時間復雜度O(n3)

2 . 統(tǒng)計每個點與其他點距離在distanceThreshold之內(nèi)的點數(shù)量，統(tǒng)計的同時看看是不是小于等于已知最少個數(shù)的，如果是，那么保存更新。

3 .返回最終的結(jié)果。

實現(xiàn)代碼：

classSolution{
publicintfindTheCity(intn,int[][]edges,intdistanceThreshold){
intdist[][]=newint[n][n];
for(inti=0;ifor(intj=0;j//保證數(shù)據(jù)比最大二倍大(兩相加不能比它大)，并且不能溢出，不要Int最大相加為負會出錯
dist[i][j]=1000000;
}
dist[i][i]=0;
}
for(intarr[]:edges){
dist[arr[0]][arr[1]]=arr[2];
dist[arr[1]][arr[0]]=arr[2];
}
for(intk=0;kfor(inti=0;ifor(intj=0;jintmin=Integer.MAX_VALUE;
intminIndex=0;
intpathNum[]=newint[n];//存儲距離
for(inti=0;ifor(intj=0;jif(dist[i][j]<=distanceThreshold){
????????????????????pathNum[i]++;
????????????????}
????????????}
????????????if(pathNum[i]<=min)?{
????????????????min?=?pathNum[i];
????????????????minIndex=i;
????????????}
????????}
????????returnminIndex;

}
}

那么想一下優(yōu)化空間：Floyd算法還有優(yōu)化空間嘛？

有的，這個是個無向圖，也就是加入點的時候枚舉其實會有一個重復的操作過程(例如枚舉AC和CA是效果一致的)，所以我們在Floyd算法的實現(xiàn)過程中過濾掉重復的操作，具體代碼為：

classSolution{
publicintfindTheCity(intn,int[][]edges,intdistanceThreshold){
intdist[][]=newint[n][n];//存儲距離
for(inti=0;ifor(intj=0;j1000000;
}
dist[i][i]=0;
}
for(intarr[]:edges){
dist[arr[0]][arr[1]]=arr[2];
dist[arr[1]][arr[0]]=arr[2];
}
for(intk=0;kfor(inti=0;ifor(intj=i+1;j//去掉重復的計算
dist[i][j]=Math.min(dist[i][j],dist[i][k]+dist[k][j]);
dist[j][i]=dist[i][j];
}
}
}
intmin=Integer.MAX_VALUE;
intminIndex=0;
intpathNum[]=newint[n];//
for(inti=0;ifor(intj=0;jif(dist[i][j]<=distanceThreshold){
????????????????????pathNum[i]++;
????????????????}
????????????}
????????????if(pathNum[i]<=min)?{
????????????????min?=?pathNum[i];
????????????????minIndex=i;
????????????}
????????}
????????returnminIndex;

}
}

尾聲

對于Floyd算法，如果初次接觸不一定能夠理解這個松弛的過程。

Floyd像什么呢，最終最短路徑大部分都是通過計算得到而存儲下來直接使用的，我覺得它和MySQL視圖有點像的，視圖是一個虛表在實表上計算獲得的，但是計算之后各個數(shù)據(jù)就可以直接使用，Floyd是在原本的路徑圖中通過一個動態(tài)規(guī)劃的策略計算出來點點之間的最短路徑。

Floyd和Dijkstra是經(jīng)典的最短路徑算法，兩者有相似也有不同。在復雜度上，Dijkstra算法時間復雜度是O(n2),Floyd算法時間復雜度是O(n3)；在功能上，Dijkstra是求單源最短路徑，并且路徑權值不能為負，而Floyd是求多源最短路徑，可以有負權值；算法實現(xiàn)上，Dijkstra 是一種貪心算法實現(xiàn)起來較復雜，Floyd基于動態(tài)規(guī)劃實現(xiàn)簡單；兩個作者Dijkstra和Floyd都是牛逼轟轟的大人物，都是圖靈獎的獲得者。

除了Floyd算法，堆排序算法heapSort也是Floyd大佬發(fā)明的，屬實佩服！

Floyd算法，俗稱插點法，不就一個點一個點插進去更新用到被插點距離嘛！

好啦，F(xiàn)loyd算法就介紹到這里，如果對你有幫助，請動動小手點個贊吧！蟹蟹。