隨著社會的進步,人們生活水平的提高,或是人人都有私家車,然而驅車在外,停車卻成了一個頭大的問題。而沒車的我在維護一組智能停車計時器,它們提供了關于它們使用頻率和使用時間的數據。而時刻都在思考,如何才能為大家提供更好的服務。
如果可以根據儀表的過去表現,根據供求規律來預測它的未來價值,那會怎樣呢?
準確預測什么時間采取相應策略來實現目標,這是一個不小的挑戰,但對于這個挑戰,其實是可以通過時間序列預測來解決。當你們在高峰期苦苦尋找停車位時,又被告知這將收取你比平時更多的費用,你們肯定難以接受。但街道通暢無阻的話,車主停車方便,也能給我帶來不少的收入,真是一舉兩得!
接下來我們來探索一些時間序列算法。
一些定義時間序列預測法時間序列預測法是一種歷史資料延伸預測,也稱歷史引伸預測法。是以數據數列所能反映的社會經濟現象的發展過程和規律性,進行引伸外推,預測其發展趨勢的方法。
需要明確一點的是,與回歸分析預測模型不同,時間序列模型依賴于數值在時間上的先后順序,同樣大小的值改變順序后輸入模型產生的結果是不同的。
時間序列預測對商業有真正的價值,因為它直接應用于定價、庫存和供應鏈問題。雖然深度學習技術已經開始用于獲得更多的洞察力,以更好地預測未來,但時間序列預測仍然是一個主要由經典ML技術提供信息的領域。
當遇到時間序列這個詞時,你需要了解它在不同語境中的用法。
時間序列在數學中,時間序列是按時間順序索引(或列出或圖表)的一系列數據點。最常見的是,時間序列是在連續的等間隔時間點上獲得的序列。
時間序列的一個例子是道瓊斯工業平均指數[1]的日收盤價。在信號處理、天氣預報、地震預報和其他可以繪制事件和數據點的領域中,經常會遇到時間序列圖和統計建模的使用。
時間序列分析時間序列分析,就是對上述時間序列數據的分析。時間序列數據可以采取不同的形式,包括中斷時間序列,它檢測時間序列在中斷事件前后的演變模式。時間序列所需的分析類型取決于數據的性質。時間序列數據本身可以采用數字或字符序列的形式。
時間序列分析考慮了這樣一個事實,即隨著時間的推移獲取的數據點可能具有應該考慮的內部結構(例如自相關、趨勢或季節性變化)
要進行的分析使用多種方法,包括頻域和時域、線性和非線性等等。可參見了解更多關于這類數據的時間序列分析的多種方法[2]。
時間序列分解時間序列由四個部分組成:
:季節性成分
:趨勢性成分
:周期性成分
:殘差,或不規則組件。
時間序列分量分解之間的關系:
加法分解:
, 在哪里 是當時的數據 噸。
乘法分解:
將乘法關系變成加法關系:
一個加模型是否季節性波動的幅度不隨水平變化是適當的。如果季節性波動與序列的水平成正比,那么乘法模型是合適的。乘法分解在經濟序列中更為普遍。
時間序列預測時間序列預測是使用一個模型來預測未來的價值,該模型基于以前收集的數據在過去發生的模式。雖然可以使用回歸模型來探索時間序列數據,將時間指數作為圖表上的 變量,但最好使用特殊類型的模型來分析此類數據。
時間序列數據是一組有序的觀測數據,不像可以通過線性回歸分析的數據。最常見的是ARIMA,這是Autoregressive Integrated Moving Average(自回歸綜合移動平均線)的首字母縮寫。
ARIMA 模型[3] 將一系列的現值與過去的值和過去的預測誤差聯系起來。它們最適合于分析時域數據,其中數據是隨時間排序的。
后面推文將介紹使用單變量時間序列[4]構建一個ARIMA模型,該模型關注一個隨時間改變其值的變量。這類數據的一個例子是這個數據集[5],它記錄了莫納羅亞天文臺每月的二氧化碳濃度:
CO2YearMonthYearMonth
330.621975.0419751
331.401975.1319752
331.871975.2119753
333.181975.2919754
333.921975.3819755
333.431975.4619756
331.851975.5419757
330.011975.6319758
328.511975.7119759
328.411975.79197510
329.251975.88197511
330.971975.96197512
時間序列數據特征在查看時間序列數據時,為了更好地理解其模式,需要拆解某些特征。如果你想要分析“信號”包含在時間序列數據中,那么就認為這些特征是相對于“信號”的“噪聲”。此時需要通過使用一些統計技術來抵消這些特征以減少“噪音”。
時間序列數據變動存在規律性與不規律性時間序列中的每個觀察值大小,是影響變化的各種不同因素在同一時刻發生作用的綜合結果。從這些影響因素發生作用的大小和方向變化的時間特性來看,這些因素造成的時間序列數據的變動分為四種類型。
趨勢性
某個變量隨著時間進展或自變量變化,呈現一種比較緩慢而長期的持續上升、下降、停留的同性質變動趨向,但變動幅度可能不相等。
季節性
某因素由于外部影響隨著自然季節的交替出現高峰與低谷的規律。
隨機性
個別為隨機變動,整體呈統計規律。
綜合性
實際變化情況是幾種變動的疊加或組合。預測時設法過濾除去不規則變動,突出反映趨勢性和周期性變動。
查看時間序列時首先要考慮的重要特征是否存在趨勢,意味著平均而言,測量值會隨著時間的推移而增加(或減少)?
是否存在季節性,這意味著與日歷時間(例如季節、季度、月份、星期幾等)相關的高點和低點有規律地重復模式?
有異常值嗎?在回歸中,離群值離你的線很遠。對于時間序列數據,您的異常值與其他數據相距甚遠。
是否存在與季節性因素無關的長期周期或時期?
隨著時間的推移是否存在恒定的方差,或者方差是非常量的?
序列水平或方差是否有任何突然變化?
趨勢性通常,時間序列中不具有周期性的系統變化稱為趨勢。趨勢是序列隨時間的持續增加或減少。從時間序列數據集中識別、建模甚至刪除趨勢信息可能會帶來好處。
趨勢類型有各種各樣的趨勢,通常分為:
確定性趨勢:這些是持續增加或減少的趨勢。
隨機性趨勢:這些趨勢會不一致地增加和減少。
一般來說,確定性趨勢更容易識別和刪除。
根據觀察范圍來分類趨勢:
全局趨勢:這些趨勢適用于整個時間序列。
本地趨勢:這些趨勢適用于時間序列的部分或子序列。
一般來說,全局趨勢更容易識別和應對。
識別趨勢可以繪制時間序列數據以查看趨勢是否明顯。
而在實踐中,識別時間序列中的趨勢可能是一個主觀過程。因此從時間序列中提取或刪除它可能同樣具有主觀性。
創建數據的線圖并檢查圖中的明顯趨勢。
在圖中添加線性和非線性趨勢線,看看趨勢是否明顯。
刪除趨勢具有趨勢的時間序列稱為非平穩的。可以對識別的趨勢進行建模。建模后,可以將其從時間序列數據集中刪除。這稱為去趨勢時間序列。
如果數據集沒有趨勢或我們成功地移除了趨勢,則稱該數據集是趨勢平穩的。
在機器學習中使用時間序列趨勢從機器學習的角度來看,數據的趨勢代表著兩個機會:
刪除信息:刪除扭曲輸入和輸出變量之間關系的系統信息。
添加信息:添加系統信息以改善輸入和輸出變量之間的關系。
具體來說,作為數據準備和清洗練習,可以從時間序列數據(以及未來的數據)中刪除趨勢。這在使用統計方法進行時間序列預測時很常見,但在使用機器學習模型時并不總是能改善結果。
季節性季節性被定義為周期性的波動,季節性變化或季節性是隨著時間有規律地重復的循環。
許多時間序列顯示季節性。例如,零售額往往在春季期間達到頂峰,然后在假期過后下降。因此,零售銷售的時間序列通常會顯示 1月至 3月的銷售額增加,而 4 月和 5 月的銷售額下降。季節性在經濟時間序列中很常見,它在工程和科學數據中不太常見。
時間序列中的周期結構可能是季節性的,也可能不是。如果它始終以相同的頻率重復,則是季節性的,否則就不是季節性的,稱為循環。
季節性類型季節性有很多種。例如:時間、日、每周、每月、每年。因此,確定時間序列問題中是否存在季節性成分是主觀的。
確定是否存在季節性因素的最簡單方法是繪制和查看數據,可能以不同的比例并添加趨勢線。
去除季節性一旦確定了季節性,就可以對其進行建模。季節性模型可以從時間序列中刪除。此過程稱為季節性調整[8]或去季節性[9]化。
去除了季節性成分的時間序列稱為季節性平穩。具有明顯季節性成分的時間序列被稱為非平穩的。
在時間序列分析領域,有一些復雜的方法可以從時間序列中研究和提取季節性。
機器學習中作用了解時間序列中的季節性成分可以提高機器學習建模的性能。
這可以通過兩種主要方式發生:
更清晰的信號:從時間序列中識別和去除季節性成分可以使輸入和輸出變量之間的關系更清晰。
更多信息:關于時間序列季節性分量的附加信息可以提供新信息以提高模型性能。
這兩種方法都可能對項目有用。并在數據清洗和準備期間就需要建模季節性并將其從時間序列中刪除。
在特征提取和特征工程期間,可能會提取季節性信息并將其作為輸入特征。
其他離群值:離群值離標準數據方差很遠。
長期循環:獨立于季節性因素,數據可能顯示一個長期周期,比如持續超過一年的經濟衰退。
恒定方差:隨著時間的推移,一些數據顯示出不斷的波動,比如每天和晚上的能源使用量。
突變:數據可能顯示出突變,可能需要進一步分析。例如,由于COVID而突然關閉的企業導致了數據的變化。
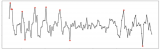
以下是時間序列樣本圖[11],顯示了玩家在過去幾年里每天花費在游戲中的貨幣。你能在這個數據中識別出上面列出的任何特征嗎?
時間序列預測方法基本規則通過人工經驗,挖掘時序數據的演化特征,找到時序變化的周期,從而預估時間序列的未來走勢。具體的觀察一個時間序列,當序列存在周期性時,提取時間序列的周期性特征進行預測。
傳統參數法傳統的參數預測方法可以分為兩種,
一種擬合標準時間序列的餐順方法,包括移動平均,指數平均等;
另一種是考慮多因素組合的參數方法,即 AR, MA, ARMA, ARIMA等模型。這類方法比較適用于小規模,單變量的預測。
時間序列分解一個時間序列往往是一下幾類變化形式的疊加或耦合
長期趨勢 (Secular trend, T)
長期趨勢指現象在較長時期內持續發展變化的一種趨向或狀態。
季節變動 (Seasonal Variation, S)
季節波動是由于季節的變化引起的現象發展水平的規則變動
循環波動 (Cyclical Variation, C)
循環波動指以若干年為期限,不具嚴格規則的周期性連續變動
不規則波動 (Irregular Variation, I)
不規則波動指由于眾多偶然因素對時間序列造成的影響
機器學習主要是構建樣本數據集,采用“時間特征”到“樣本值”的方式,通過有監督學習,學習特征與標簽之前的關聯關系,從而實現時間序列預測。
單步預測在時間序列預測中使用滯后的觀測值 ,作為輸入變量來預測當前的時間的觀測值
多步預測使用過去的觀測序列 來預測未來的觀測序列
多變量預測每個時間有多個觀測值:
通過不同的測量手段得到了多種觀測值,并且希望預測其中的一個或幾個值。
深度學習對于時間序列的分析,有許多方法可以進行處理,包括:循環神經網絡-LSTM模型 / 卷積神經網絡 / 基于注意力機制的模型(seq2seq)/。..
循環神經網絡循環神經網絡(RNN)框架及其變種(LSTM/GRU/。..)是為處理序列型而生的模型,天生的循環自回歸的結構是對時間序列的很好的表示
時間卷積網絡時間卷積網絡(TCN)是一種特殊的卷積神經網絡,針對一維空間做卷積,迭代多層捕捉長期關系。具體的,對于上一層t時刻的值,只依賴于下一層t時刻及其之前的值。
一個時間序列數據--電力使用數據開始創建一個時間序列模型,根據過去的使用情況來預測未來的電力使用量。
本例中的數據來自GEFCom2014預測競賽。由2012 - 2014年3年的小時電負荷和溫度值組成。
import os
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
data_dir = ‘。/data’
energy = pd.read_csv(‘。/energy.csv’)
energy.head()
可以看到有兩列表示date和load
load
2012-01-01 00002698.0
2012-01-01 01002558.0
2012-01-01 02002444.0
2012-01-01 03002402.0
2012-01-01 04002403.0
可視化energy.plot(y=‘load’, subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel(‘timestamp’, fontsize=12)
plt.ylabel(‘load’, fontsize=12)
plt.show()
現在,繪制2014年7月的第一周,將其作為energy的輸入,在[from date]: [to date] 模式中:
energy[‘2014-07-01’:‘2014-07-07’].plot(y=‘load’, subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel(‘timestamp’, fontsize=12)
plt.ylabel(‘load’, fontsize=12)
plt.show()
看看這些圖,看看你是否能確定上面列出的任何特征。通過可視化數據我們可以推測出什么?后面將介紹創建一個ARIMA模型來創建一些預測。
責任編輯:haq
-
數據
+關注
關注
8文章
6909瀏覽量
88849 -
時序設計
+關注
關注
0文章
21瀏覽量
43926
原文標題:一文解讀時間序列基本概念
文章出處:【微信號:DBDevs,微信公眾號:數據分析與開發】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何使用RNN進行時間序列預測
分享一些常見的電路
【「時間序列與機器學習」閱讀體驗】時間序列的信息提取
【《時間序列與機器學習》閱讀體驗】+ 時間序列的信息提取
【「時間序列與機器學習」閱讀體驗】+ 簡單建議
【《時間序列與機器學習》閱讀體驗】+ 了解時間序列
【「時間序列與機器學習」閱讀體驗】全書概覽與時間序列概述
深度學習中的時間序列分類方法
名單公布!【書籍評測活動NO.35】如何用「時間序列與機器學習」解鎖未來?
深度學習在時間序列預測的總結和未來方向分析

ICLR 2024高分投稿:用于一般時間序列分析的現代純卷積結構





 一些時間序列算法探索
一些時間序列算法探索












評論