之前經(jīng)常講涉及遞歸的算法題，我說過寫遞歸算法的一個技巧就是不要試圖跳進(jìn)遞歸細(xì)節(jié)，而是從遞歸框架上思考，從函數(shù)定義去理解遞歸函數(shù)到底該怎么實現(xiàn)。

而且我們前文學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)和算法的框架思維特別強調(diào)過，練習(xí)遞歸的框架思維最好方式就是從二叉樹相關(guān)題目開始刷，前文也有好幾篇手把手帶你刷二叉樹和二叉搜索樹的文章：

• 手把手帶你刷二叉樹（第一期）

• 手把手帶你刷二叉樹（第二期）

• 手把手帶你刷二叉樹（第三期）

• 手把手帶你刷二叉搜索樹（第一期）

• 手把手帶你刷二叉搜索樹（第二期）

• 手把手帶你刷二叉搜索樹（第三期）

之前的文章全部都是運用二叉樹的遞歸框架，幫你透過現(xiàn)象看本質(zhì)，明白二叉樹的各種題目本質(zhì)都是前中后序遍歷衍生出來的。

前文BFS 算法框架詳解是利用隊列迭代地遍歷二叉樹，不過使用的是層級遍歷，沒有遞歸遍歷中的前中后序之分。

由于現(xiàn)在面試越來越卷，很多讀者在后臺問我如何將前中后序的遞歸框架改寫成迭代形式。

首先我想說，遞歸改迭代從實用性的角度講是沒什么意義的，明明可以寫遞歸解法，為什么非要改成迭代的方式？

對于二叉樹來說，遞歸解法是最容易理解的，非要讓你改成迭代，頂多是考察你對遞歸和棧的理解程度，架不住大家問，那就總結(jié)一下吧。

我以前見過一些迭代實現(xiàn)二叉樹前中后序遍歷的代碼模板，比較短小，容易記，但通用性較差。

通用性較差的意思是說，模板只是針對「用迭代的方式返回二叉樹前/中/后序的遍歷結(jié)果」這個問題，函數(shù)簽名類似這樣，返回一個TreeNode列表：

Listtraverse(TreeNoderoot);

如果給一些稍微復(fù)雜的二叉樹問題，比如最近公共祖先，二叉搜索子樹的最大鍵值和，想把這些遞歸解法改成迭代，就無能為力了。

而我想要的是一個萬能的模板，可以把一切二叉樹遞歸算法都改成迭代。

換句話說，類似二叉樹的遞歸框架：

voidtraverse(TreeNoderoot){
if(root==null)return;
/*前序遍歷代碼位置*/
traverse(root.left);
/*中序遍歷代碼位置*/
traverse(root.right);
/*后序遍歷代碼位置*/
}

迭代框架也應(yīng)該有前中后序代碼的位置：

voidtraverse(TreeNoderoot){
while(...){
if(...){
/*前序遍歷代碼位置*/
}
if(...){
/*中序遍歷代碼位置*/
}
if(...){
/*后序遍歷代碼位置*/
}
}
}

我如果想把任何一道二叉樹遞歸解法改成迭代，直接把遞歸解法中前中后序?qū)?yīng)位置的代碼復(fù)制粘貼到迭代框架里，就可以直接運行，得到正確的結(jié)果。

理論上，所有遞歸算法都可以利用棧改成迭代的形式，因為計算機本質(zhì)上就是借助棧來迭代地執(zhí)行遞歸函數(shù)的。

所以本文就來利用「棧」模擬函數(shù)遞歸的過程，總結(jié)一套二叉樹通用迭代遍歷框架。

遞歸框架改為迭代

參加過我的二叉樹專項訓(xùn)練的讀者應(yīng)該知道，二叉樹的遞歸框架中，前中后序遍歷位置就是幾個特殊的時間點：

前序遍歷位置的代碼，會在剛遍歷到當(dāng)前節(jié)點root，遍歷root的左右子樹之前執(zhí)行；

中序遍歷位置的代碼，會在在遍歷完當(dāng)前節(jié)點root的左子樹，即將開始遍歷root的右子樹的時候執(zhí)行；

后序遍歷位置的代碼，會在遍歷完以當(dāng)前節(jié)點root為根的整棵子樹之后執(zhí)行。

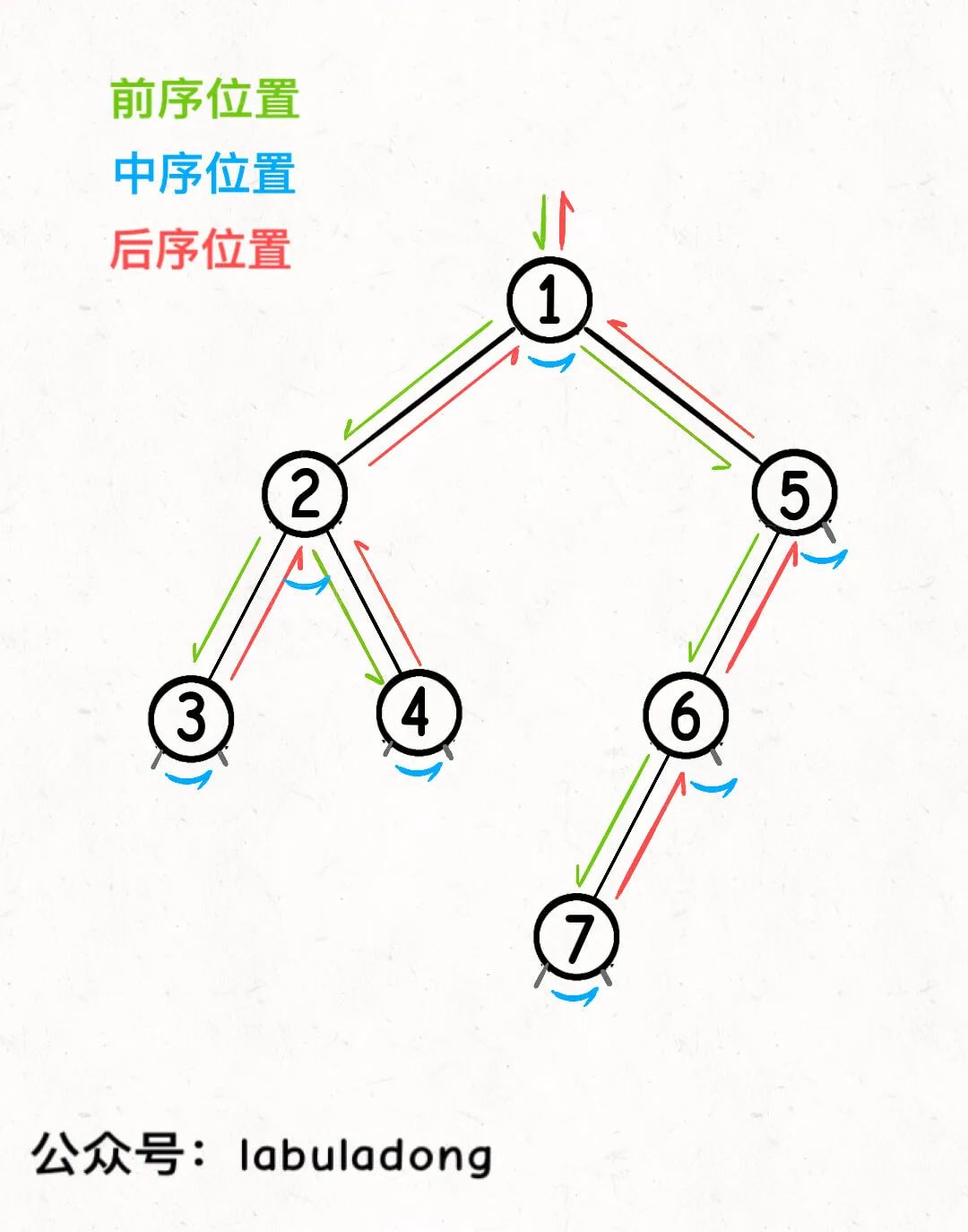
如果從遞歸代碼上來看，上述結(jié)論是很容易理解的：

voidtraverse(TreeNoderoot){
if(root==null)return;
/*前序遍歷代碼位置*/
traverse(root.left);
/*中序遍歷代碼位置*/
traverse(root.right);
/*后序遍歷代碼位置*/
}

不過，如果我們想將遞歸算法改為迭代算法，就不能從框架上理解算法的邏輯，而要深入細(xì)節(jié)，思考計算機是如何進(jìn)行遞歸的。

假設(shè)計算機運行函數(shù)A，就會把A放到調(diào)用棧里面，如果A又調(diào)用了函數(shù)B，則把B壓在A上面，如果B又調(diào)用了C，那就再把C壓到B上面……

當(dāng)C執(zhí)行結(jié)束后，C出棧，返回值傳給B，B執(zhí)行完后出棧，返回值傳給A，最后等A執(zhí)行完，返回結(jié)果并出棧，此時調(diào)用棧為空，整個函數(shù)調(diào)用鏈結(jié)束。

我們遞歸遍歷二叉樹的函數(shù)也是一樣的，當(dāng)函數(shù)被調(diào)用時，被壓入調(diào)用棧，當(dāng)函數(shù)結(jié)束時，從調(diào)用棧中彈出。

那么我們可以寫出下面這段代碼模擬遞歸調(diào)用的過程：

//模擬系統(tǒng)的函數(shù)調(diào)用棧
Stackstk=newStack<>();

voidtraverse(TreeNoderoot){
if(root==null)return;
//函數(shù)開始時壓入調(diào)用棧
stk.push(root);
traverse(root.left);
traverse(root.right);
//函數(shù)結(jié)束時離開調(diào)用棧
stk.pop();
}

如果在前序遍歷的位置入棧，后序遍歷的位置出棧，stk中的節(jié)點變化情況就反映了traverse函數(shù)的遞歸過程（綠色節(jié)點就是被壓入棧中的節(jié)點，灰色節(jié)點就是彈出棧的節(jié)點）：

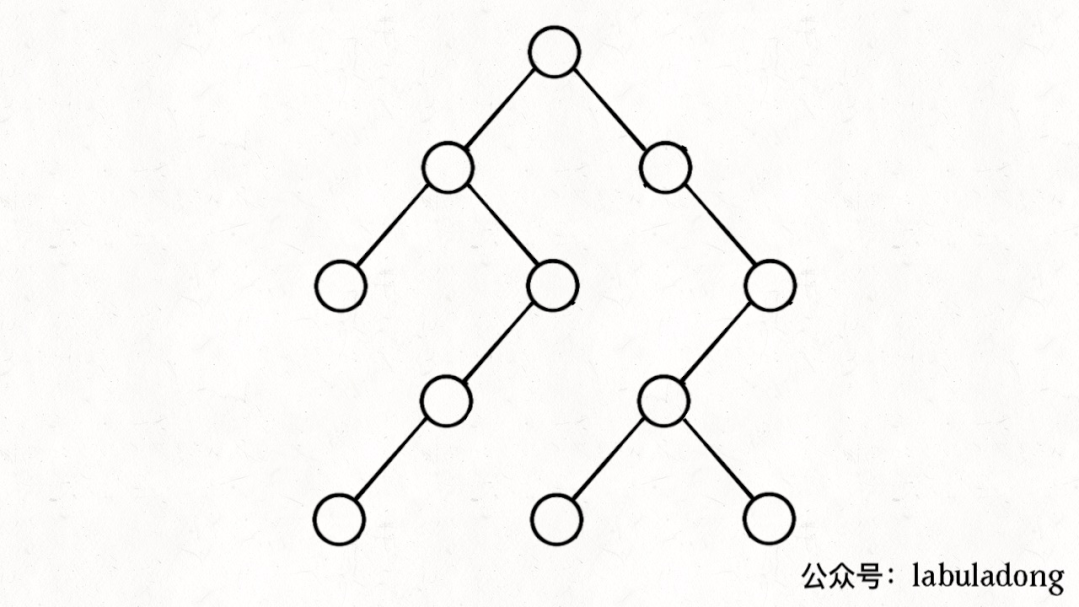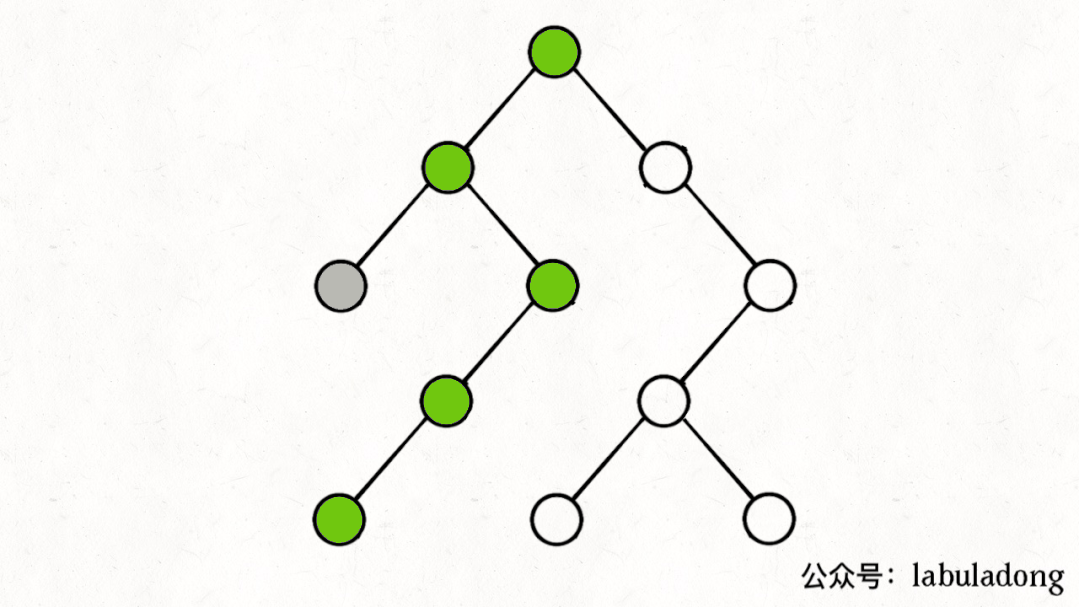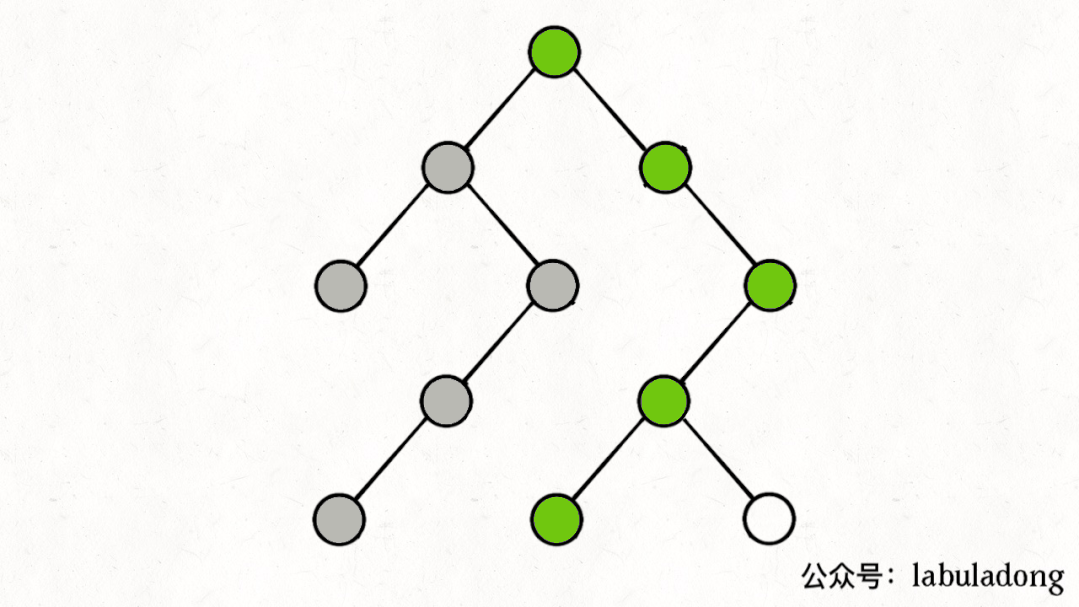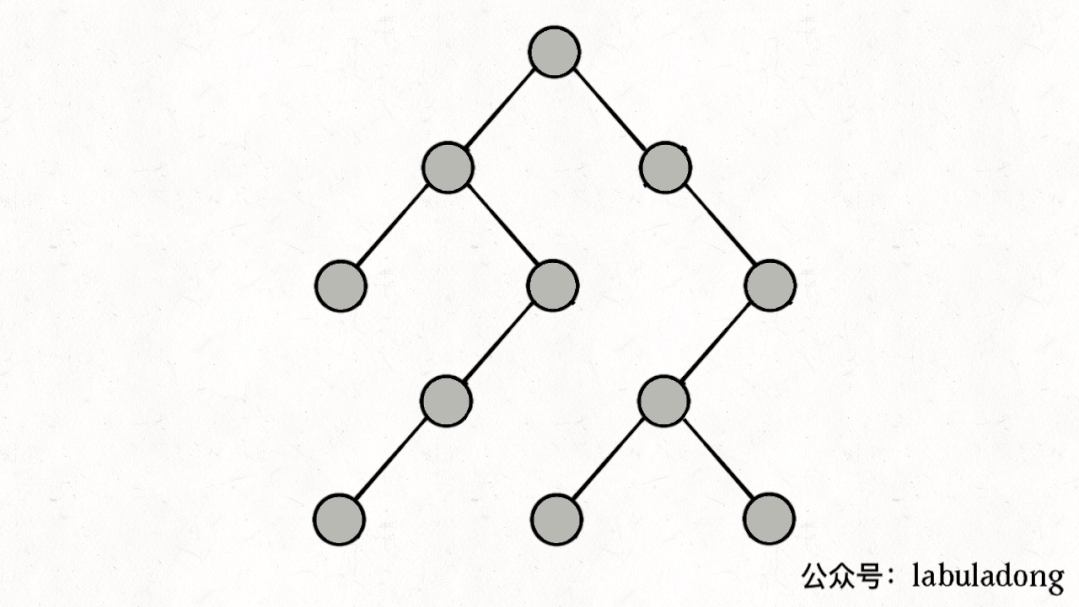
簡單說就是這樣一個流程：

1、拿到一個節(jié)點，就一路向左遍歷（因為traverse(root.left)排在前面），把路上的節(jié)點都壓到棧里。

2、往左走到頭之后就開始退棧，看看棧頂節(jié)點的右指針，非空的話就重復(fù)第 1 步。

寫成迭代代碼就是這樣：

privateStackstk=newStack<>();

publicListtraverse(TreeNoderoot){
pushLeftBranch(root);

while(!stk.isEmpty()){
TreeNodep=stk.pop();
pushLeftBranch(p.right);
}
}

//左側(cè)樹枝一擼到底，都放入棧中
privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
stk.push(p);
p=p.left;
}
}

上述代碼雖然已經(jīng)可以模擬出遞歸函數(shù)的運行過程，不過還沒有找到遞歸代碼中的前中后序代碼位置，所以需要進(jìn)一步修改。

迭代代碼框架

想在迭代代碼中體現(xiàn)前中后序遍歷，關(guān)鍵點在哪里？

當(dāng)我從棧中拿出一個節(jié)點p，我應(yīng)該想辦法搞清楚這個節(jié)點p左右子樹的遍歷情況。

如果p的左右子樹都沒有被遍歷，那么現(xiàn)在對p進(jìn)行操作就屬于前序遍歷代碼。

如果p的左子樹被遍歷過了，而右子樹沒有被遍歷過，那么現(xiàn)在對p進(jìn)行操作就屬于中序遍歷代碼。

如果p的左右子樹都被遍歷過了，那么現(xiàn)在對p進(jìn)行操作就屬于后序遍歷代碼。

上述邏輯寫成偽碼如下：

privateStackstk=newStack<>();

publicListtraverse(TreeNoderoot){
pushLeftBranch(root);

while(!stk.isEmpty()){
TreeNodep=stk.peek();

if(p的左子樹被遍歷完了){
/*******************/
/**中序遍歷代碼位置**/
/*******************/
//去遍歷p的右子樹
pushLeftBranch(p.right);
}

if(p的右子樹被遍歷完了){
/*******************/
/**后序遍歷代碼位置**/
/*******************/
//以p為根的樹遍歷完了，出棧
stk.pop();
}
}
}

privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
/*******************/
/**前序遍歷代碼位置**/
/*******************/
stk.push(p);
p=p.left;
}
}

有剛才的鋪墊，這段代碼應(yīng)該是不難理解的，關(guān)鍵是如何判斷p的左右子樹到底被遍歷過沒有呢？

其實很簡單，我們只需要維護(hù)一個visited指針，指向「上一次遍歷完成的根節(jié)點」，就可以判斷p的左右子樹遍歷情況了

下面是迭代遍歷二叉樹的完整代碼框架：

//模擬函數(shù)調(diào)用棧
privateStackstk=newStack<>();

//左側(cè)樹枝一擼到底
privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
/*******************/
/**前序遍歷代碼位置**/
/*******************/
stk.push(p);
p=p.left;
}
}

publicListtraverse(TreeNoderoot){
//指向上一次遍歷完的子樹根節(jié)點
TreeNodevisited=newTreeNode(-1);
//開始遍歷整棵樹
pushLeftBranch(root);

while(!stk.isEmpty()){
TreeNodep=stk.peek();

//p的左子樹被遍歷完了，且右子樹沒有被遍歷過
if((p.left==null||p.left==visited)
&&p.right!=visited){
/*******************/
/**中序遍歷代碼位置**/
/*******************/
//去遍歷p的右子樹
pushLeftBranch(p.right);
}
//p的右子樹被遍歷完了
if(p.right==null||p.right==visited){
/*******************/
/**后序遍歷代碼位置**/
/*******************/
//以p為根的子樹被遍歷完了，出棧
//visited指針指向p
visited=stk.pop();
}
}
}

代碼中最有技巧性的是這個visited指針，它記錄最近一次遍歷完的子樹根節(jié)點（最近一次pop出棧的節(jié)點），我們可以根據(jù)對比p的左右指針和visited是否相同來判斷節(jié)點p的左右子樹是否被遍歷過，進(jìn)而分離出前中后序的代碼位置。

PS：visited指針初始化指向一個新 new 出來的二叉樹節(jié)點，相當(dāng)于一個特殊值，目的是避免和輸入二叉樹中的節(jié)點重復(fù)。

只需把遞歸算法中的前中后序位置的代碼復(fù)制粘貼到上述框架的對應(yīng)位置，就可以把任意遞歸的二叉樹算法改寫成迭代形式了。

比如，讓你返回二叉樹后序遍歷的結(jié)果，你就可以這樣寫：

privateStackstk=newStack<>();

publicListpostorderTraversal(TreeNoderoot){
//記錄后序遍歷的結(jié)果
Listpostorder=newArrayList<>();
TreeNodevisited=newTreeNode(-1);

pushLeftBranch(root);
while(!stk.isEmpty()){
TreeNodep=stk.peek();

if((p.left==null||p.left==visited)
&&p.right!=visited){
pushLeftBranch(p.right);
}

if(p.right==null||p.right==visited){
//后序遍歷代碼位置
postorder.add(p.val);
visited=stk.pop();
}
}

returnpostorder;
}

privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
stk.push(p);
p=p.left;
}
}

當(dāng)然，任何一個二叉樹的算法，如果你想把遞歸改成迭代，都可以套用這個框架，只要把遞歸的前中后序位置的代碼對應(yīng)過來就行了。

迭代解法到這里就搞定了，不過我還是想強調(diào)，除了 BFS 層級遍歷之外，二叉樹的題目還是用遞歸的方式來做，因為遞歸是最符合二叉樹結(jié)構(gòu)特點的。

說到底，這個迭代解法就是在用棧模擬遞歸調(diào)用，所以對照著遞歸解法，應(yīng)該不難理解和記憶。