雙指針技巧在處理數組和鏈表相關問題時經常用到，主要分為兩類：左右指針和快慢指針。

所謂左右指針，就是兩個指針相向而行或者相背而行；而所謂快慢指針，就是兩個指針同向而行，一快一慢。

對于單鏈表來說，大部分技巧都屬于快慢指針，前文 單鏈表的六大解題套路 都涵蓋了，比如鏈表環判斷，倒數第K個鏈表節點等問題，它們都是通過一個fast快指針和一個slow慢指針配合完成任務。

在數組中并沒有真正意義上的指針，但我們可以把索引當做數組中的指針，這樣也可以在數組中施展雙指針技巧，本文主要講數組相關的雙指針算法。

一、快慢指針技巧

數組問題中比較常見且難度不高的的快慢指針技巧，是讓你原地修改數組。

比如說看下力扣第 26 題「刪除有序數組中的重復項」，讓你在有序數組去重：

函數簽名如下：

intremoveDuplicates(int[]nums);

簡單解釋一下什么是原地修改：

如果不是原地修改的話，我們直接 new 一個int[]數組，把去重之后的元素放進這個新數組中，然后返回這個新數組即可。

但是現在題目讓你原地刪除，不允許 new 新數組，只能在原數組上操作，然后返回一個長度，這樣就可以通過返回的長度和原始數組得到我們去重后的元素有哪些了。

由于數組已經排序，所以重復的元素一定連在一起，找出它們并不難。但如果毎找到一個重復元素就立即原地刪除它，由于數組中刪除元素涉及數據搬移，整個時間復雜度是會達到O(N^2)。

高效解決這道題就要用到快慢指針技巧：

我們讓慢指針slow走在后面，快指針fast走在前面探路，找到一個不重復的元素就賦值給slow并讓slow前進一步。

這樣，就保證了nums[0..slow]都是無重復的元素，當fast指針遍歷完整個數組nums后，nums[0..slow]就是整個數組去重之后的結果。

看代碼：

intremoveDuplicates(int[]nums){
if(nums.length==0){
return0;
}
intslow=0,fast=0;
while(fastif(nums[fast]!=nums[slow]){
slow++;
//維護nums[0..slow]無重復
nums[slow]=nums[fast];
}
fast++;
}
//數組長度為索引+1
returnslow+1;
}

算法執行的過程如下 GIF 圖：

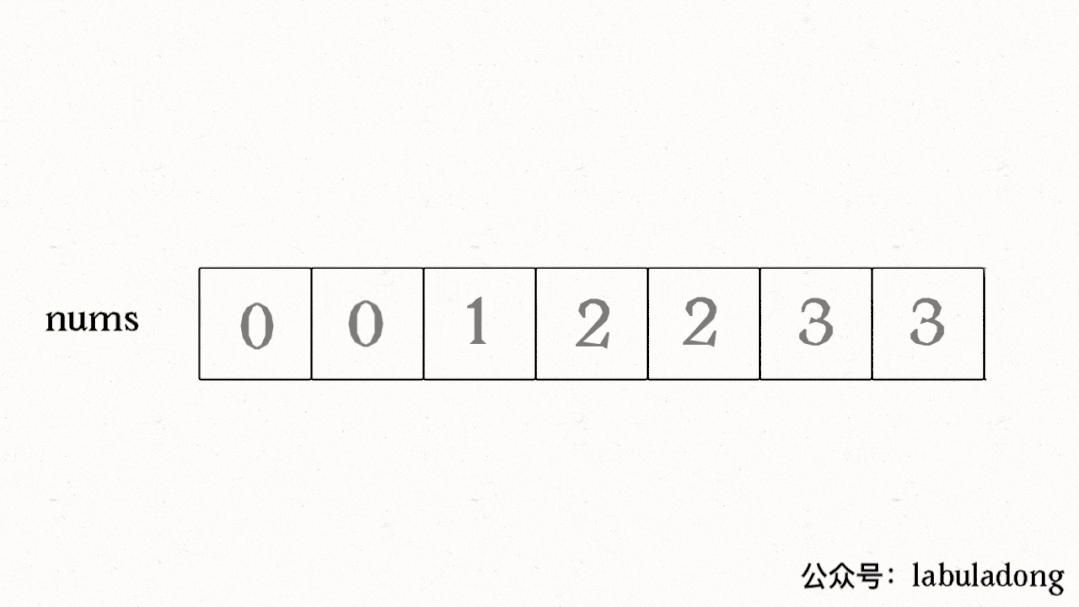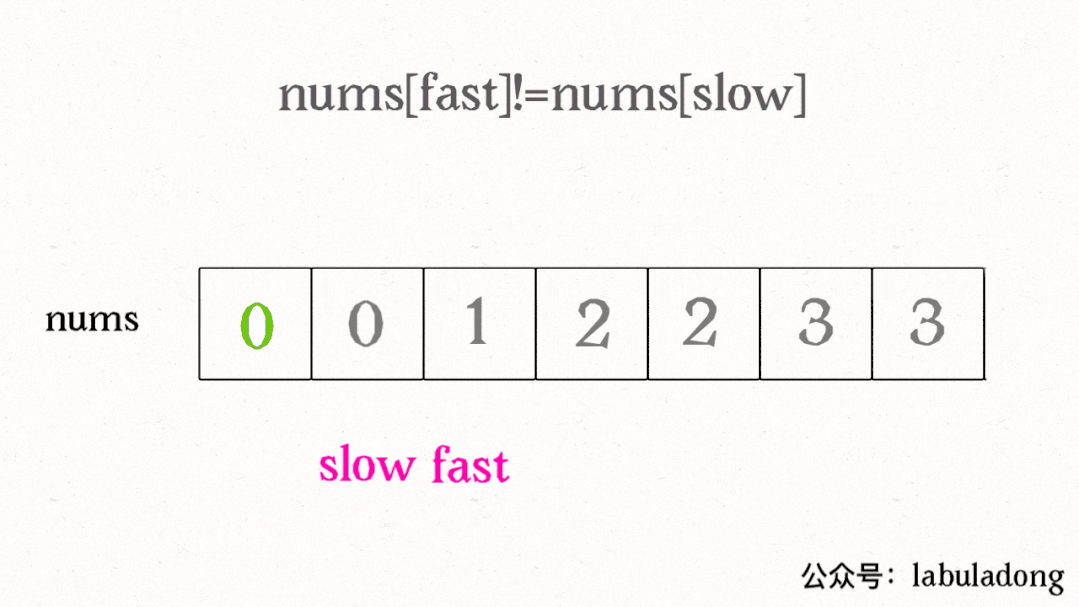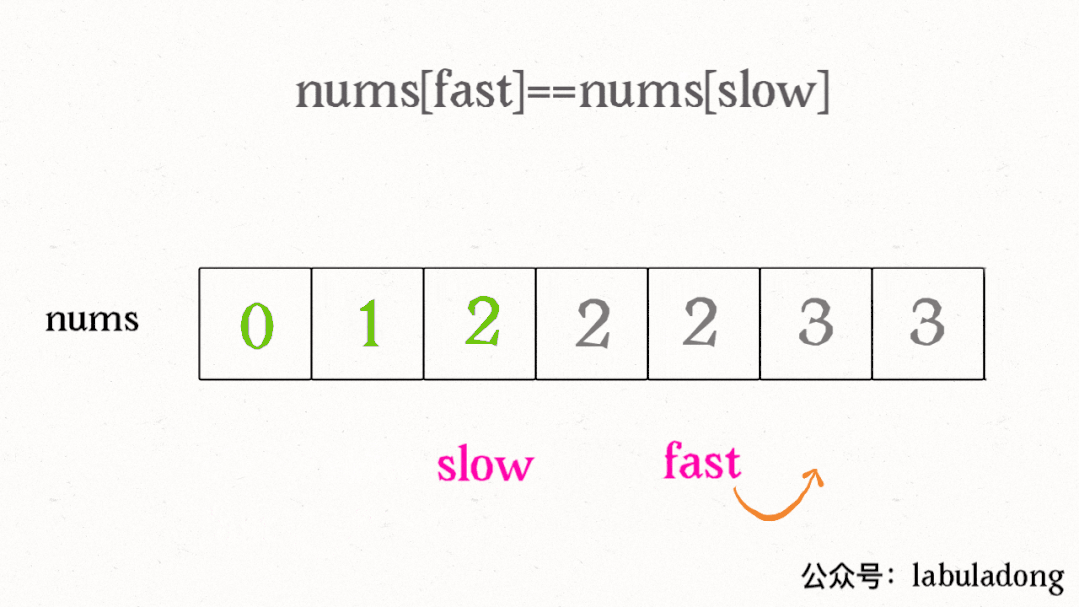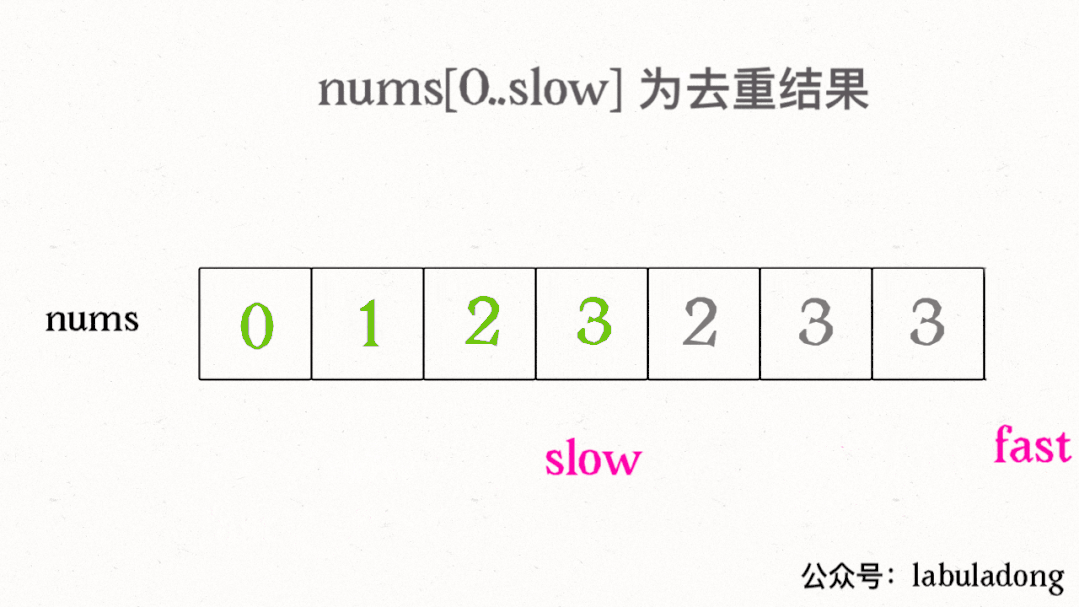
再簡單擴展一下，看看力扣第 83 題「刪除排序鏈表中的重復元素」，如果給你一個有序的單鏈表，如何去重呢？

其實和數組去重是一模一樣的，唯一的區別是把數組賦值操作變成操作指針而已，你對照著之前的代碼來看：

ListNodedeleteDuplicates(ListNodehead){
if(head==null)returnnull;
ListNodeslow=head,fast=head;
while(fast!=null){
if(fast.val!=slow.val){
//nums[slow]=nums[fast];
slow.next=fast;
//slow++;
slow=slow.next;
}
//fast++
fast=fast.next;
}
//斷開與后面重復元素的連接
slow.next=null;
returnhead;
}

算法執行的過程請看下面這個 GIF：

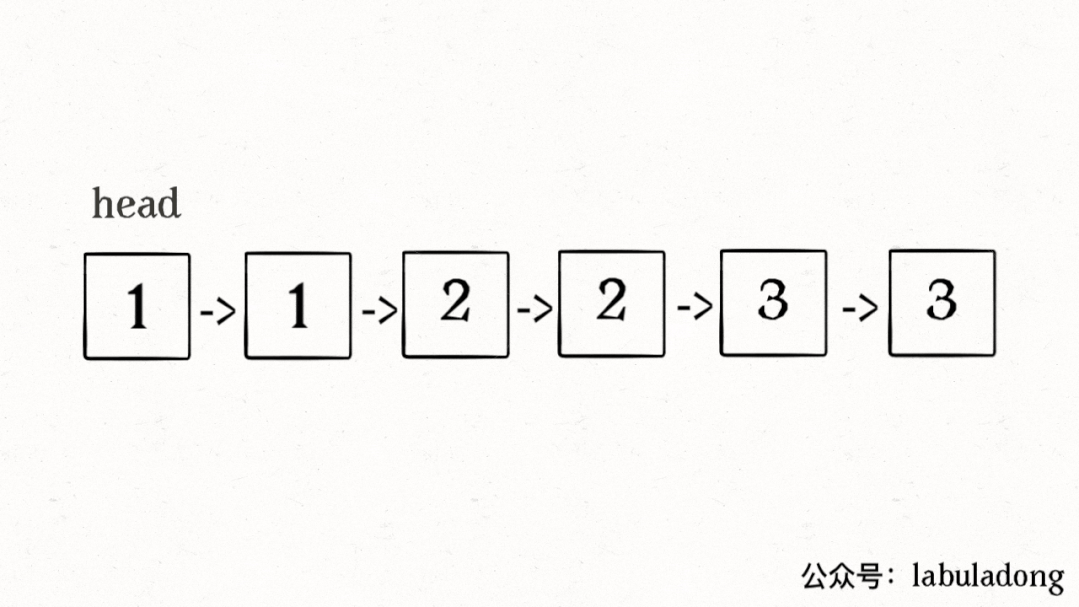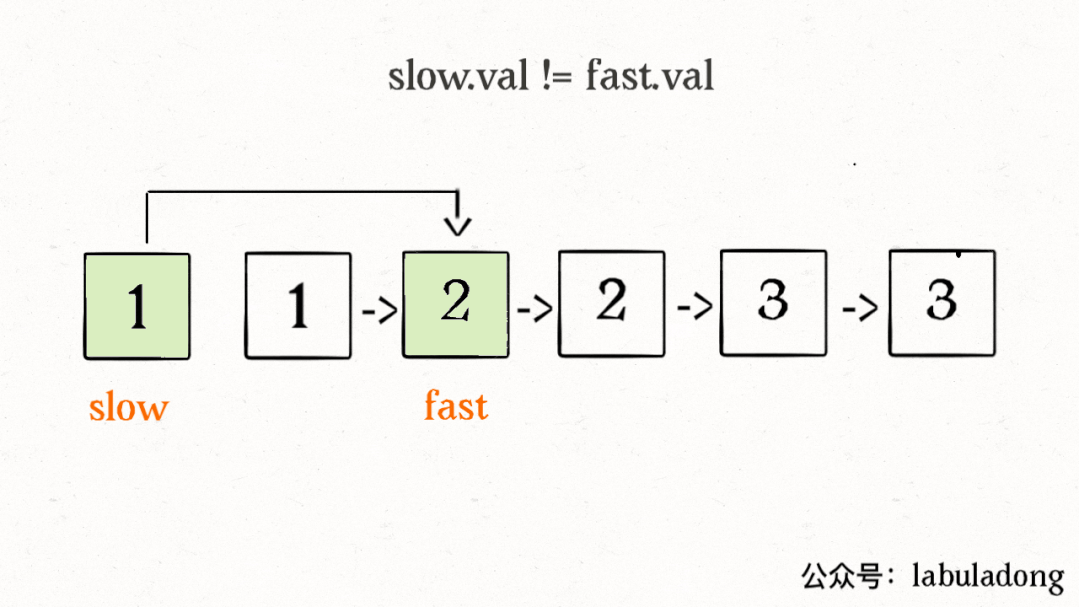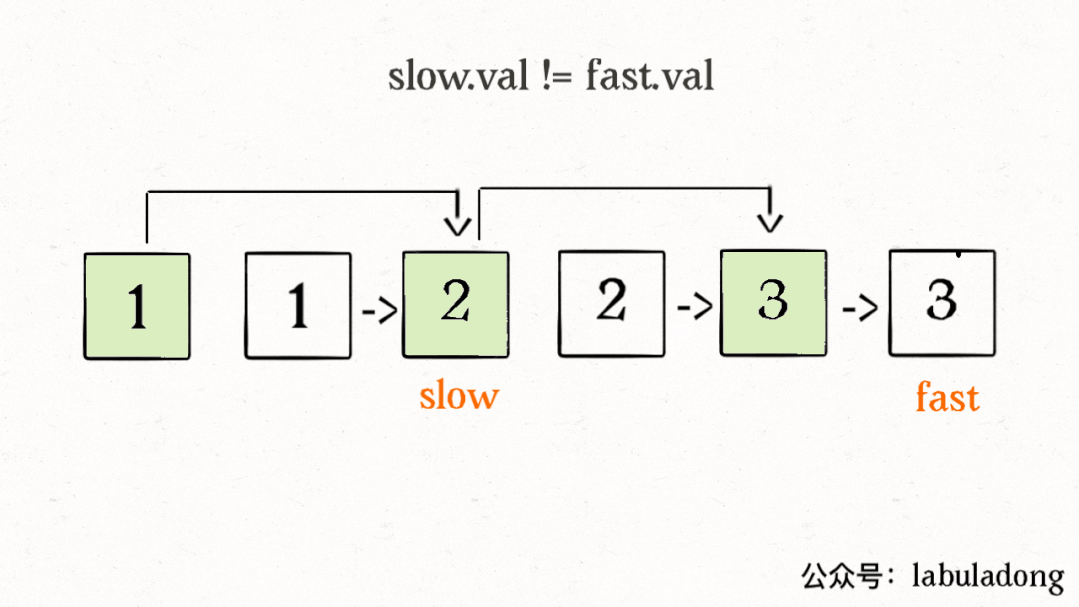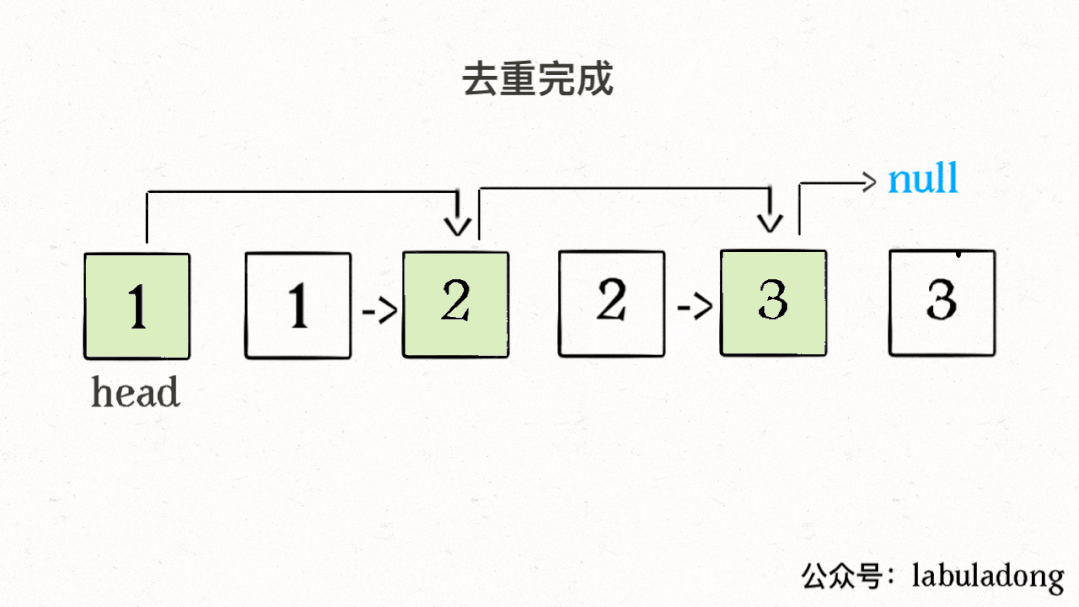
這里可能有讀者會問，鏈表中那些重復的元素并沒有被刪掉，就讓這些節點在鏈表上掛著，合適嗎？

這就要探討不同語言的特性了，像 Java/Python 這類帶有垃圾回收的語言，可以幫我們自動找到并回收這些「懸空」的鏈表節點的內存，而像 C++ 這類語言沒有自動垃圾回收的機制，確實需要我們編寫代碼時手動釋放掉這些節點的內存。

不過話說回來，就算法思維的培養來說，我們只需要知道這種快慢指針技巧即可。

除了讓你在有序數組/鏈表中去重，題目還可能讓你對數組中的某些元素進行「原地刪除」。

比如力扣第 27 題「移除元素」，看下題目：

函數簽名如下：

intremoveElement(int[]nums,intval);

題目要求我們把nums中所有值為val的元素原地刪除，依然需要使用快慢指針技巧：

如果fast遇到值為val的元素，則直接跳過，否則就賦值給slow指針，并讓slow前進一步。

這和前面說到的數組去重問題解法思路是完全一樣的，就不畫 GIF 了，直接看代碼：

intremoveElement(int[]nums,intval){
intfast=0,slow=0;
while(fastif(nums[fast]!=val){
nums[slow]=nums[fast];
slow++;
}
fast++;
}
returnslow;
}

注意這里和有序數組去重的解法有一個細節差異，我們這里是先給nums[slow]賦值然后再給slow++，這樣可以保證nums[0..slow-1]是不包含值為val的元素的，最后的結果數組長度就是slow。

實現了這個removeElement函數，接下來看看力扣第 283 題「移動零」：

給你輸入一個數組nums，請你原地修改，將數組中的所有值為 0 的元素移到數組末尾，函數簽名如下：

voidmoveZeroes(int[]nums);

比如說給你輸入nums = [0,1,4,0,2]，你的算法沒有返回值，但是會把nums數組原地修改成[1,4,2,0,0]。

結合之前說到的幾個題目，你是否有已經有了答案呢？

題目讓我們將所有 0 移到最后，其實就相當于移除nums中的所有 0，然后再把后面的元素都賦值為 0 即可。

所以我們可以復用上一題的removeElement函數：

voidmoveZeroes(int[]nums){
//去除nums中的所有0，返回不含0的數組長度
intp=removeElement(nums,0);
//將nums[p..]的元素賦值為0
for(;p0;
}
}

//見上文代碼實現
intremoveElement(int[]nums,intval);

到這里，原地修改數組的這些題目就已經差不多了。數組中另一大類快慢指針的題目就是「滑動窗口算法」。

我在另一篇文章 滑動窗口算法核心框架詳解 給出了滑動窗口的代碼框架：

/*滑動窗口算法框架*/
voidslidingWindow(strings,stringt){
unordered_map<char,int>need,window;
for(charc:t)need[c]++;

intleft=0,right=0;
intvalid=0;
while(rightcharc=s[right];
//右移（增大）窗口
right++;
//進行窗口內數據的一系列更新

while(windowneedsshrink){
chard=s[left];
//左移（縮小）窗口
left++;
//進行窗口內數據的一系列更新
}
}
}

具體的題目本文就不重復了，這里只強調滑動窗口算法的快慢指針特性：

left指針在后，right指針在前，兩個指針中間的部分就是「窗口」，算法通過擴大和縮小「窗口」來解決某些問題。

二、左右指針的常用算法

1、二分查找

我在另一篇文章 二分查找框架詳解 中有詳細探討二分搜索代碼的細節問題，這里只寫最簡單的二分算法，旨在突出它的雙指針特性：

intbinarySearch(int[]nums,inttarget){
//一左一右兩個指針相向而行
intleft=0,right=nums.length-1;
while(left<=?right)?{
????????intmid=(right+left)/2;
if(nums[mid]==target)
returnmid;
elseif(nums[mid]1;
elseif(nums[mid]>target)
right=mid-1;
}
return-1;
}

2、兩數之和

看下力扣第 167 題「兩數之和 II」：

只要數組有序，就應該想到雙指針技巧。這道題的解法有點類似二分查找，通過調節left和right就可以調整sum的大小：

int[]twoSum(int[]nums,inttarget){
//一左一右兩個指針相向而行
intleft=0,right=nums.length-1;
while(leftintsum=nums[left]+nums[right];
if(sum==target){
//題目要求的索引是從1開始的
returnnewint[]{left+1,right+1};
}elseif(sum//讓sum大一點
}elseif(sum>target){
right--;//讓sum小一點
}
}
returnnewint[]{-1,-1};
}

我在另一篇文章 一個函數秒殺所有 nSum 問題 中也運用類似的左右指針技巧給出了nSum問題的一種通用思路，這里就不做贅述了。

3、反轉數組

一般編程語言都會提供reverse函數，其實這個函數的原理非常簡單，力扣第 344 題「反轉字符串」就是類似的需求，讓你反轉一個char[]類型的字符數組，我們直接看代碼吧：

voidreverseString(char[]s){
//一左一右兩個指針相向而行
intleft=0,right=s.length-1;
while(left//交換s[left]和s[right]
chartemp=s[left];
s[left]=s[right];
s[right]=temp;
left++;
right--;
}
}

4、回文串判斷

首先明確一下，回文串就是正著讀和反著讀都一樣的字符串。

比如說字符串aba和abba都是回文串，因為它們對稱，反過來還是和本身一樣；反之，字符串abac就不是回文串。

現在你應該能感覺到回文串問題和左右指針肯定有密切的聯系，比如讓你判斷一個字符串是不是回文串，你可以寫出下面這段代碼：

booleanisPalindrome(Strings){
//一左一右兩個指針相向而行
intleft=0,right=s.length()-1;
while(leftif(s.charAt(left)!=s.charAt(right)){
returnfalse;
}
left++;
right--;
}
returntrue;
}

那接下來我提升一點難度，給你一個字符串，讓你用雙指針技巧從中找出最長的回文串，你會做嗎？

這就是力扣第 5 題「最長回文子串」：

函數簽名如下：

StringlongestPalindrome(Strings);

找回文串的難點在于，回文串的的長度可能是奇數也可能是偶數，解決該問題的核心是從中心向兩端擴散的雙指針技巧。

如果回文串的長度為奇數，則它有一個中心字符；如果回文串的長度為偶數，則可以認為它有兩個中心字符。所以我們可以先實現這樣一個函數：

//在s中尋找以s[l]和s[r]為中心的最長回文串
Stringpalindrome(Strings,intl,intr){
//防止索引越界
while(l>=0&&r//雙指針，向兩邊展開
l--;r++;
}
//返回以s[l]和s[r]為中心的最長回文串
returns.substring(l+1,r);
}

這樣，如果輸入相同的l和r，就相當于尋找長度為奇數的回文串，如果輸入相鄰的l和r，則相當于尋找長度為偶數的回文串。

那么回到最長回文串的問題，解法的大致思路就是：

for0<=?i?1]為中心的回文串
更新答案

翻譯成代碼，就可以解決最長回文子串這個問題：

StringlongestPalindrome(Strings){
Stringres="";
for(inti=0;i//以s[i]為中心的最長回文子串
Strings1=palindrome(s,i,i);
//以s[i]和s[i+1]為中心的最長回文子串
Strings2=palindrome(s,i,i+1);
//res=longest(res,s1,s2)
res=res.length()>s1.length()?res:s1;
res=res.length()>s2.length()?res:s2;
}
returnres;
}

你應該能發現最長回文子串使用的左右指針和之前題目的左右指針有一些不同：之前的左右指針都是從兩端向中間相向而行，而回文子串問題則是讓左右指針從中心向兩端擴展。

不過這種情況也就回文串這類問題會遇到，所以我也把它歸為左右指針了。

到這里，數組相關的雙指針技巧就全部講完了，希望大家以后遇到類似的算法問題時能夠活學活用，舉一反三。

--- EOF ---

審核編輯 ：李倩