這篇文章是我將為 Parallel Forall 撰寫的系列文章中的第一篇，該系列文章旨在為 深度學習 提供一個直觀而溫和的介紹。它涵蓋了最重要的深度學習概念，旨在提供對每個概念的理解，而不是其數學和理論細節。雖然數學術語有時是必要的，并且可以進一步理解，但這些文章盡可能使用類比和圖像來提供易于理解的信息，包括對深度學習領域的直觀概述。

我以術語表的風格編寫了這個系列，因此它也可以作為深入學習概念的參考。

第一部分主要介紹深度學習的主要概念。 第二部分 提供歷史背景，并深入研究用于深度學習培訓的培訓程序、算法和實用技巧。 第三部分 涵蓋了序列學習，包括遞歸神經網絡、 LSTMs 和用于神經機器翻譯的編解碼器系統。 第四部分 涵蓋強化學習。

核心概念

機器學習

在機器學習中，我們（ 1 ）獲取一些數據，（ 2 ）根據這些數據訓練一個模型，（ 3 ）使用訓練的模型對新數據進行預測。 訓練 一個模型的過程可以看作是一個學習過程，在這個過程中，模型一步一步地暴露在新的、不熟悉的數據中。在每一步中，模型都會做出預測，并得到關于其生成的預測有多精確的反饋。這種反饋是根據某種度量（例如距正確解的距離）提供的誤差，用于校正預測中的誤差。

學習過程通常是參數空間中來回的游戲：如果你調整模型的一個參數以獲得正確的預測，那么模型可能會因此得到之前正確的預測錯誤。訓練一個具有良好預測性能的模型可能需要多次迭代。這個迭代的預測和調整過程一直持續到模型的預測不再改善為止。

特征工程

特征工程是從數據中提取有用模式的藝術，這將使 機器學習 模型更容易區分類。例如，你可以用綠色像素和藍色像素的數量作為一個指標，來判斷某張圖片中是陸地動物還是水生動物。這個特性對機器學習模型很有幫助，因為它限制了要進行良好分類所需考慮的類的數量。

當你想在大多數預測任務中獲得好的結果時，特征工程是最重要的技能。然而，由于不同的數據集和不同的數據類型需要不同的特征工程方法，因此很難學習和掌握。藝術不僅僅是一門粗糙的科學，更是一門科學。可用于一個數據集的特征通常不適用于其他數據集（例如，下一個圖像數據集僅包含陸地動物）。特征工程的難度和所涉及的工作量是尋找能夠學習特征的算法的主要原因，即自動生成特征的算法。

雖然許多任務可以通過特征學習（如對象和語音識別）實現自動化，但特征工程仍然是 在困難的任務中最有效的方法 （就像 Kaggle 機器學習競賽中的大多數任務一樣）。

特征學習

特征學習算法可以找到對區分類很重要的共同模式，并自動提取它們以用于分類或回歸過程。特征學習可以被認為是由算法自動完成的 特征工程 。在深度學習中，卷積層特別擅長于在圖像中找到好的特征到下一層，從而形成一個非線性特征的層次結構，這些特征的復雜性不斷增加（例如，斑點、邊緣 – 》鼻子、眼睛、臉頰 – 》面部）。最后一層使用所有這些生成的特征進行分類或回歸（卷積網絡中的最后一層本質上是多項式 邏輯回歸 ）。

圖 1 ：從深度學習算法中學習的層次特征。每個特征都可以看作是一個過濾器，它過濾輸入圖像的特征（鼻子）。如果找到了特征，負責的單元會產生大量的激活，這些激活可以被后面的分類器階段提取出來，作為類存在的良好指示器。圖片由 Honglak Lee 和同事（ 2011 年）發表在“用卷積深信念網絡進行分層表征的無監督學習”。

圖 1 顯示了由深度學習算法生成的特性，該算法可以生成易于解釋的特性。這很不尋常。特征通常很難解釋，尤其是在像 循環神經網絡 和 LSTM 這樣的深層網絡或非常深的卷積網絡中。

深度學習

在分層 特征學習 中，我們提取多層非線性特征并將其傳遞給一個分類器，該分類器將所有特征組合起來進行預測。我們感興趣的是將這些非常深層次的非線性特征疊加起來，因為我們無法從幾層中學習復雜的特性。從數學上可以看出，對于圖像來說，單個圖層的最佳特征是邊緣和斑點，因為它們包含了我們可以從單個非線性變換中提取的大部分信息。為了生成包含更多信息的特征，我們不能直接對輸入進行操作，但是我們需要再次轉換我們的第一個特征（邊緣和斑點），以獲得包含更多信息的更復雜的特征，以區分類。

有研究表明，人腦做的是完全相同的事情：在視覺皮層接收信息的第一層神經元對特定的邊緣和斑點很敏感，而視覺管道下游的大腦區域則對更復雜的結構（如臉部）敏感。

雖然分層特征學習在領域深度學習存在之前就被使用了，但是這些架構面臨著諸如消失 梯度 問題，其中梯度變得太小，無法為非常深的層提供學習信號，因此，與淺層學習算法（如支持向量機）相比，這些體系結構的性能較差。

“深度學習”一詞源于新的方法和策略，這些方法和策略旨在通過克服梯度消失的問題來生成這些深層的非線性特征層次，以便我們可以訓練具有數十層非線性層次特征的體系結構。在 2010 年早期，有研究表明，結合 GPUs 和 激活函數 提供更好的梯度流，足以在沒有重大困難的情況下訓練深層結構。從這里開始，人們對深入學習的興趣與日俱增。

深度學習不僅與學習深度非線性層次特征有關，還與學習檢測序列數據中非常長的非線性時間依賴性有關。雖然大多數其他處理順序數據的算法只有最后 10 個時間步的內存， 長短時記憶 循環神經網絡 （由 Sepp Hochreiter 和 J ü rgen-Schmidhuber 在 1997 年發明）允許網絡收集過去幾百個時間步的活動，從而做出準確的預測。雖然 LSTM 網絡在過去 10 年中大多被忽視，但自 2013 年以來， LSTM 網絡的使用量迅速增長，與卷積網絡一起構成了深度學習的兩大成功案例之一。

基本概念

對數幾率回歸

回歸分析估計統計輸入變量之間的關系，以便預測結果變量。 Logistic 回歸是一種回歸模型，它使用輸入變量來預測一個分類結果變量，該變量可以采用一組有限的類值，例如“ cancer ”/“ no cancer ”，或者圖像類別，如“ bird ”/“ car ”/“ dog ”/“ cat ”/“ horse ”。

Logistic 回歸將 Logistic sigmoid 函數（見圖 2 ）應用于加權輸入值，以預測輸入數據屬于哪兩類（或者在多項式 Logistic 回歸的情況下，是多個類別中的哪一個）。

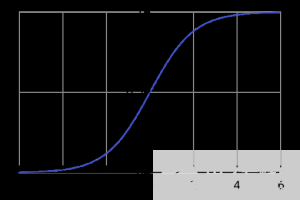
圖 2 ： logistic sigmoid 函數$ latex f （ x ）=\ frac { 1 }{ 1 + e ^{ -x }}}$。 圖像源

Logistic 回歸類似于非線性 感知器 或沒有隱藏層的神經網絡。與其他基本模型的主要區別在于，如果輸入變量的某些統計特性成立， logistic 回歸易于解釋且可靠。如果這些統計特性成立，我們可以用很少的輸入數據生成一個非常可靠的模型。這使得 logistic 回歸對于缺乏數據的領域很有價值，比如醫學和社會科學領域， logistic 回歸用于分析和解釋實驗結果。因為它簡單、快速，所以它也適用于非常大的數據集。

在深度學習中，用于分類的神經網絡的最后一層通常可以解釋為邏輯回歸。在這種情況下，我們可以將深度學習算法視為多個特征學習階段，然后將其特征傳遞到 logistic 回歸中，對輸入進行分類。

人工神經網絡

人工神經網絡（ 1 ）獲取一些輸入數據，（ 2 ）通過計算輸入的加權和來轉換這些輸入數據，（ 3 ）將一個非線性函數應用于此轉換以計算中間狀態。上面的三個步驟構成了所謂的 層 ，而轉換函數通常被稱為 單元 。通常稱為特征的中間狀態被用作另一層的輸入。

通過重復這些步驟，人工神經網絡學習多層非線性特征，然后將這些非線性特征組合到最后一層來創建預測。

神經網絡通過產生一個誤差信號來學習，該信號測量網絡的預測值與期望值之間的差異，然后使用該誤差信號來改變權重（或參數），從而使預測更加準確。

單位

單元通常指的是層中的 激活函數 ，通過該層，輸入通過非線性激活函數（例如通過 形函數 ）進行轉換。通常，一個單元有幾個傳入連接和幾個傳出連接。然而，單元也可以更復雜，比如 長短時記憶 單元，它有多個激活函數，與非線性激活函數有不同的連接布局，或者 maxout 單元，它通過一系列非線性轉換的輸入值計算最終輸出。 聯營 、 卷積 和其他輸入轉換函數通常不被稱為單元。

人工神經元

“人工神經元”或“神經元”這一術語與 單元 是一個等價的術語，但它意味著與神經生物學和人腦有著密切的聯系，而深度學習與大腦幾乎沒有任何關系（例如，現在人們認為生物神經元更類似于整個多層感知器，而不是神經網絡）。在上一次 艾冬 之后，人們鼓勵使用“神經元”這個詞來區分更成功的神經網絡與失敗和被遺棄的感知器。然而，自 2012 年后深度學***成功之后，媒體往往會拿起“神經元”一詞，試圖將深度學習解釋為人腦的模仿，這對深度學習領域的認知非常誤導，也有潛在的危險。現在不鼓勵使用“神經元”一詞，而應該使用更具描述性的術語“單位”。

激活函數

激活函數接受加權數據（輸入數據和權重之間的矩陣乘法）并輸出數據的非線性轉換。例如，$ latex output = max （ 0 ， weighted _ data ）$是 校正線性激活函數 （基本上將所有負值設置為零）。單元和激活函數之間的區別在于，單元可以更復雜，也就是說，一個單元可以有多個激活函數（例如 LSTM 單元）或稍微復雜一些的結構（例如 maxout 單元）。

線性激活函數和非線性激活函數之間的區別可以用一些加權值的關系來表示：想象四個點 A1 號 、 A2 、 地下一層 和 地下二層 。對 A1 號 / A2 和 地下一層 / 地下二層 彼此靠近，但 A1 號 與 地下一層 和 地下二層 相距較遠，反之亦然； A2 也是如此。

通過線性變換，對之間的關系 MIG ht 發生變化。例如 A1 號 和 A2 MIG ht 相距很遠，但這意味著 地下一層 和 地下二層 也相距很遠。兩對 MIG ht 之間的距離會縮小，但如果確實如此，那么 地下一層 和 地下二層 將同時接近 A1 號 和 A2 。我們可以應用許多線性變換，但是 A1 號 / A2 和 地下一層 / 地下二層 之間的關系總是相似的。

相反，通過非線性激活函數，我們可以增加 A1 號 和 A2 之間的距離，而我們 減少 可以增加 地下一層 和 地下二層 之間的距離。我們可以使 地下一層 靠近 A1 號 ，但 地下二層 遠離 A1 號 。通過應用非線性函數，我們在點之間創建新的關系。隨著每一個新的非線性變換，我們可以增加關系的復雜性。在深度學習中，使用非線性激活函數會為每一層創建越來越復雜的特征。

相反， 1000 層純線性變換的特征可以由一個單層再現（因為矩陣乘法鏈總是可以用一個矩陣乘法表示）。這就是為什么非線性激活函數在深度學習中如此重要。

層

層是深度學習的最高層次的構建塊。層是一個容器，它通常接收加權輸入，用一組非線性函數對其進行轉換，然后將這些值作為輸出傳遞到下一層。一個層通常是統一的，即它只包含一種類型的激活函數， 聯營 ， 卷積 等，因此可以很容易地與網絡的其他部分進行比較。網絡中的第一層和最后一層分別稱為輸入層和輸出層，中間的所有層稱為隱藏層。

卷積式深度學習

卷積

卷積是一種數學運算，它描述了如何混合兩個函數或信息的規則：（ 1 ）特征映射（或輸入數據）和（ 2 ）卷積核混合在一起形成（ 3 ）轉換后的特征映射。卷積通常被解釋為一種濾波器，在這種濾波器中，核對特征映射進行某種類型的信息過濾（例如，一個核 MIG ht 濾波器用于邊緣并丟棄其他信息）。

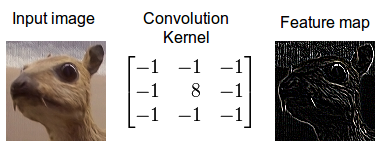
圖 2 ：使用邊緣檢測器卷積核的圖像的卷積。

卷積在物理和數學中很重要，因為它通過卷積定理定義了空間域和時域（位置（ 0 ， 30 處強度為 147 的像素）和頻域（振幅為 0 。 3 ，頻率為 30Hz ，相位為 60 度）之間的橋梁。這種橋是通過使用傅立葉變換來定義的：當你對核和特征映射都使用傅立葉變換時，卷積運算就大大簡化了（積分變成了乘法）。卷積的一些最快的 GPU 實現（例如 NVIDIA cuDNN 庫中的一些實現）目前使用傅立葉變換。

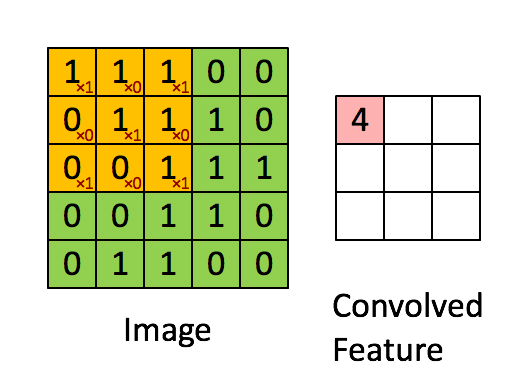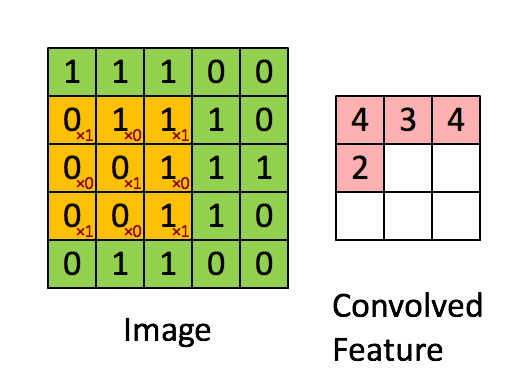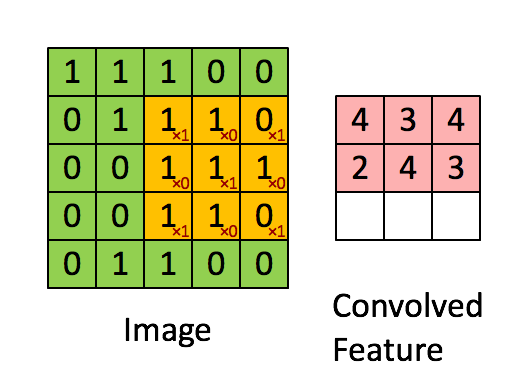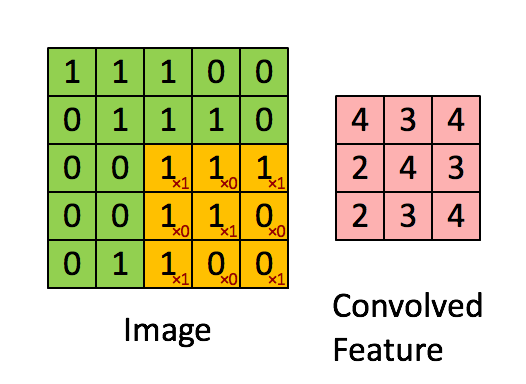
圖 3 ：通過在整個圖像上滑動圖像塊來計算卷積。將原始圖像（綠色）的一個圖像塊（黃色）乘以核（黃色斑塊中的紅色數字），并將其和寫入一個特征映射像素（卷積特征中的紅細胞）。圖片來源： 1 。

卷積可以描述信息的擴散，例如，將牛奶放入咖啡中而不攪拌時發生的擴散可以通過卷積操作精確地建模（像素向圖像中的輪廓擴散）。在量子力學中，它描述了當你測量粒子位置時量子粒子在某個位置的概率（像素位置的平均概率在輪廓處最高）。在概率論中，它描述了互相關，即重疊的兩個序列的相似程度（如果特征（例如鼻子）的像素在圖像（例如臉部）中重疊，則相似度很高）。在統計學中，它描述了一個標準化輸入序列上的加權移動平均值（輪廓線的權重大，其他所有的權重都很小）。還有許多其他的解釋。

對于深度學習，卷積的哪種解釋是正確的還不清楚，但目前最有用的解釋是：卷積濾波器可以解釋為特征檢測器，即輸入（特征映射）針對某個特征（核）進行過濾，如果在形象。這就是如何解釋圖像的互相關。

圖 4 ：圖像的互相關。卷積可以通過反轉核（倒置圖像）轉換為互相關。然后，內核可以被解釋為一個特征檢測器，其中檢測到的特征導致大輸出（白色）和小輸出（如果沒有特征存在）（黑色）。圖片取自 史蒂芬·史密斯 的優秀作品 關于數字信號處理的免費在線書籍 。

附加材料： 在深度學習中理解卷積

抽樣/子抽樣

池化是一個過程，它接受某個區域的輸入并將其減少到單個值（子采樣）。在 卷積神經網絡 中，這種集中的信息具有有用的特性，即傳出連接通常接收相似的信息（信息被“漏斗”地“導入”到下一個卷積層的輸入特征映射的正確位置）。這為旋轉和平移提供了基本的不變性。例如，如果一個圖像塊上的人臉不在圖像的中心，而是稍微平移了一下，它仍然可以正常工作，因為信息通過池化操作被導入到正確的位置，這樣卷積濾波器就可以檢測到人臉。

池區越大，信息就越濃縮，這就導致了更容易放入 GPU 內存的細長網絡。但是，如果池區域太大，就會丟棄太多的信息，并且預測性能會降低。

卷積神經網絡

卷積神經網絡，或優選卷積網絡或卷積網絡（術語“神經”具有誤導性；另請參見 人工神經元 ）使用卷積 層 （參見 卷積 ），它過濾輸入以獲取有用信息。這些卷積層具有學習的參數，以便自動調整這些濾波器以提取手頭任務的最有用信息（參見特征學習）。例如，在一般的目標識別任務中，過濾有關對象形狀的信息（對象通常具有非常不同的形狀），而對于鳥類識別任務，它更適合于提取有關鳥的顏色的信息（大多數鳥的形狀相似，但顏色不同）；這里的顏色更能區分鳥類）。卷積網絡會自動調整以找到這些任務的最佳特征。

通常，多個卷積層用于在每一層之后過濾圖像以獲得越來越多的抽象信息（參見層次特征）。

卷積網絡通常也使用池層（見 聯營 ），以獲得有限的平移和旋轉不變性（即使對象出現在不尋常的地方也能檢測到）。池化還可以減少內存消耗，從而允許使用更多的卷積層。

最近的卷積網絡使用初始模塊（見 開端 ），它使用 1 × 1 卷積核來進一步減少內存消耗，同時加快計算速度（從而提高訓練速度）。

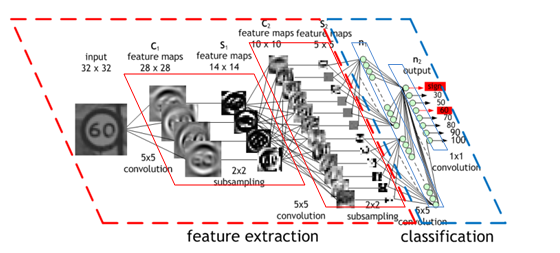
圖 5 ：一個交通標志的圖像被 4 個 5 × 5 的卷積核過濾，生成 4 個特征圖，這些特征圖通過最大池化進行二次采樣。下一層將 10 個 5 × 5 的卷積核應用于這些子采樣圖像，并再次將特征映射集中在一起。最后一層是一個完全連接的層，在這里所有生成的特征被組合并用于分類器（本質上是 logistic 回歸）。圖像由 莫里斯·皮曼 提供。

附加材料： 課程：機器學習的神經網絡：用神經網絡識別物體 。

開端

卷積網絡 中的初始模塊被設計為允許更深更大的 卷積 al 層 ，同時允許更有效的計算。這是通過使用較小的特征圖尺寸的 1 × 1 卷積來實現的，例如 192 個 28 × 28 尺寸的特征地圖可以通過 64 個 1 × 1 的卷積縮小為 64 個 28 × 28 的特征地圖。由于縮小了體積，這些 1 × 1 卷積可隨后得到 3 × 3 和 5 × 5 的較大卷積。除 1 × 1 卷積外，最大池化也可用于降維。

在初始模塊的輸出中，所有的大的卷積被連接成一個大的特征映射，然后被送入下一層（或初始模塊）。

附加材料： 卷積更深

第一部分結論

這是本次深度學習速成課程的第一部分。請盡快回來查看本系列的下兩個部分。在 第二部分 中，我將提供一個簡短的歷史概述，然后介紹如何訓練深層神經網絡。

關于作者

Tim Dettmers 是盧加諾大學信息學碩士生，在那里他從事深度學習研究。在此之前，他學習應用數學，并在自動化行業做了三年的軟件工程師。他經營著一個 關于深度學習的博客 ，并參加了 Kaggle 數據科學競賽，他的世界排名達到了 63 位。

審核編輯：郭婷