該視頻詳細講解了霍夫曼編碼提出的思路歷程。

目錄

故事背景

思路歷程

通信系統示意

衡量信息量

編碼和熵的關系

香農-馮諾編碼

霍夫曼的改進

故事背景1951 年，麻省理工學院的一名研究生 David Huffman 在 Robert Fano 的信息論課程上名列前茅。Fano 教授讓學生們在期末考試和學期論文間做出選擇，年輕的 Huffman 在一開始就選擇了學期論文。論文的題目如圖 1 所示，給定一組數字或符號，找到最有效的方法來使用二進制碼表示它們。

圖 1 Huffman 的學期論文題目

在基礎層面上，這是一個數據壓縮問題。事實上你在計算機上看到的文本和圖像本質上都是一組字母、數字或符號，如果將其歸結為最簡單的表示形式，那么它們其實都是一組 0 和 1 的組合，每個標準的數據類型都有一個標準的位表示。這個問題的本質是將它們壓縮成盡可能少的位數。這是一個自計算出現以來就存在的問題，但 Fano 沒有告訴學生的是，這在當時是信息論和數據壓縮領域的一個未解決的問題。Huffman 在研究生時解決了這個問題，他的解決方案就是大名鼎鼎的霍夫曼編碼算法。

圖 2 數據壓縮問題

思路歷程通信系統示意在一個通信系統中，我們通常有一個信息發送方和信息接受方。發送方想要通過網絡向接受方發送一些原始信息，但在網絡中唯一有意義的信息是二進制比特。因此，發送方必須根據符號和二進制代碼間的某種映射對原始信息進行編碼。而接收方需要對二進制代碼進行解碼以恢復原始信息。

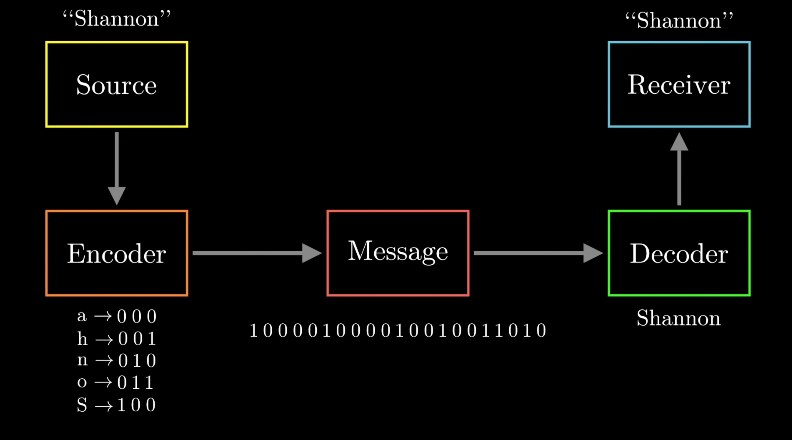
圖 3 通信系統示意圖

編碼方法一般針對從原始信息到二進制碼的映射進行優化，從原始信息到二進制碼的映射有一些內在要求。一是每個符號必須被映射到唯一的二進制碼，二是接收方必須能夠準確解碼出原始信息。霍夫曼編碼算法完全符合這些要求。

衡量信息量對數據進行壓縮時，我們需要考慮一種平衡。如果使用太多的比特表示符號，那么會導致冗余;如果使用太少的比特表示，則會導致信息丟失，因此最優的無損壓縮算法應該在兩者之間找到平衡。那么我們首先需要知道在不丟失原始信息的情況下，最大的壓縮率是多少。對于這個問題，我們可以理解為，需要找到在原始信息中包含的真正的信息量是多少。那我們如何衡量信息量的多少呢?

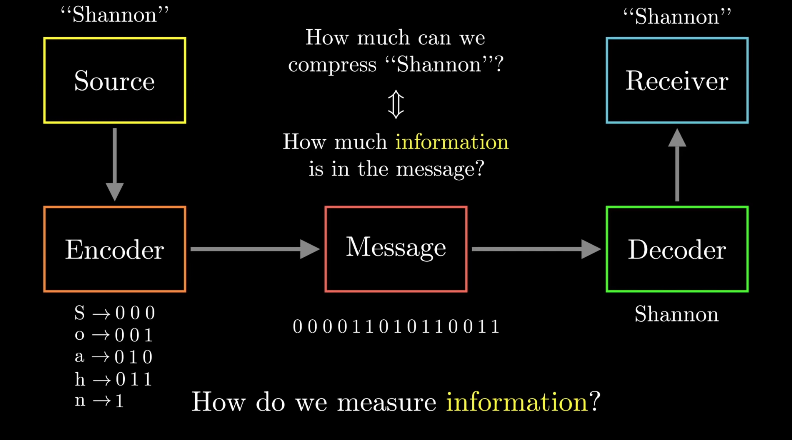
圖 4 如何衡量信息量

一句話中包含的信息量與文字的長度并沒有直接的關聯。如圖 5 所示，對于這兩句話來說，顯然在沙哈拉沙漠下雪所包含的信息量更大，因為在沙漠下雪的概率極小。因此可以想到，事件相關的信息量與事件發生的概率有很大的關系。

圖 5 信息量例子

香農根據信息的性質總結了四個定律：

信息量的大小跟事件發生的概率反相關

信息量永遠大于等于 0，因為事件的發生不會導致信息損失

如果一件事發生的概率是 100%，那么它不包含任何信息量

如果兩個不相關事件被分別觀察到，那么它包含的信息量應該是這兩個事件單獨信息量的和

香農根據這四個定律給出了自信息的定義。當信息以 bit 為單位時，log 函數的底數取 2。

圖 6 自信息定義

但香農更偉大的貢獻在于將自信息推廣到了更廣的分布上，給出了信息熵的概念，也就是著名的香農定理。香農定理作為信息論的基礎，給出了衡量信息量的標準公式。

圖 7 香農定理

編碼和熵的關系當衡量不同編碼方式的性能時，我們需要計算不同編碼方式的平均字符長度。在信息論中，我們通常將符號編碼的長度根據符號出現的概率進行加權求和得到平均的符號長度。香農發現，無論對符號進行哪種方式的無損壓縮編碼，它的長度總是大于等于信息熵，這就是香農的源編碼定理。

圖 8 香農源編碼定理

香農-馮諾編碼香農-馮諾編碼首先對符號按照概率進行升序排列。然后找到最好的分割方法將符號分為兩組，使得兩組的符號概率和盡可能接近。之后對每個組進行遞歸劃分，直到每個符號都被單獨分為一組。

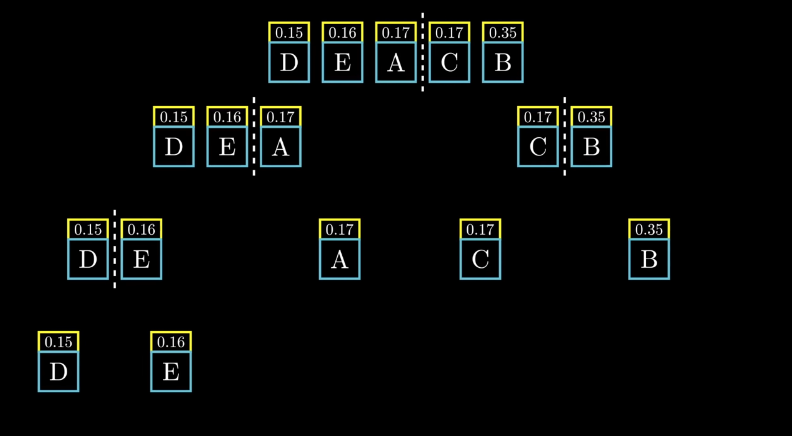
圖 9 香農-馮諾編碼分組

分完組之后，編碼就變得很簡單了。從頭部向下，如果向左，那么對符號編碼添加 0，向右走則添加 1，最終可以得到所有符號的二進制編碼。而且對于這個樹形圖的表示，在解碼端是不會存在歧義的。

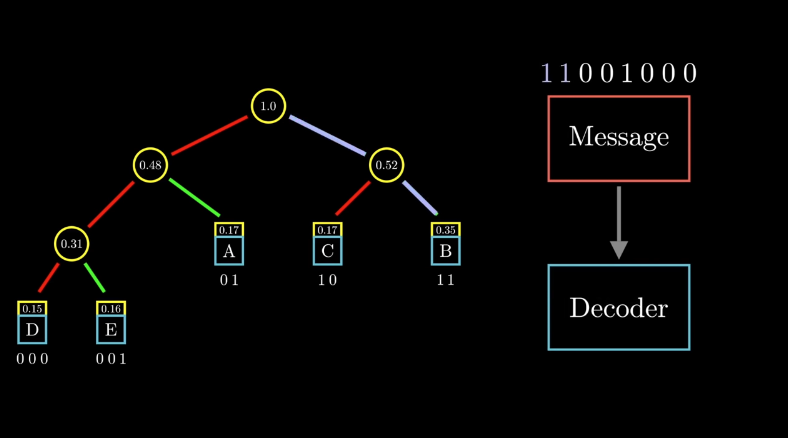
圖 10 香農-馮諾編碼樹形圖

霍夫曼的改進但是香農-馮諾編碼并不總是最優的，在思考最小化平均符號長度時，可以想到，兩個最不可能出現的符號應該出現在二叉樹的最底部，也就是編碼長度最長的地方。這符合我們的直覺，那就是最不常出現的符號應該具有更長的編碼長度。因此我們可以想到，先將兩個最不可能出現的符號放在最底部去構建一個二叉樹，然后將這個二叉樹的根節點視作一個新的符號節點，該符號節點的概率是兩個子節點的和。然后對剩余的符號節點做相同的操作，直到構建出一個完整的二叉樹，這就是霍夫曼編碼。

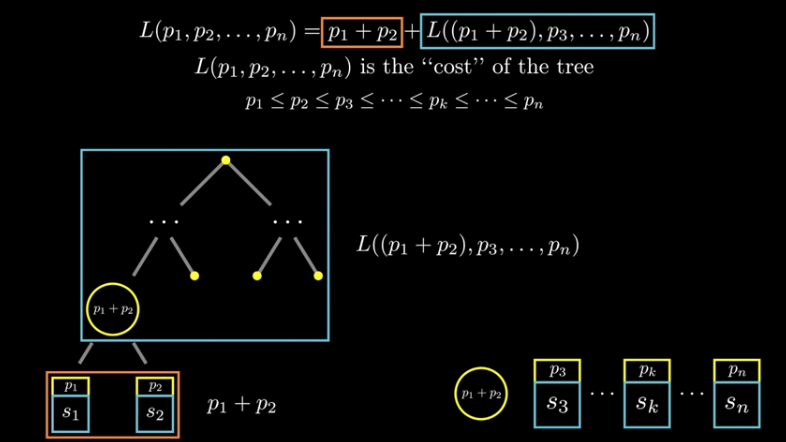
圖 11 霍夫曼的改進1

圖 12 霍夫曼的改進2

原文標題：[基礎知識] 霍夫曼編碼

文章出處：【微信公眾號：LiveVideoStack】歡迎添加關注!文章轉載請注明出處。