材料的電磁特性是所有電子材料繞不過去的話題。今天,我來跟小伙伴們一起聊聊材料電磁特性中的介電常數。
1
從麥克斯韋方程組說起:
既然說到了電子、電磁,就一定要說麥克斯韋方程組了。記得前幾年看過一個帖子,選出了人類歷史上十個最偉大的公式,麥克斯韋方程組當仁不讓位列其中。麥克斯韋老先生推導出這個方程組后,預言了電磁波的存在;愛因斯坦更是根據麥克斯韋方程組提出了狹義相對論。麥克斯韋可以說是所有電子相關專業同學的親祖師爺了。
麥克斯韋方程組有積分形式和微分形式,有興趣的小伙伴可以找來看看,很容易看暈的。看暈了的小伙伴先別著急放棄。說實話,這方程組我看著也暈。所以我們今天不去講這個偉大的方程組。我們的重點的是本構方程。僅有麥克斯韋方程組還不足以求解,還必須引入描述材料電磁特性的本構方程:
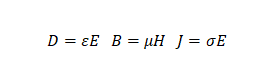
這三個方程看起來好欺負多了吧,今天,我們就一起聊聊第一個本構方程中的這個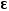 ,介電常數。
,介電常數。
2
介電常數是個啥? 介電常數在PCB行業中習慣叫Dk和Df,這個我們一會兒再詳細聊,先來看看它的英文。在英文中有一個單詞(permittivity)和一個詞組(dielectricconstant)都表示介電常數,而“dielectricconstant”直譯過來就是“電介質常數”,由此可見,介電常數描述的是絕緣體在電場中的特性。我們先來回憶一下大學物理中的庫倫定律。根據庫倫定律,一個電荷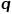 ,在真空中產生的電場強度
,在真空中產生的電場強度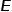 為:
為:
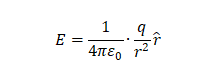
在這里,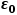 是物理學中的一個基本物理常量,稱為真空介電常數,其數值為:
是物理學中的一個基本物理常量,稱為真空介電常數,其數值為:
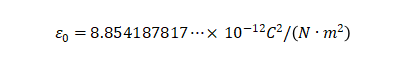
我們再回憶一下,一個導體(金屬),放在靜電場中會發生什么?
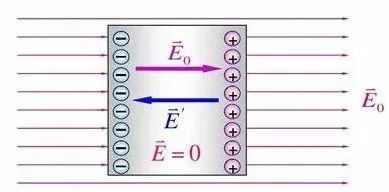
靜電場中的導體(圖片來自網絡) 由于金屬中有大量的自由電荷(電子),會在外加電場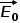 作用下移動,在金屬表面形成感應電荷,而感應電荷產生的感應電場
作用下移動,在金屬表面形成感應電荷,而感應電荷產生的感應電場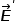 與外加電場
與外加電場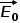 大小相等,方向相反。所以在金屬內部感應電場與外加電場互相抵消,總場強為零,也就是說金屬內部是不存在電場的。把絕緣體(電介質材料)放在靜電場中會發生什么呢?先說結論:跟金屬一樣的是,會在電介質表面出現感應電荷;不一樣的是感應電荷產生的感應電場不足以完全抵消外加電場。小伙伴們可能會奇怪?絕緣體中沒有自由電荷,為啥也會感應出電荷?絕緣體的分子按是否有極性,可以分成兩大類:無極分子和有極分子。
大小相等,方向相反。所以在金屬內部感應電場與外加電場互相抵消,總場強為零,也就是說金屬內部是不存在電場的。把絕緣體(電介質材料)放在靜電場中會發生什么呢?先說結論:跟金屬一樣的是,會在電介質表面出現感應電荷;不一樣的是感應電荷產生的感應電場不足以完全抵消外加電場。小伙伴們可能會奇怪?絕緣體中沒有自由電荷,為啥也會感應出電荷?絕緣體的分子按是否有極性,可以分成兩大類:無極分子和有極分子。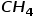 是典型的無極分子,其特點是正電荷的幾何中心與負電荷的幾何中心重合,整體上沒有電矩;而
是典型的無極分子,其特點是正電荷的幾何中心與負電荷的幾何中心重合,整體上沒有電矩;而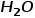 的正電荷與負電荷的幾何中心不重合,整體上表現出一個電矩。
的正電荷與負電荷的幾何中心不重合,整體上表現出一個電矩。

無極分子和有極分子(圖片來自網絡) 無極分子材料在沒有外加電場時表面為電中性,但是在外加靜電場時,分子中的正電荷和負電荷會向不同方向偏移,產生電矩,稱為位移極化。位移極化產生的電矩在內部互相抵消,而在材料的表面產生電荷。
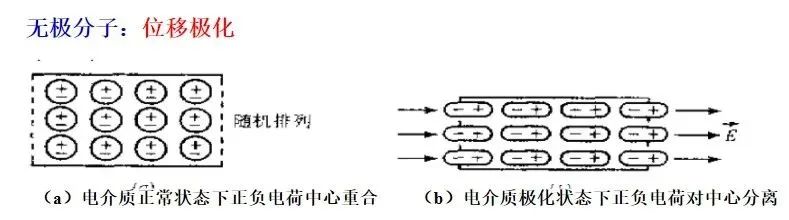
位移極化(圖片來自網絡) 有極分子雖然每個分子是有極性的,但在沒有外加靜電場時,大量分子隨機運動,宏觀上表現為電中性,但在外加靜電場時,分子排列發生一定的改變,趨向于一致,從而在材料表面產生電荷,這一過程稱為取向極化。
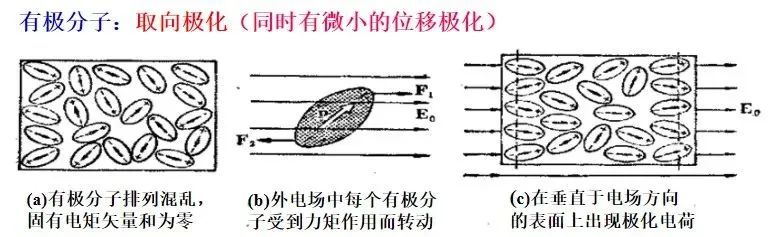
取向極化(圖片來自網絡) 現在我們知道了,電介質材料在靜電場中也會在表面形成感應電荷,這一點與金屬材料是相同的。但是在電介質材料表面的感應電荷產生的感應電場不足以抵消掉外加電場,所以電介質材料內部的總電場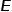 比外加電場小,但不為零。我們可以計算出,一個電荷
比外加電場小,但不為零。我們可以計算出,一個電荷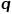 ,在電介質中產生的電場強度
,在電介質中產生的電場強度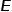 為:
為: 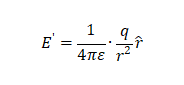 這里的
這里的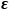 我們稱為這種電介質材料的介電常數,工程上,我們經常會把這個值對
我們稱為這種電介質材料的介電常數,工程上,我們經常會把這個值對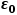 做歸一化,歸一化后的值稱為相對介電常數
做歸一化,歸一化后的值稱為相對介電常數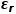 ,是一個無量綱的值:
,是一個無量綱的值: 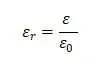 由此可以看出,材料的相對介電常數(工程上經常直接簡稱為介電常數)是材料本身固有的屬性。
由此可以看出,材料的相對介電常數(工程上經常直接簡稱為介電常數)是材料本身固有的屬性。
敲黑板畫一下重點:一個電荷,在真空中產生的電場為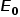 ,在金屬中產生的電場為0,而在電介質材料中產生的電場為
,在金屬中產生的電場為0,而在電介質材料中產生的電場為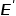 ,
,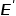 小于
小于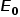 ,其比值就是這種材料的相對介電常數。
,其比值就是這種材料的相對介電常數。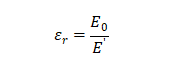 上面討論的是介質在靜電場條件下的特性,在交流電場下,情況會變得更復雜。在這我們不做詳細的討論了,有興趣的同學可以參考方俊鑫,殷之文的《電介質物理學》。簡單的說,在高頻電場作用下絕緣材料會產生位移電流,且位移電流方向與電場方向不正交,消耗了功率,引起了損耗。因此,在高頻,材料的相對介電常數為復數
上面討論的是介質在靜電場條件下的特性,在交流電場下,情況會變得更復雜。在這我們不做詳細的討論了,有興趣的同學可以參考方俊鑫,殷之文的《電介質物理學》。簡單的說,在高頻電場作用下絕緣材料會產生位移電流,且位移電流方向與電場方向不正交,消耗了功率,引起了損耗。因此,在高頻,材料的相對介電常數為復數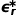 :
:
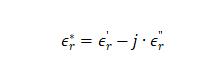
其中的虛部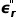 代表了材料在高頻的損耗。把復數
代表了材料在高頻的損耗。把復數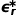 畫在復數坐標軸上,可以看到該復數的相位
畫在復數坐標軸上,可以看到該復數的相位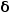 的正切值為:
的正切值為:
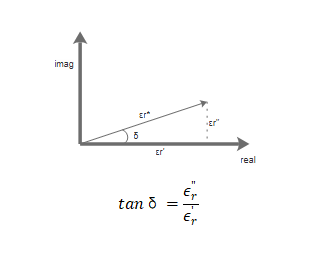
在工程上,常用這個值表征材料的損耗,稱為損耗角正切。在PCB行業,習慣上把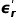 稱為Dk(Dielectric Constant),而把損耗角正切
稱為Dk(Dielectric Constant),而把損耗角正切 稱為Df(Dissipation Factor,耗散因子)。
稱為Df(Dissipation Factor,耗散因子)。
3
介電常數有啥特性? 前面已經說過了,介電常數主要與材料本身的分子結構和排列方式有關,所以是材料本身固有的屬性,一般不會改變。對于混合材料就比較復雜了。比如如果材料放置了一段時間后吸水,會引起介電常數的變化。大多數材料的介電常數跟方向無關,我們稱為各向同性材料。也有些材料不同,比如一些編織材料,平行于編織面和垂直于編織面的介電常數是不一樣的,稱為各向異性材料。還有一類特殊的材料也是各向異性的,比如鐵電體和向量型液晶。材料的介電常數是頻率的函數,也就是說不同頻率上的介電常數是不同的。
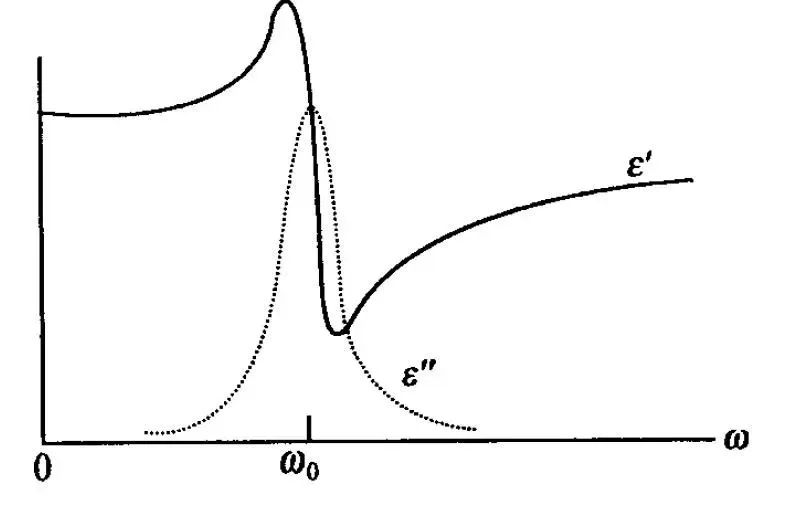
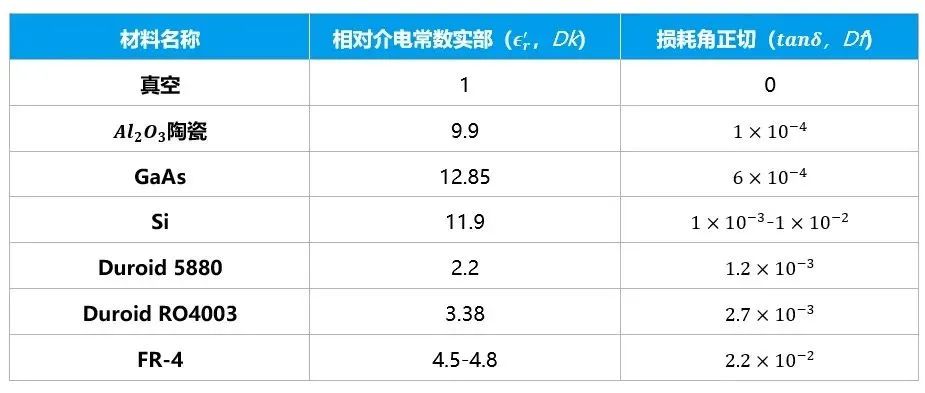
復介電常數隨頻率的變化 此外,材料的介電常數也是隨溫度變化。下表給出了一些材料在10 GHz,室溫下的相對介電常數:
4
介電常數會影響啥? 既然叫介“電”常數,那么它一定會對電信號產生影響。影響之一:電容介電常數其實還有另一個名字-電容率。從名字就可以看出,材料的介電常數會影響電容的電容量。高中物理我們學習過平行板電容器:兩塊平行的金屬板,中間夾以電介質薄層。平行板電容器的電容量(忽略邊緣效應): 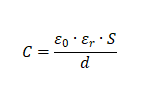 式中
式中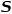 為平行金屬板相對的面積,
為平行金屬板相對的面積,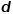 為平行金屬板的距離,也就是電介質材料的厚度。
為平行金屬板的距離,也就是電介質材料的厚度。
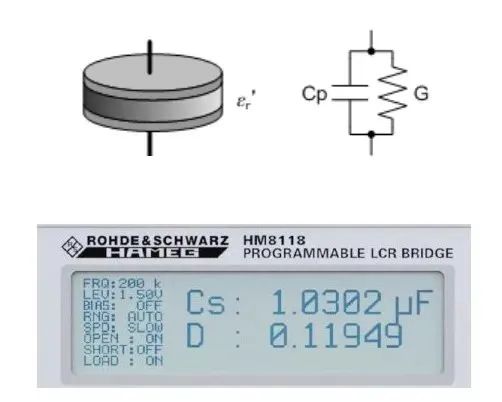
理想的電容是沒有損耗的,但是由于電介質材料存在損耗(復介電常數的虛部),因此實際的電容的等效電路為一個理想電容和一個電阻并聯,而電容的損耗用耗散因子D來描述:
影響二:電磁波的傳播速度小伙伴們都知道,電磁波是以光速傳播的。我們常說光速是299792458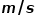 ,或者簡化為
,或者簡化為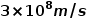 。但咱們要注意,這個光速是電磁波在真空中傳播的光速。當電磁波在電介質材料中傳播時,速度會變慢,而變慢多少是由介電常數決定的:
。但咱們要注意,這個光速是電磁波在真空中傳播的光速。當電磁波在電介質材料中傳播時,速度會變慢,而變慢多少是由介電常數決定的: 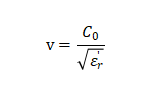 式中
式中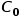 是真空中的光速。我們知道光速等于電磁波的頻率乘以電磁波的波長。當電磁波在電介質材料中傳播時,電磁波的頻率不會變化,而波長會變短。電磁波在電介質材料中傳播時,能量會逐漸降低,這種衰減就是由于復介電常數的虛部引起的。
是真空中的光速。我們知道光速等于電磁波的頻率乘以電磁波的波長。當電磁波在電介質材料中傳播時,電磁波的頻率不會變化,而波長會變短。電磁波在電介質材料中傳播時,能量會逐漸降低,這種衰減就是由于復介電常數的虛部引起的。
影響三:微波傳輸線的特征阻抗微波傳輸線是微波技術中的概念,用于傳輸微波信號。微波傳輸線最重要的指標就是其特征阻抗,而各種微波傳輸線的特征阻抗都與其中填充的電介質的介電常數有關。以常見的同軸傳輸線為例:
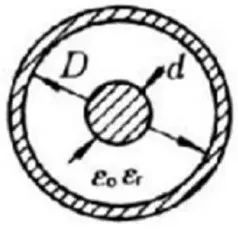
同軸傳輸線截面 同軸傳輸線有外導體、內導體和之間填充的電介質材料組成,他的特征阻抗為: 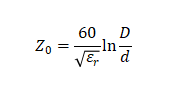 介電常數的測量實際上就是利用了其對電信號的影響來進行的,這一部分內容請參考之前的文章《你與漫威英雄的差距可不止一面振金的盾牌,還有......》和《麻瓜的隱形斗篷怎么做?還得先從材料電磁特性測試開始》
介電常數的測量實際上就是利用了其對電信號的影響來進行的,這一部分內容請參考之前的文章《你與漫威英雄的差距可不止一面振金的盾牌,還有......》和《麻瓜的隱形斗篷怎么做?還得先從材料電磁特性測試開始》
關于介電常數的那些事,我們今天就聊到這里,小伙伴們還有哪些疑問呢?歡迎給我們留言。 參考書目:《電介質物理學》(第二版) 殷之文主編 科學出版社《電磁學》趙凱華 陳熙謀 高等教育出版社
審核編輯 :李倩
-
電磁
+關注
關注
15文章
1075瀏覽量
51726 -
介電常數
+關注
關注
1文章
105瀏覽量
18410
原文標題:【精選知識講堂】聊聊介電常數那些事
文章出處:【微信號:羅德與施瓦茨中國,微信公眾號:羅德與施瓦茨中國】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
介電常數在高頻信號中的表現
如何選擇適合的材料以滿足介電常數要求
介電常數與電容器性能的關系
介電常數與頻率的關系 影響介電常數的因素有哪些
如何測量介電常數 介電常數在電磁波中的作用
介電常數對電子設備的影響
介電常數的定義及應用 不同材料的介電常數比較
電路板設計中要考慮的PCB材料特性







 材料電磁特性中的介電常數
材料電磁特性中的介電常數
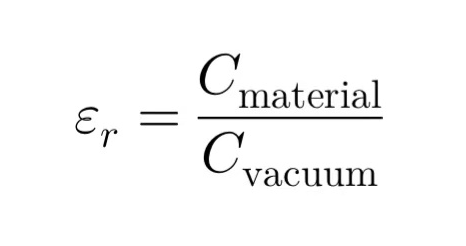











評論