算法一：快速排序法

快速排序是由東尼·霍爾所發(fā)展的一種排序算法。在平均狀況下，排序 n 個(gè)項(xiàng)目要Ο（n log n）次比較。在最壞狀況下則需要Ο（n2）次比較，但這種狀況并不常見(jiàn)。事實(shí)上，快速排序通常明顯比其他Ο（n log n） 算法更快，因?yàn)樗膬?nèi)部循環(huán)（inner loop）可以在大部分的架構(gòu)上很有效率地被實(shí)現(xiàn)出來(lái)。

快速排序使用分治法（Divide and conquer）策略來(lái)把一個(gè)串行（list）分為兩個(gè)子串行（sub-lists）。

》 》 》 》

算法步驟

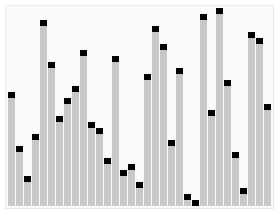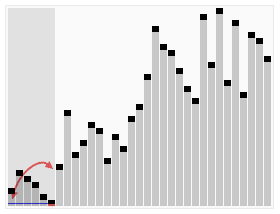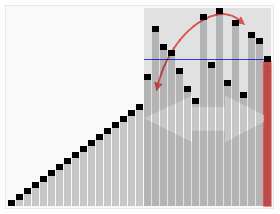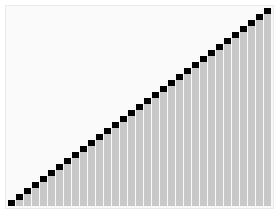
1 從數(shù)列中挑出一個(gè)元素，稱為 “基準(zhǔn)”（pivot），

2 重新排序數(shù)列，所有元素比基準(zhǔn)值小的擺放在基準(zhǔn)前面，所有元素比基準(zhǔn)值大的擺在基準(zhǔn)的后面（相同的數(shù)可以到任一邊）。在這個(gè)分區(qū)退出之后，該基準(zhǔn)就處于數(shù)列的中間位置。這個(gè)稱為分區(qū)（partition）操作。

3 遞歸地（recursive）把小于基準(zhǔn)值元素的子數(shù)列和大于基準(zhǔn)值元素的子數(shù)列排序。

遞歸的最底部情形，是數(shù)列的大小是零或一，也就是永遠(yuǎn)都已經(jīng)被排序好了。雖然一直遞歸下去，但是這個(gè)算法總會(huì)退出，因?yàn)樵诿看蔚牡╥teration）中，它至少會(huì)把一個(gè)元素?cái)[到它最后的位置去。

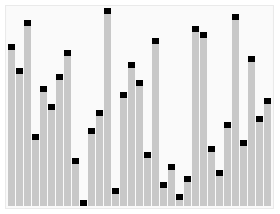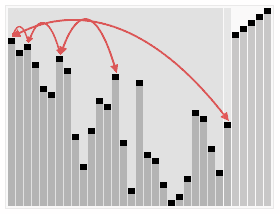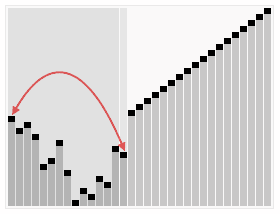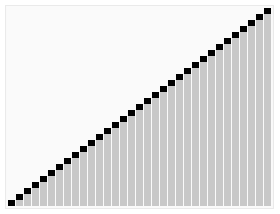
算法二：堆排序算法

堆排序（Heapsort）是指利用堆這種數(shù)據(jù)結(jié)構(gòu)所設(shè)計(jì)的一種排序算法。堆積是一個(gè)近似完全二叉樹(shù)的結(jié)構(gòu)，并同時(shí)滿足堆積的性質(zhì)：即子結(jié)點(diǎn)的鍵值或索引總是小于（或者大于）它的父節(jié)點(diǎn)。

堆排序的平均時(shí)間復(fù)雜度為Ο（nlogn） 。

》 》 》 》

算法步驟

創(chuàng)建一個(gè)堆H［0..n-1］

把堆首（最大值）和堆尾互換

3. 把堆的尺寸縮小1，并調(diào)用shift_down（0），目的是把新的數(shù)組頂端數(shù)據(jù)調(diào)整到相應(yīng)位置

4. 重復(fù)步驟2，直到堆的尺寸為1

算法三：規(guī)并排序

歸并排序（Merge sort，臺(tái)灣譯作：合并排序）是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法（Divide and Conquer）的一個(gè)非常典型的應(yīng)用。

》 》 》 》

算法步驟

1. 申請(qǐng)空間，使其大小為兩個(gè)已經(jīng)排序序列之和，該空間用來(lái)存放合并后的序列

2. 設(shè)定兩個(gè)指針，最初位置分別為兩個(gè)已經(jīng)排序序列的起始位置

3. 比較兩個(gè)指針?biāo)赶虻脑兀x擇相對(duì)小的元素放入到合并空間，并移動(dòng)指針到下一位置

4. 重復(fù)步驟3直到某一指針達(dá)到序列尾

5. 將另一序列剩下的所有元素直接復(fù)制到合并序列尾

算法四：二分查找算法

二分查找算法是一種在有序數(shù)組中查找某一特定元素的搜索算法。搜素過(guò)程從數(shù)組的中間元素開(kāi)始，如果中間元素正好是要查找的元素，則搜 素過(guò)程結(jié)束；如果某一特定元素大于或者小于中間元素，則在數(shù)組大于或小于中間元素的那一半中查找，而且跟開(kāi)始一樣從中間元素開(kāi)始比較。如果在某一步驟數(shù)組 為空，則代表找不到。這種搜索算法每一次比較都使搜索范圍縮小一半。折半搜索每次把搜索區(qū)域減少一半，時(shí)間復(fù)雜度為Ο（logn）

算法五：BFPRT（線性排查）

BFPRT算法解決的問(wèn)題十分經(jīng)典，即從某n個(gè)元素的序列中選出第k大（第k小）的元素，通過(guò)巧妙的分 析，BFPRT可以保證在最壞情況下仍為線性時(shí)間復(fù)雜度。該算法的思想與快速排序思想相似，當(dāng)然，為使得算法在最壞情況下，依然能達(dá)到o（n）的時(shí)間復(fù)雜 度，五位算法作者做了精妙的處理。

》 》 》 》

算法步驟

1. 將n個(gè)元素每5個(gè)一組，分成n/5（上界）組。

2. 取出每一組的中位數(shù)，任意排序方法，比如插入排序。

3. 遞歸的調(diào)用selection算法查找上一步中所有中位數(shù)的中位數(shù)，設(shè)為x，偶數(shù)個(gè)中位數(shù)的情況下設(shè)定為選取中間小的一個(gè)。

4. 用x來(lái)分割數(shù)組，設(shè)小于等于x的個(gè)數(shù)為k，大于x的個(gè)數(shù)即為n-k。

5. 若i==k，返回x；若i《k，在小于x的元素中遞歸查找第i小的元素；若i》k，在大于x的元素中遞歸查找第i-k小的元素。 《/k，在小于x的元素中遞歸查找第i小的元素；若i》

終止條件：n=1時(shí)，返回的即是i小元素。

算法六：DFS（深度優(yōu)先搜索）

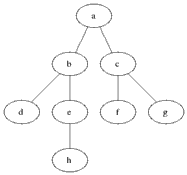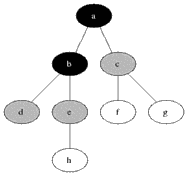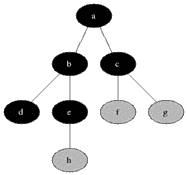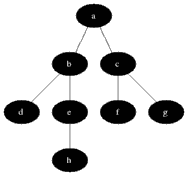
深度優(yōu)先搜索算法（Depth-First-Search），是搜索算法的一種。它沿著樹(shù)的深度遍歷樹(shù)的節(jié)點(diǎn)，盡可能深的搜索樹(shù)的分 支。當(dāng)節(jié)點(diǎn)v 的所有邊都己被探尋過(guò)，搜索將回溯到發(fā)現(xiàn)節(jié)點(diǎn)v的那條邊的起始節(jié)點(diǎn)。這一過(guò)程一直進(jìn)行到已發(fā)現(xiàn)從源節(jié)點(diǎn)可達(dá)的所有節(jié)點(diǎn)為止。如果還存在未被發(fā) 現(xiàn)的節(jié)點(diǎn)，則選擇其中一個(gè)作為源節(jié)點(diǎn)并重復(fù)以上過(guò)程，整個(gè)進(jìn)程反復(fù)進(jìn)行直到所有節(jié)點(diǎn)都被訪問(wèn)為止。DFS屬于盲目搜索。

深度優(yōu)先搜索是圖論中的經(jīng)典算法，利用深度優(yōu)先搜索算法可以產(chǎn)生目標(biāo)圖的相應(yīng)拓?fù)渑判虮恚猛負(fù)渑判虮砜梢苑奖愕慕鉀Q很多相關(guān)的圖論問(wèn)題，如最大路徑問(wèn)題等等。一般用堆數(shù)據(jù)結(jié)構(gòu)來(lái)輔助實(shí)現(xiàn)DFS算法。

》 》 》 》算法步驟

深度優(yōu)先遍歷圖算法步驟：

1. 訪問(wèn)頂點(diǎn)v；

2. 依次從v的未被訪問(wèn)的鄰接點(diǎn)出發(fā)，對(duì)圖進(jìn)行深度優(yōu)先遍歷；直至圖中和v有路徑相通的頂點(diǎn)都被訪問(wèn)；

3. 若此時(shí)圖中尚有頂點(diǎn)未被訪問(wèn)，則從一個(gè)未被訪問(wèn)的頂點(diǎn)出發(fā)，重新進(jìn)行深度優(yōu)先遍歷，直到圖中所有頂點(diǎn)均被訪問(wèn)過(guò)為止。

上述描述可能比較抽象，舉個(gè)實(shí)例：

DFS 在訪問(wèn)圖中某一起始頂點(diǎn) v 后，由 v 出發(fā)，訪問(wèn)它的任一鄰接頂點(diǎn) w1；再?gòu)?w1 出發(fā)，訪問(wèn)與 w1鄰 接但還沒(méi)有訪問(wèn)過(guò)的頂點(diǎn) w2；然后再?gòu)?w2 出發(fā)，進(jìn)行類似的訪問(wèn)，… 如此進(jìn)行下去，直至到達(dá)所有的鄰接頂點(diǎn)都被訪問(wèn)過(guò)的頂點(diǎn) u 為止。

接著，退回一步，退到前一次剛訪問(wèn)過(guò)的頂點(diǎn)，看是否還有其它沒(méi)有被訪問(wèn)的鄰接頂點(diǎn)。如果有，則訪問(wèn)此頂點(diǎn)，之后再?gòu)拇隧旤c(diǎn)出發(fā)，進(jìn)行與前述類似的訪問(wèn)；如果沒(méi)有，就再退回一步進(jìn)行搜索。重復(fù)上述過(guò)程，直到連通圖中所有頂點(diǎn)都被訪問(wèn)過(guò)為止。

算法七：BFS（廣度優(yōu)先搜索）

廣度優(yōu)先搜索算法（Breadth-First-Search），是一種圖形搜索算法。簡(jiǎn)單的說(shuō)，BFS是從根節(jié)點(diǎn)開(kāi)始，沿著樹(shù)（圖）的寬度遍歷樹(shù)（圖）的節(jié)點(diǎn)。如果所有節(jié)點(diǎn)均被訪問(wèn)，則算法中止。BFS同樣屬于盲目搜索。一般用隊(duì)列數(shù)據(jù)結(jié)構(gòu)來(lái)輔助實(shí)現(xiàn)BFS算法。

》 》 》 》

算法步驟

1. 首先將根節(jié)點(diǎn)放入隊(duì)列中。

2. 從隊(duì)列中取出第一個(gè)節(jié)點(diǎn)，并檢驗(yàn)它是否為目標(biāo)。

如果找到目標(biāo)，則結(jié)束搜尋并回傳結(jié)果。

否則將它所有尚未檢驗(yàn)過(guò)的直接子節(jié)點(diǎn)加入隊(duì)列中。

3. 若隊(duì)列為空，表示整張圖都檢查過(guò)了——亦即圖中沒(méi)有欲搜尋的目標(biāo)。結(jié)束搜尋并回傳“找不到目標(biāo)”。

4. 重復(fù)步驟2。

算法八：Dijkstra

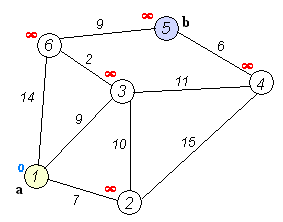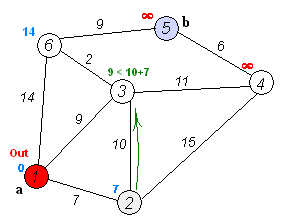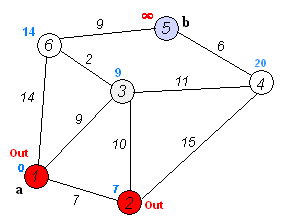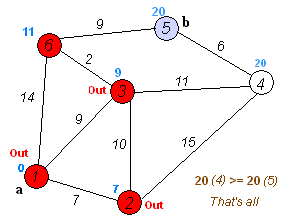
戴克斯特拉算法（Dijkstra’s algorithm）是由荷蘭計(jì)算機(jī)科學(xué)家艾茲赫爾·戴克斯特拉提出。迪科斯徹算法使用了廣度優(yōu)先搜索解決非負(fù)權(quán)有向圖的單源最短路徑問(wèn)題，算法最終得到一個(gè)最短路徑樹(shù)。該算法常用于路由算法或者作為其他圖算法的一個(gè)子模塊。

該算法的輸入包含了一個(gè)有權(quán)重的有向圖 G，以及G中的一個(gè)來(lái)源頂點(diǎn) S。我們以 V 表示 G 中所有頂點(diǎn)的集合。每一個(gè)圖中的邊，都是兩個(gè)頂點(diǎn)所形成的有序元素對(duì)。（u， v） 表示從頂點(diǎn) u 到 v 有路徑相連。我們以 E 表示G中所有邊的集合，而邊的權(quán)重則由權(quán)重函數(shù) w： E → ［0， ∞］ 定義。因此，w（u， v） 就是從頂點(diǎn) u 到頂點(diǎn) v 的非負(fù)權(quán)重（weight）。邊的權(quán)重可以想像成兩個(gè)頂點(diǎn)之間的距離。任兩點(diǎn)間路徑的權(quán)重，就是該路徑上所有邊的權(quán)重總和。已知有 V 中有頂點(diǎn) s 及 t，Dijkstra 算法可以找到 s 到 t的最低權(quán)重路徑（例如，最短路徑）。這個(gè)算法也可以在一個(gè)圖中，找到從一個(gè)頂點(diǎn) s 到任何其他頂點(diǎn)的最短路徑。對(duì)于不含負(fù)權(quán)的有向圖，Dijkstra算法是目前已知的最快的單源最短路徑算法。

》 》 》 》

算法步驟

1. 初始時(shí)令 S={V0}，T={其余頂點(diǎn)}，T中頂點(diǎn)對(duì)應(yīng)的距離值

若存在，d（V0，Vi）為弧上的權(quán)值

若不存在，d（V0，Vi）為∞

2. 從T中選取一個(gè)其距離值為最小的頂點(diǎn)W且不在S中，加入S

3. 對(duì)其余T中頂點(diǎn)的距離值進(jìn)行修改：若加進(jìn)W作中間頂點(diǎn)，從V0到Vi的距離值縮短，則修改此距離值

重復(fù)上述步驟2、3，直到S中包含所有頂點(diǎn)，即W=Vi為止

算法九：動(dòng)態(tài)規(guī)劃算法

動(dòng)態(tài)規(guī)劃（Dynamic programming）是一種在數(shù)學(xué)、計(jì)算機(jī)科學(xué)和經(jīng)濟(jì)學(xué)中使用的，通過(guò)把原問(wèn)題分解為相對(duì)簡(jiǎn)單的子問(wèn)題的方式求解復(fù)雜問(wèn)題的方法。動(dòng)態(tài)規(guī)劃常常適用于有重疊子問(wèn)題和最優(yōu)子結(jié)構(gòu)性質(zhì)的問(wèn)題，動(dòng)態(tài)規(guī)劃方法所耗時(shí)間往往遠(yuǎn)少于樸素解法。

動(dòng)態(tài)規(guī)劃背后的基本思想非常簡(jiǎn)單。大致上，若要解一個(gè)給定問(wèn)題，我們需要解其不同部分（即子問(wèn)題），再合并子問(wèn)題的解以得出原問(wèn)題的解。通常許多 子問(wèn)題非常相似，為此動(dòng)態(tài)規(guī)劃法試圖僅僅解決每個(gè)子問(wèn)題一次，從而減少計(jì)算量：一旦某個(gè)給定子問(wèn)題的解已經(jīng)算出，則將其記憶化存儲(chǔ)，以便下次需要同一個(gè) 子問(wèn)題解之時(shí)直接查表。這種做法在重復(fù)子問(wèn)題的數(shù)目關(guān)于輸入的規(guī)模呈指數(shù)增長(zhǎng)時(shí)特別有用。

關(guān)于動(dòng)態(tài)規(guī)劃最經(jīng)典的問(wèn)題當(dāng)屬背包問(wèn)題。

》 》 》 》

算法步驟

1. 最優(yōu)子結(jié)構(gòu)性質(zhì)。如果問(wèn)題的最優(yōu)解所包含的子問(wèn)題的解也是最優(yōu)的，我們就稱該問(wèn)題具有最優(yōu)子結(jié)構(gòu)性質(zhì)（即滿足最優(yōu)化原理）。最優(yōu)子結(jié)構(gòu)性質(zhì)為動(dòng)態(tài)規(guī)劃算法解決問(wèn)題提供了重要線索。

2. 子問(wèn)題重疊性質(zhì)。子問(wèn)題重疊性質(zhì)是指在用遞歸算法自頂向下對(duì)問(wèn)題進(jìn)行求解時(shí)，每次產(chǎn)生的子問(wèn)題并不總是新問(wèn)題，有些子問(wèn)題會(huì)被重復(fù)計(jì)算多次。動(dòng)態(tài)規(guī)劃算法正是利用了這種子問(wèn)題的重疊性質(zhì)，對(duì)每一個(gè)子問(wèn)題只計(jì)算一次，然后將其計(jì)算結(jié)果保存在一個(gè)表格中，當(dāng)再次需要計(jì)算已經(jīng)計(jì)算過(guò)的子問(wèn)題時(shí)，只是 在表格中簡(jiǎn)單地查看一下結(jié)果，從而獲得較高的效率。

算法十：樸素貝葉斯分類算法

樸素貝葉斯分類算法是一種基于貝葉斯定理的簡(jiǎn)單概率分類算法。貝葉斯分類的基礎(chǔ)是概率推理，就是在各種條件的存在不確定，僅知其出現(xiàn)概率的情況下， 如何完成推理和決策任務(wù)。概率推理是與確定性推理相對(duì)應(yīng)的。而樸素貝葉斯分類器是基于獨(dú)立假設(shè)的，即假設(shè)樣本每個(gè)特征與其他特征都不相關(guān)。

樸素貝葉斯分類器依靠精確的自然概率模型，在有監(jiān)督學(xué)習(xí)的樣本集中能獲取得非常好的分類效果。在許多實(shí)際應(yīng)用中，樸素貝葉斯模型參數(shù)估計(jì)使用最大似然估計(jì)方法，換言之樸素貝葉斯模型能工作并沒(méi)有用到貝葉斯概率或者任何貝葉斯模型。

審核編輯 ：李倩