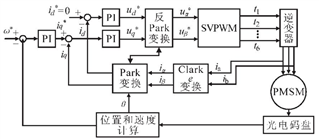
SVPWM,即空間矢量脈寬調制,由于在相同直流母線電壓下的電壓利用率比SPWM(正弦脈寬調制)高約15%,因而被廣泛應用于電機伺服驅動以及變頻器等場合。然而,傳統的SVPWM算法實現需要判斷矢量的扇區位置并計算矢量作用時間,求解過程設計較多浮點、三角函數與除法等運算,這對于低成本的微控制器而言,其運算難度較大。因此,設計一種運算簡單,易于微機實現的改進SVPWM算法具有重要意義。典型的電機矢量控制框圖如下:
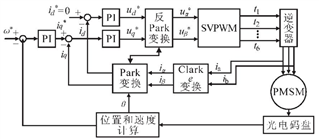
圖1 矢量控制框圖
可見SVPWM部分的目的就是把輸入的 , 轉換成六個開關管的導通時間,對應電機需要的ABC三相繞組電壓。通過數字方式實現矢量控制時,往往以占空比(實際為微機中用于產生PWM的比較值)代替實際電壓值。因此,在實現SVPWM時,僅需處理相應的坐標變換即可。
按電機繞組為星形連接為例,傳統SVPWM按照8種開關狀態進行分區,是基于六扇區進行矢量的分解與計算的,實際上(110,101,011)均可由(100,010,001)兩兩合成,即可簡化為三扇區。如下圖所示:
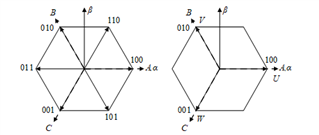
圖2 六扇區與三扇區
為與電機相軸區分,將(100,010,001)三電壓矢量方向分別稱為U、V和W軸。由于 , 是比較值形式的,將其坐標變換至UVW軸后將直接是每相上橋臂的占空比(比較值)。由于平面矢量合成僅需兩個線性無關的基本矢量,因此只需在UVW三軸中任意選擇兩個作為一個基,這里選取UV兩軸。
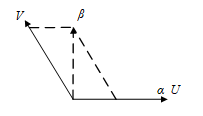
圖3 矢量分解圖
αβ軸到UV軸的矢量分解圖如上圖所示,其滿足平行四邊形法則,由圖有
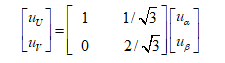 (1)
(1)
根據UV軸坐標的正負與大小關系,可將平面分為三個扇區,如圖3所示,圖中“+”號表示值為正數,“-”號則表示值為負數,在W軸線上有U=V。
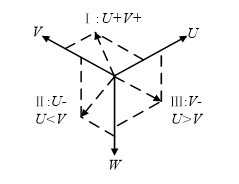
圖4 扇區劃分
前面提到,UVW軸坐標將直接是每相上橋臂的占空比(比較值),而在實際微機中比較值不能是負數,因此當UV中坐標出現負值時,可通過軸間對稱性等效轉換為另外兩軸的正坐標。以SVPWM的五段法為例,即零矢量全部為000矢量,其三相占空比(比較值)TA、TB與TC表達式如表3-2所示。
表1 各扇區占空比算式
|
Ⅰ |
Ⅱ |
Ⅲ |
|
TA= uU TB= uV TC= 0 |
TA= 0 TB= uV-uU TC= -uU |
TA= uU-uV TB= 0 TC= -uV |
五段法中零矢量全部選取為000,而若要實現七段法,需要替換一半時間的零矢量為111,則只需進一步通過下式修改即可。
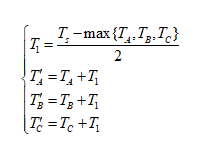
(2)
式中Ts為微機定時器周期值。可見,改進后的SVPWM算法只由乘加法與條件語句組成(小數使用Q格式運算),大大減小了運算難度,易于微機實現。
為驗證改進SVPWM算法的正確性,基于MATLAB/SIMULINK環境進行仿真,算法利用M語言通過S-Function實現。為便于對比,三相占空比(比較值)與線電壓均作歸一化處理,結果如圖4所示。
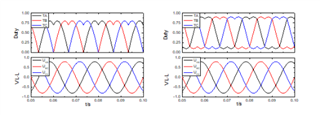
圖5五段法仿真結果(左)與七段法仿真結果(右)
同時在TI C2000系列微控制器TMS320F28027上進行實物代碼驗證,下圖為采用五段法時上橋臂AB兩相的調制波形,調制波形是經過RC低通濾波的,以去除高頻斬波分量,該調制波形為典型馬鞍波,與仿真結果相符。利用IO電平翻轉指示運算時間,在60MHz主頻的F28027上(Flash運行)三扇區快速SVPWM算法(第一段高電平)只需消耗8.9us,而傳統六扇區算法(第二段高電平)需要16us,可見三扇區算法可減小約44%執行時間并且代碼也更為簡潔(如附錄)。
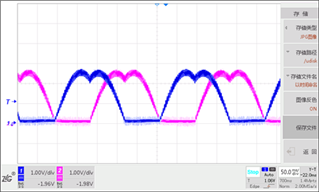
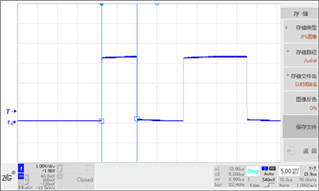
圖6五段法實驗結果(左)與算法消耗時間(右)
通過仿真與實驗結果可見,本文提到的基于三扇區的快速SVPWM在原理上以及實際實現上都是可行的,同時簡化的運算易于微機實現,適合應用在諸如各類經濟型變頻器等對微處理器成本敏感的場合。
五段法關鍵參考代碼:
|
三扇區快速SVPWM |
傳統六扇區SVPWM(已優化浮點與三角運算) |
|
//uA,uB分別為UV軸電壓,18918為Q15下的1/square(3),37836為Q15下的2/square(3) uA=u_alpha+((18918*u_beta)>>15); uB= ((37836*u_beta)>>15);
//TA,TB,TC為三相上橋臂比較器值 if((uA>=0)&&(uB>=0)) { TA=uA; TB=uB; TC=0; }
if((uA<=0)&&(uA<=uB)) { TA=0; TB=uB-uA; TC=-uA; }
if((uB<=0)&&(uB<=uA)) { TA=uA-uB; TB=0; TC=-uB; }
|
//18918為Q15下的1/square(3),37836為Q15下的2/square(3),56754 is Q15下的 square(3) X= u_beta; Y= 56754*u_alpha-u_beta; Z= -56754*u_alpha-u_beta;
if(X>=0) { if(Y>0) { Sector=1; } else if(Y<=0) { if(Z<0) { Sector=2; } else if(Z>=0) { Sector=3; } } } else if(X<0) { if(Y<=0) { Sector=4; } else if(Y>0) { if(Z>=0) { Sector=5; } else if(Z<0) { Sector=6; } } }
switch(Sector) { case 1: U4= u_alpha-((18918*u_beta)>>15); U6= ((37836*u_beta)>>15); TA=U4+U6; TB=U6; TC=0; break; case 2: U6= u_alpha+((18918*u_beta)>>15); U2= -u_alpha+((18918*u_beta)>>15); TA=U6; TB=U2+U6; TC=0; break; case 3: U2= ((37836*u_beta)>>15); U3= -u_alpha-((18918*u_beta)>>15); TA=0; TB=U2+U3; TC=U3; break; case 4: U3= -u_alpha+((18918*u_beta)>>15); U1= -((37836*u_beta)>>15); TA=0; TB=U3; TC=U1+U3; break; case 5: U1= -u_alpha-((18918*u_beta)>>15); U5= u_alpha-((18918*u_beta)>>15); TA=U5; TB=0; TC=U1+U5; break; case 6: U5= -((37836*u_beta)>>15); U4= u_alpha +((18918*u_beta)>>15); TA=U5+U4; TB=0; TC=U5; break; } |
-
控制器
+關注
關注
112文章
16214瀏覽量
177480 -
SVPWM
+關注
關注
14文章
614瀏覽量
90583 -
矢量控制
+關注
關注
2文章
284瀏覽量
32180
發布評論請先 登錄
相關推薦
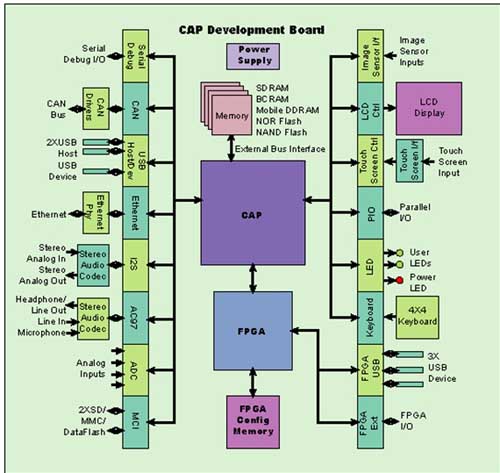
利用可定制微控制器優化算法設計
基于ARM9微控制器怎么實現上層控制算法?
采用FPGA來實現SVPWM調制算法
SVPWM算法在低成本微控制器中的實現方法
采用可定制微控制器來優化算法的設計
SVPWM算法在低成本微控制器中的快速實現
在高容量STM32F103xx微控制器中實現ADPCM算法





 微控制器中SVPWM算法的實現
微控制器中SVPWM算法的實現










評論