一、前言
計算機最喜歡的數(shù)字就是 0 和 1,在 CPU 的世界中,它只認識這兩個數(shù)字,即使是強大的操作系統(tǒng),也都是由 0 和 1 組成的。
作為一名軟件開發(fā)者,入門學(xué)習(xí)的內(nèi)容可能就是認識這 2 個既簡單、又強大的數(shù)字。但是大部分人,對于二進制、二進制計算、原碼、反碼以及補碼的認識,仍處于機械的強制記憶階段。尤其是對一些編碼和計算,仍然處于模糊的認識階段,例如:
CPU 是如何表示負數(shù)的?
為什么補碼可以用來表示負數(shù)?
一個 8 位的二進制數(shù),最小值為什么是 -128,而不是 -127?
CPU 中的加法器,為什么可以連同符號位一起運算?
這篇文章我們就來聊聊這個最最基礎(chǔ)的內(nèi)容,幫助你來理解二進制計算的相關(guān)內(nèi)容,看完這篇文章之后,不僅知其然,更能知其所以然!
PS: 這里有點高調(diào)了,最終的所以然部分,應(yīng)該涉及到數(shù)學(xué)證明這一層次了,本文并不會涉及到求證過程。
二、從十進制到二進制
1. 十進制
作為數(shù)學(xué)計算能力強大的中國,10 以內(nèi)的加減法,應(yīng)該是在幼兒園階段就完成了。如果你不屬于這個范圍,說明你上的是假幼兒園。
我們來快速復(fù)習(xí)一下關(guān)于十進制運算的一些基本知識:
每一個數(shù)位上包括的數(shù)字為 0 到 9;
每一個數(shù)位上的數(shù),是它右側(cè)數(shù)位的 10 倍;
兩個數(shù)相加時,相同數(shù)位上的數(shù)相加之和如果大于等于 10,就向前進 1 位,即:滿十進一;
具體來看就是:
從右數(shù)第一個位數(shù)(個位)上的數(shù)字代表多少個 1;
從右數(shù)第二個位數(shù)(十位)上的數(shù)字代表多少個 10;
從右數(shù)第三個位數(shù)(百位)上的數(shù)字代表多少個 100;
從右數(shù)第四個位數(shù)(千位)上的數(shù)字代表多少個 1000;
十進制的數(shù),可以使用后綴字母 D 來表示,也可以省略。例如:十進制的 1234 這個數(shù)字,個位上的數(shù)是 4, 十位上的數(shù)是 3, 百位上的數(shù)是 2,千位上的數(shù)是 1(一般是從最右側(cè)的個位說起),每一個數(shù)位上的數(shù)比它右側(cè)大十倍。如下圖:
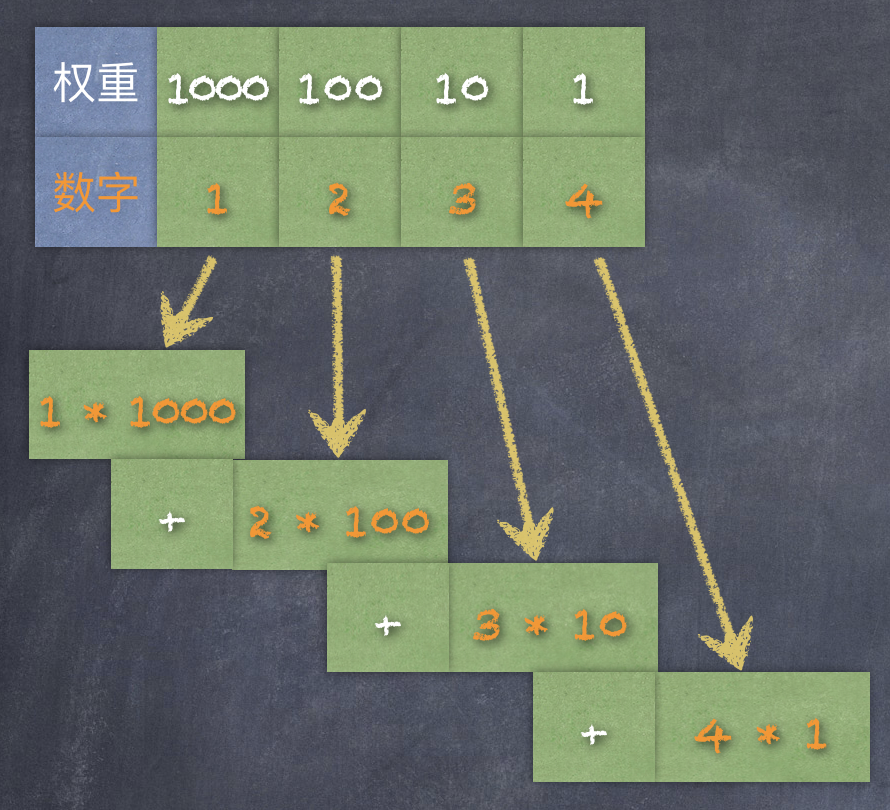
十進制數(shù)據(jù),也稱作基于十的表示法。
2. 二進制
那么對于二進制呢?直接套用上面十進制的概念,然后把 10 換成 2 即可(目前先忽略符號位):
每一個數(shù)位上包括的數(shù)字為 0 和 1;
每一個數(shù)位上的數(shù),是它右側(cè)數(shù)位的 2 倍;
兩個數(shù)相加時,相同數(shù)位上的數(shù)相加之和如果大于等于 2,就向前進 1 位,即:滿二進一;
具體來看就是:
從右數(shù)第一個位數(shù)上的數(shù)字代表多少個 1;
從右數(shù)第二個位數(shù)上的數(shù)字代表多少個 2;
從右數(shù)第三個位數(shù)上的數(shù)字代表多少個 4;
從右數(shù)第四個位數(shù)上的數(shù)字代表多少個 8;
記住幾個重點:二進制數(shù)中只包含 0 和 1 兩個數(shù)字,在相加時滿二進一。
在十進制中,每一個數(shù)位我們給它進行了專門的命名(個位、十位、百位...),但是二進制沒有類似的命名。
二進制的數(shù),使用后綴字母 B 來表示,例如:二進制的 1111B 這個數(shù)字,用圖來表示權(quán)重如下:
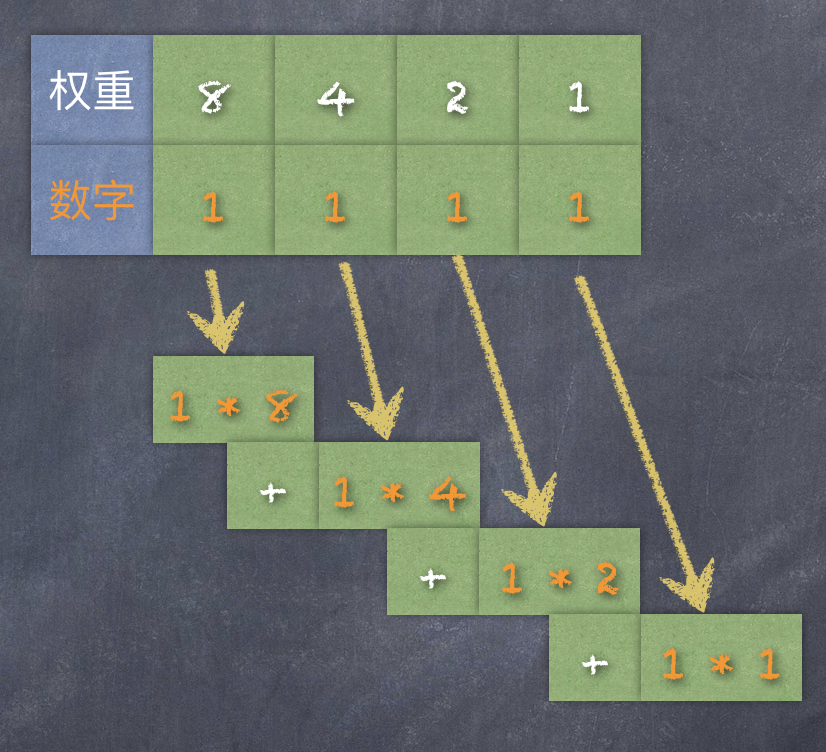
換算成十進制數(shù)就是 15(1 * 8 + 1 * 4 + 1 * 2 + 1 * 1 = 15)。
在二進制中,每一位稱為一個比特(bit),如果用 8 個 bit 來表示一個二進制數(shù),最小值是 0000_00000,最大值是 1111_1111;
如果用 16 個 bit 來表示一個二進制數(shù),最小值是 0000_0000_0000_0000,最大值是 1111_1111_1111_1111。(為了便于觀察,每 4 個 bit 之間,加上了分隔符)
在早期的計算機中,8 位的處理器很常見,于是就給它一個專門的名字:字節(jié)(Byte)。16 位的二進制數(shù)就是 2 個字節(jié),也稱作:字(Word)。
3. 擴展到十六進制
原理還是相同的:直接把十進制中的 10 換成 16 即可:
每一個數(shù)位上包括的數(shù)字為 0 到 9,A 到 F;
每一個數(shù)位上的數(shù),是它右側(cè)數(shù)位的 16 倍;
兩個數(shù)相加時,相同數(shù)位上的數(shù)相加之和如果大于等于 16,就向前進 1 位,即:滿十六進一;
具體來看就是:
從右數(shù)第一個位數(shù)上的數(shù)字代表多少個 1;
從右數(shù)第二個位數(shù)上的數(shù)字代表多少個 16;
從右數(shù)第三個位數(shù)上的數(shù)字代表多少個 256;
從右數(shù)第四個位數(shù)上的數(shù)字代表多少個 4096;
在十六進制中,需要十六個數(shù)字來表示 0 到 15 這些數(shù)字,0 到 9 比較好處理,但是從 10 到 15,我們就需要找一些記號來表示,于是人們就想到用 A,B,C,D,E,F 這幾個字母來分別表示 10 到 15 這個 6 個數(shù)字。
十六進制數(shù)據(jù),使用后綴字母 H 來表示,有些場合也可以使用前綴 0x 來表示,本質(zhì)上沒有區(qū)別。例如:十六進制數(shù)字 1A2BH(或者寫作 0x1A2B),每一個數(shù)位上的權(quán)重如圖:
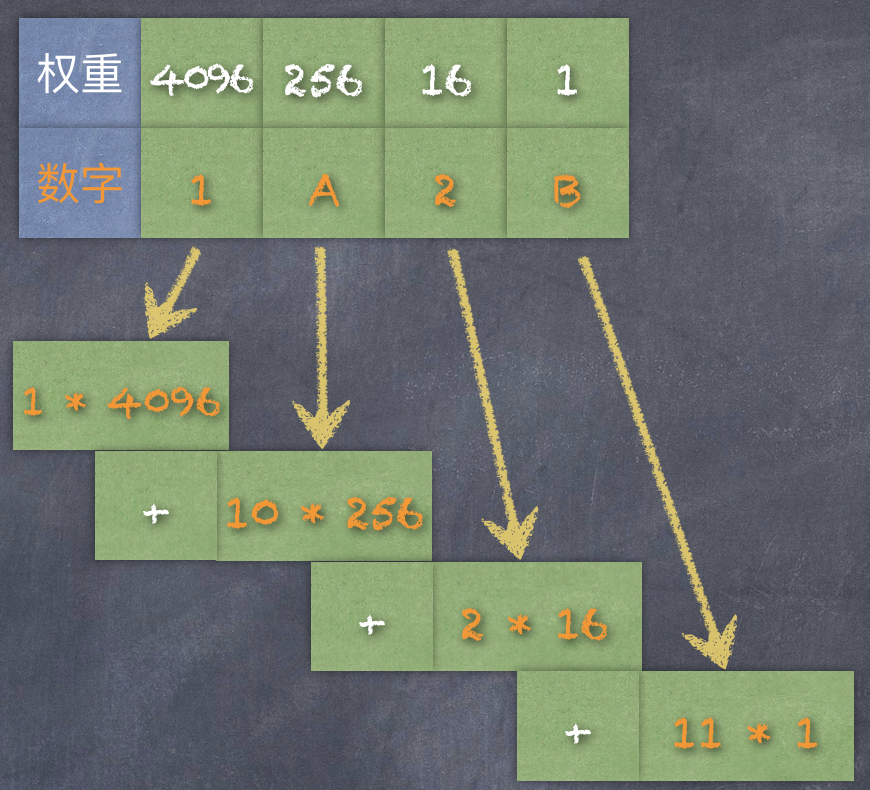
換算成十進制數(shù)就是 6699(1 * 4096 + 10 * 256 + 2 * 16 + 11 * 1 = 6699)。
4. 擴展到任意進制
原理仍然相同:直接把十進制中的 10 換成目標進制,例如 5 進制:
每一個數(shù)位上包括的數(shù)字為 0 到 4;
每一個數(shù)位上的數(shù),是它右側(cè)數(shù)位的 5 倍;
兩個數(shù)相加時,相同數(shù)位上的數(shù)相加之和如果大于等于 5,就向前進 1 位,即:滿五進一;
具體來看就是:
從右數(shù)第一個位數(shù)上的數(shù)字代表多少個 1;
從右數(shù)第二個位數(shù)上的數(shù)字代表多少個 5;
從右數(shù)第三個位數(shù)上的數(shù)字代表多少個 25;
從右數(shù)第四個位數(shù)上的數(shù)字代表多少個 125;
再看一個圖加深印象:
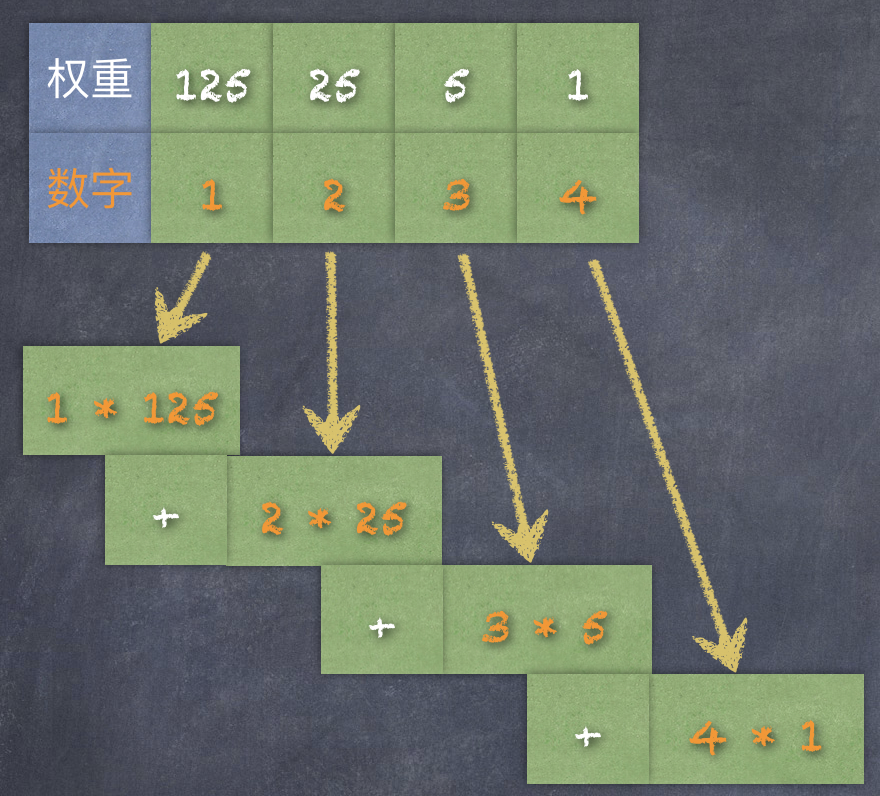
三、從十進制加法到二進制加法
1. 十進制加法
這個就不必多說了,規(guī)則只有 2 條:
兩個數(shù),相同數(shù)位上的數(shù)字進行相加;
每一個數(shù)位上的相加結(jié)果,滿十進一;
例如:
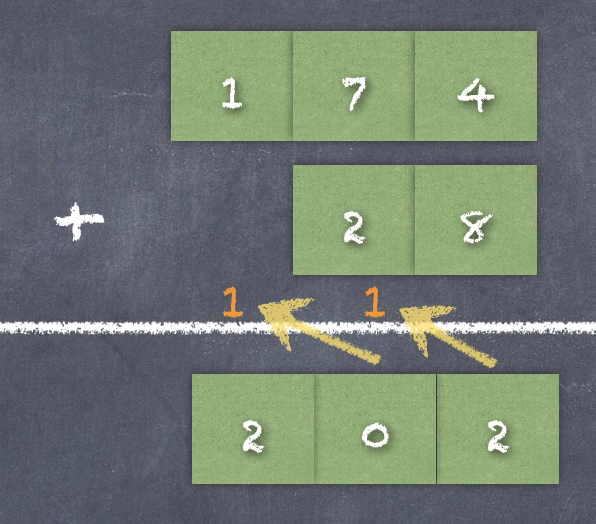
個位上:4 + 8,結(jié)果是 12,但是十進制中沒有 12 這個數(shù)字,因此向左側(cè)的高位進1,個位就剩下:12 - 10 = 2。
十位上:7 + 2,再加上進位 1,結(jié)果是 10,但是十進制中沒有 10 這個數(shù)字,因此向左側(cè)的高位進1,十位變成:10 - 10 = 0。
百位上:1 加上進位 1,結(jié)果是 2。
2. 二進制加法
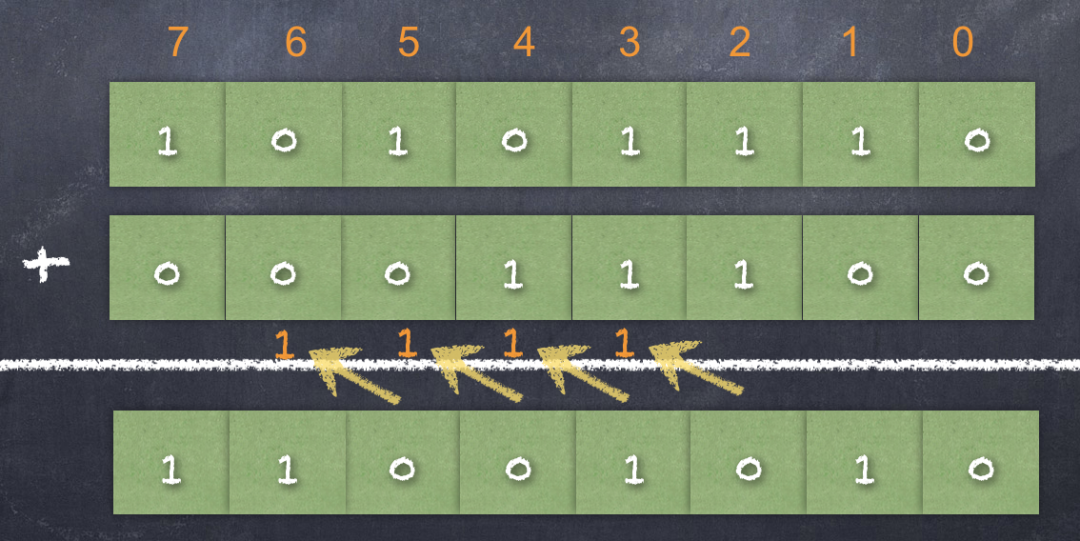
第 0 位:0 + 0 結(jié)果為 0;
第 1 位:1 + 0 結(jié)果為 1;
第 2 位:1 + 1 結(jié)果為 2,但是二進制中沒有 2 這個數(shù)字,因此需要向左側(cè)的高位進 1,于是第 2 位上就剩下 2 - 2 = 0。
第 3 位:1 + 1 等于 2,再加上進位 1,結(jié)果就是 3,但是二進制中沒有 3 這個數(shù)字,因此需要向左側(cè)的高位進 1,于是第 3 位上就剩下 3 - 2 = 1。
第 4,5,6,7位計算均是如此。
3. 十六進制加法
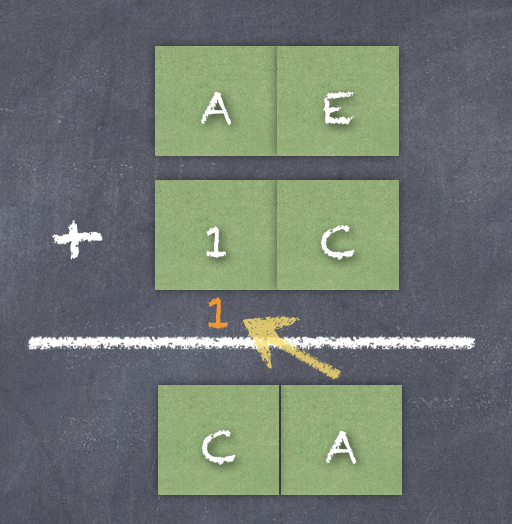
第 0 位:E + C,結(jié)果為 26,但是十六進制中沒有 26 這個數(shù)字,因此需要向左側(cè)的高位進 1,于是第 0 位就剩下 26 - 16 = A。
第 1 位:A + 1 等于 B,再加上進位 1,結(jié)果就是 C,十六機制中有這個數(shù)字。
四、把負數(shù)計算轉(zhuǎn)換成正數(shù)計算
1. 原碼
原碼(true form)是一種計算機中對數(shù)字的二進制定點表示方法。原碼表示法在數(shù)值前面增加了一位符號位(即最高位為符號位):正數(shù)該位為0,負數(shù)該位為1(0有兩種表示:+0和-0),其余位表示數(shù)值的大小。
例如,用 8 個 bit (8 位二進制數(shù))來表示一個數(shù),+11 的原碼為 0000_1011,-11 的原碼就是 1000_1011。
2. 把負數(shù)計算變成正數(shù)計算
我們都知道,CPU 中有加法器,好像從來沒有聽說過“減法器”。例如計算 5 + 8,轉(zhuǎn)換成二進制來計算:

再來計算一下減法:5 - 8,對于 CPU 來說,只會計算 5 + 8, 但是不會計算 5 - 8。
但是可以轉(zhuǎn)換一下思路,把減法變成加法 5 + (-8),這樣不就可以計算了嗎?于是計算機先驅(qū)者就發(fā)明了反碼:
正數(shù)的反碼:保持原碼不變;
負數(shù)的反碼:原碼中符號位不變,其余全部取反(-8 的原碼是 1000_1000,反碼就是:1111_0111);
于是 5 + (-8)的計算過程就是:

此時,就完美解決了減法問題,那么乘法(多加幾次)、除法(多減幾次)問題也就跟著解決了。至于如何從數(shù)學(xué)的角度來證明,那就要問那些數(shù)學(xué)家了!
3. 新問題:如何表示0?
我們現(xiàn)在可以小結(jié)一下反碼的表示范圍(記住:第一位是符號位):
正數(shù)的表示范圍:0000_0000 ~ 0111_1111,也就是十進制的 +0 ~ +127 這 128 個數(shù);
負數(shù)的表示范圍:1000_0000 ~ 1111_1111,也就是十進制的 -127 ~ -0 這 128 個數(shù);
有沒有發(fā)現(xiàn)問題:怎么存在 +0 和 -0 這兩個數(shù)?而且他們的編碼還不一樣:+0 對應(yīng) 0000_0000,-0 對應(yīng) 1111_1111。
CPU 雖然就是一個傻瓜,讓它干啥就干啥,但是 CPU 最不能容忍的就是不確定性!我們都知道 +0 == -0 == 0,它們是同一個數(shù)字,但是在二進制編碼中,居然有兩個編碼來表示同一個數(shù)。
偉大的計算機先驅(qū)者又做了這樣一個決定:正數(shù)保持不變,負數(shù)整體減 1。
也就是說:符號位不變,值整體加1,如下:
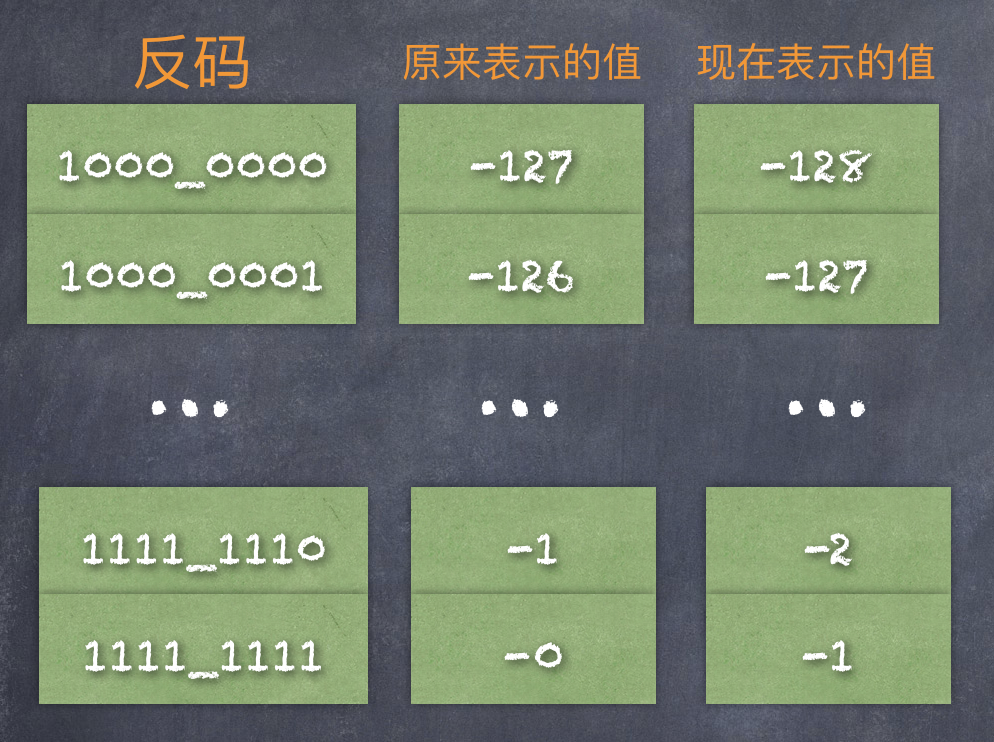
這樣就成功解決了 -0、+0 的問題!
現(xiàn)在 一個 8 位的二進制就可以表示的范圍是:-128 ~ 127,并且中間沒有任何重復(fù)、遺漏的數(shù)字。
既然每一個二進制表示的值發(fā)生了變化,那么繼續(xù)稱之為反碼就不準確了,此時給它們一個新的稱呼:補碼,也就是說:上圖就變成了這樣:
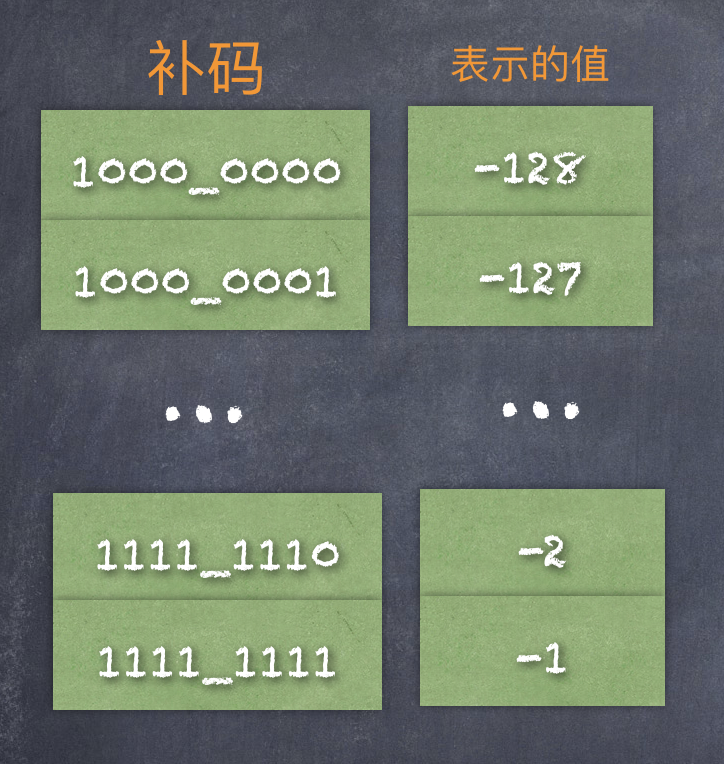
小結(jié)一下補碼的定義:
正數(shù)的補碼:保持原碼不變;
負數(shù)的補碼:原碼中符號位不變,其余先全部取反,然后再加1(例如:-8 的原碼是 1000_1000,補碼就是 1111_1000);
此時,我們僅僅是解決了二級制編碼的表示問題,那么:補碼能直接參與運算嗎?運算結(jié)果會出現(xiàn)什么問題?
4. 補碼的計算
我們先看一下這個問題:假設(shè)現(xiàn)在時間是 1 點整,但是你的手表進水了,它顯示的是 3 點整,現(xiàn)在你怎么把時間調(diào)整到 1 點的位置?
方法1:把時針逆時針撥動 2 個小時(3 - 2 = 1);
方法2:把時針順時針撥動 9 個小時到 12 點,然后再撥動 1 個小時(3 + 10 = 1);
對于時鐘表盤來說,每 12 個小時為一圈,可以認為:-2 == 10,-1 = 11, -3 = 9,同樣的:-2 == 10, -2 == 22, -2 == 34,...
可以看到規(guī)律是:-2、10、22、34 這些數(shù)字對 12 取模都得到同一個數(shù)(取正數(shù)),在數(shù)學(xué)上,兩個整數(shù)除以“同一個整數(shù)”,若得相同余數(shù),則這兩個整數(shù)同余。
表盤中的 12 就是這個“同一個整數(shù)”,可以看到這是一個可“溢出”的系統(tǒng),-2、10、22、34 這幾個數(shù)在表盤上表示的是一樣的數(shù),所以說這幾個整數(shù)同余。
也就是說:在計算的時候,可以用 10、22、34 這幾個數(shù)字來替換 -2,替換之后的計算結(jié)果是相同的。
那么對于一個 8 位 的二進制數(shù)來說,最多只有 8 位,在計算過程中,如果最高位產(chǎn)生了進位,就會被丟棄,所以它也是一個可“溢出”的系統(tǒng)。那么這里的“同一個整數(shù)”是多少呢?
從前面的內(nèi)容中可以看到,使用補碼表示的 8 位二進制數(shù)表示的范圍是 -128 ~ 127,一共是 256 個數(shù),所以如果對 256 取模,得到相同的余數(shù),那么這些數(shù)就是同余數(shù)。
例如:-2 和 254 對 256 取模,得到相同的余數(shù),因此它倆就是同余數(shù),那么在計算的時候,就可以用 254 來代替 -2。
那么我們通過計算 3 + (-2) 來驗證一下。
(1) 利用同余數(shù)來計算
3 + (-2) == 3 + 254 = 257
257 超過了最大的表示范圍,所以溢出,結(jié)果就是 257 對 256 取模,結(jié)果為 1。
(2) 直接用補碼來計算
3 的補碼是 0000_0011,-2 的補碼是 1111_1110,在計算的時候,把符號位也參與運算:

結(jié)果也是 1,也就是說:
在二進制計算中,使用補碼來計算,“天然”就滿足了“同余定理”。
細心的讀者可能已經(jīng)發(fā)現(xiàn)了:-2 的二進制補碼表示,與 254 的二進制自然表示,它們的形式是一樣的!
這種“天然”性,是巧合?還是計算機前輩的設(shè)計結(jié)果?!
五、總結(jié)
這篇文章,我們探討了計算機系統(tǒng)的軟件基石:二進制系統(tǒng),主要的目的是幫助你理解二進制的表示、計算方式。
希望你看完之后能夠豁然開朗!如果對您的理解有幫助的話,請轉(zhuǎn)發(fā)給身邊的技術(shù)小伙伴,共同成長!
謝謝!
審核編輯 :李倩
-
cpu
+關(guān)注
關(guān)注
68文章
10829瀏覽量
211194 -
二進制
+關(guān)注
關(guān)注
2文章
794瀏覽量
41603 -
計算機系統(tǒng)
+關(guān)注
關(guān)注
0文章
281瀏覽量
24089
原文標題:關(guān)于二進制表示和補碼計算的來龍去脈,入門看了秒懂
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
hex格式和二進制的區(qū)別
為什么Gain=1對應(yīng)的默認值不是16位二進制補碼的中間數(shù)而是最小數(shù)?
ASCII碼和二進制的轉(zhuǎn)換關(guān)系
二進制編碼器工作原理 如何選擇二進制編碼器
二進制補碼及與原碼的互相轉(zhuǎn)換方法
計算機采用二進制的原因不包括什么
二進制處理中的一些技巧
二進制串行計數(shù)器工作原理是什么?
如何實現(xiàn)二進制和BCD碼數(shù)據(jù)的相互轉(zhuǎn)變?
二進制與邏輯電平的變化范圍





 關(guān)于二進制表示和補碼計算
關(guān)于二進制表示和補碼計算










評論