文章從實際出發,講述了什么是傅里葉變換,它的理論基礎以及Numpy和OpenCV實現傅里葉和逆傅里葉變換,并最終用高通濾波和低通濾波的示例。
1. 什么是傅里葉變換及其基礎理論
1.1傅里葉變換
圖像處理一般分為直接對圖像內的像素進行處理的空間域處理和頻率域處理。
空間域處理主要劃分為灰度變換和空間濾波兩種形式。
灰度變換是對圖像內的單個像素進行處理,比如調節對比度和處理閾值等。
空間濾波涉及圖像質量的改變,例如圖像平滑處理。空間域處理的計算簡單方便,運算速度更快。
頻率域處理是先將圖像變換到頻率域,然后在頻率域對圖像進行處理,最后再通過反變換將圖像從頻率域變換到空間域。
1.2基礎理論
時間差,在傅里葉變換里就是相位。相位表述的是與時間差相關的信息。
在圖像處理過程中,傅里葉變換就是將圖像分解為正弦分量和余弦分量兩部分,即將圖像從空間域轉換到頻域。
數字圖像經過傅里葉變換后,得到的頻域值是復數。因此,顯示傅里葉變換的結果需要使用實數圖像(real image)加虛數圖像(complex image),或者幅度圖像(magnitude image)加相位圖像(phase image)的形式。因為幅度圖像包含了原圖像中我們所需要的大部分信息,所以在圖像處理過程中,通常僅使用幅度圖像。
如果希望先在頻域內對圖像進行處理,再通過逆傅里葉變換得到修改后的空域圖像,就必須同時保留幅度圖像和相位圖像。對圖像進行傅里葉變換后,會得到圖像中的低頻和高頻信息。低頻信息對應圖像內變化緩慢的灰度分量。高頻信息對應圖像內變化越來越快的灰度分量,是由灰度的尖銳過渡造成的。
傅里葉變換的目的,就是為了將圖像從空域轉換到頻域,并在頻域內實現對圖像內特定對象的處理,然后再對經過處理的頻域圖像進行逆傅里葉變換得到空域圖像。
2. Numpy實現傅里葉和逆傅里葉變換
2.1Numpy實現傅里葉變換
Numpy模塊中的fft2()函數可以實現圖像的傅里葉變換。
Numpy提供的實現傅里葉變換的函數是numpy.fft.fft2(),它的語法格式是:
返回值 = numpy.fft.fft2(原始圖像)
參數“原始圖像”的類型是灰度圖像,函數的返回值是一個復數數組(complex ndarray)。經過該函數的處理,就能得到圖像的頻譜信息。此時,圖像頻譜中的零頻率分量位于頻譜圖像(頻域圖像)的左上角。
為了便于觀察,通常會使用numpy.fft.fftshift()函數將零頻率成分移動到頻域圖像的中心位置。函數numpy.fft.fftshift()的語法格式是:
返回值=numpy.fft.fftshift(原始頻譜)
為了顯示為圖像,需要將它們的值調整到[0, 255]的灰度空間內,使用的公式為:
像素新值=20*np.log(np.abs(頻譜值))
用Numpy實現傅里葉變換,觀察得到的頻譜圖像。
import cv2import numpy as npimport matplotlib.pyplot as pltimg=cv2.imread('./img/hand1.png',0)f = np.fft.fft2(img)fshift = np.fft.fftshift(f)magnitude_spectrum = 20*np.log(np.abs(fshift))plt.subplot(121)plt.imshow(img, cmap = 'gray')plt.title('original')plt.axis('off')plt.subplot(122)plt.imshow(magnitude_spectrum, cmap = 'gray')plt.title('result')plt.axis('off')plt.show()
2.2 實現逆傅里葉變換
注意: 如果在傅里葉變換過程中使用了numpy.fft.fftshift()函數移動零頻率分量,那么在逆傅里葉變換過程中,需要先使用numpy.fft.ifftshift()函數將零頻率分量移到原來的位置,再進行逆傅里葉變換
函數numpy.fft.ifftshift()是numpy.fft.fftshift()的逆函數,其語法格式為:
調整后的頻譜 = numpy.fft.ifftshift(原始頻譜)
numpy.fft.ifft2()函數可以實現逆傅里葉變換,返回空域復數數組。
它是numpy.fft.fft2()的逆函數,該函數的語法格式為:
返回值=numpy.fft.ifft2(頻域數據)
函數numpy.fft.ifft2()的返回值仍舊是一個復數數組(complex ndarray)。
逆傅里葉變換得到的空域信息是一個復數數組,需要將該信息調整至[0, 255]灰度空間內,使用的公式為:
iimg = np.abs(逆傅里葉變換結果)
在Numpy內實現傅里葉變換、逆傅里葉變換,觀察逆傅里葉變換的結果圖像。
import cv2import numpy as npimport matplotlib.pyplot as pltimg = cv2.imread('./img/hand1.png',0)f = np.fft.fft2(img)fshift = np.fft.fftshift(f)ishift = np.fft.ifftshift(fshift)iimg = np.fft.ifft2(ishift)iimg = np.abs(iimg)plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iimg, cmap = 'gray')plt.title('iimg'), plt.axis('off')plt.show()
2.3高通濾波示例
一幅圖像內,同時存在著高頻信號和低頻信號。
低頻信號對應圖像內變化緩慢的灰度分量。例如,在一幅大草原的圖像中,低頻信號對應著顏色趨于一致的廣袤草原。高頻信號對應圖像內變化越來越快的灰度分量,是由灰度的尖銳過渡造成的。如果在上面的大草原圖像中還有一頭獅子,那么高頻信號就對應著獅子的邊緣等信息。
濾波器能夠允許一定頻率的分量通過或者拒絕其通過,按照其作用方式可以劃分為低通濾波器和高通濾波器。
允許低頻信號通過的濾波器稱為低通濾波器。低通濾波器使高頻信號衰減而對低頻信號放行,會使圖像變模糊。允許高頻信號通過的濾波器稱為高通濾波器。高通濾波器使低頻信號衰減而讓高頻信號通過,將增強圖像中尖銳的細節,但是會導致圖像的對比度降低。
傅里葉變換可以將圖像的高頻信號和低頻信號分離。通過對圖像的頻域處理,可以實現圖像增強、圖像去噪、邊緣檢測、特征提取、壓縮和加密等操作。
在Numpy內對圖像進行傅里葉變換,得到其頻域圖像。然后,在頻域內將低頻分量的值處理為0,實現高通濾波。最后,對圖像進行逆傅里葉變換,得到恢復的原始圖像。
import cv2import numpy as npimport matplotlib.pyplot as pltimg = cv2.imread('./img/hand1.png',0)f = np.fft.fft2(img)fshift = np.fft.fftshift(f)rows, cols = img.shapecrow, ccol = int(rows/2) , int(cols/2)fshift[crow-30:crow+30, ccol-30:ccol+30] = 0ishift = np.fft.ifftshift(fshift)iimg = np.fft.ifft2(ishift)iimg = np.abs(iimg)plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iimg, cmap = 'gray')plt.title('iimg'), plt.axis('off')plt.show()
3.OpenCV實現傅里葉和逆傅里葉變換及低通濾波示例
3.1 OpenCV實現傅里葉變換
OpenCV提供了函數cv2.dft()和cv2.idft()來實現傅里葉變換和逆傅里葉變換
函數cv2.dft()的語法格式為:
返回結果=cv2.dft(原始圖像,轉換標識)
在使用該函數時,需要注意參數的使用規范:對于參數“原始圖像”,要首先使用np.float32()函數將圖像轉換成np.float32格式。“轉換標識”的值通常為“cv2.DFT_COMPLEX_OUTPUT”,用來輸出一個復數陣列。
函數cv2.dft()返回的結果與使用Numpy進行傅里葉變換得到的結果是一致的,但是它返回的值是雙通道的,第1個通道是結果的實數部分,第2個通道是結果的虛數部分。
經過函數cv2.dft()的變換后,得到了原始圖像的頻譜信息。此時,零頻率分量并不在中心位置,為了處理方便需要將其移至中心位置,可以用函數numpy.fft.fftshift()實現。
例如,如下語句將頻譜圖像dft中的零頻率分量移到頻譜中心,得到了零頻率分量位于中心的頻譜圖像dftshift。
dftShift = np.fft.fftshift(dft)
經過上述處理后,頻譜圖像還只是一個由實部和虛部構成的值。要將其顯示出來,還要做進一步的處理才行。
函數cv2.magnitude()可以計算頻譜信息的幅度。該函數的語法格式為:
返回值=cv2.magnitude(參數1,參數2)
參數1:浮點型x坐標值,也就是實部。參數2:浮點型y坐標值,也就是虛部,它必須和參數1具有相同的size
函數cv2.magnitude()的返回值是參數1和參數2的平方和的平方根,公式為:
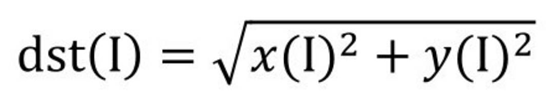
得到頻譜信息的幅度后,通常還要對幅度值做進一步的轉換,以便將頻譜信息以圖像的形式展示出來。簡單來說,就是需要將幅度值映射到灰度圖像的灰度空間[0, 255]內,使其以灰度圖像的形式顯示出來。
這里使用的公式為:
result = 20*np.log(cv2.magnitude(實部,虛部))
用OpenCV函數對圖像進行傅里葉變換,并展示其頻譜信息。import numpy as npimport cv2img = cv2.imread('./img/hand1.png',0)dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)print(dft)dftShift = np.fft.fftshift(dft)print(dftShift)result = 20*np.log(cv2.magnitude(dftShift[:, :,0], dftShift[:, :,1])) #兩個參數,需要拆分通道print(result)
import numpy as npimport cv2import matplotlib.pyplot as pltimg=cv2.imread('./img/hand1.png',0)dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)dftShift = np.fft.fftshift(dft)result = 20*np.log(cv2.magnitude(dftShift[:, :,0], dftShift[:, :,1]))plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(result, cmap = 'gray')plt.title('result'), plt.axis('off')plt.show()
3.2實現逆傅里葉變換
在OpenCV中,使用函數cv2.idft()實現逆傅里葉變換,該函數是傅里葉變換函數cv2.dft()的逆函數。其語法格式為:
返回結果=cv2.idft(原始數據)
對圖像進行傅里葉變換后,通常會將零頻率分量移至頻譜圖像的中心位置。如果使用函數numpy.fft.fftshift()移動了零頻率分量,那么在進行逆傅里葉變換前,要使用函數numpy.fft.ifftshift()將零頻率分量恢復到原來位置。
注意: 在進行逆傅里葉變換后,得到的值仍舊是復數,需要使用函數cv2.magnitude()計算其幅度。
用OpenCV函數對圖像進行傅里葉變換、逆傅里葉變換,并展示原始圖像及經過逆傅里葉變換后得到的圖像。
import numpy as npimport cv2import matplotlib.pyplot as pltimg=cv2.imread('./img/hand1.png',0)dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)dftShift = np.fft.fftshift(dft)ishift=np.fft.ifftshift(dftShift)iImg = cv2.idft(ishift)iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1]) # 計算幅度plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iImg, cmap = 'gray')plt.title('inverse'), plt.axis('off')plt.show()
3.3低通濾波示例
在一幅圖像內,低頻信號對應圖像內變化緩慢的灰度分量。圖像進行低通濾波后會變模糊

實現的中間步驟
rows, cols = img.shape crow, ccol = int(rows/2) , int(cols/2) mask = np.zeros((rows, cols,2), np.uint8) # 二維的原因,有實部和虛部 mask[crow-30:crow+30, ccol-30:ccol+30,:] = 1
然后,將其與頻譜圖像進行運算,實現低通濾波。這里采用的運算形式是:
fShift = dftShift*mask
使用函數cv2.dft()對圖像進行傅里葉變換,得到其頻譜圖像。然后,在頻域內將其高頻分量的值處理為0,實現低通濾波。最后,對圖像進行逆傅里葉變換,得到恢復的原始圖像。
經過低通濾波后,圖像的邊緣信息被削弱了。import numpy as npimport cv2import matplotlib.pyplot as pltimg = cv2.imread('./img/hand1.png',0)dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)dftShift = np.fft.fftshift(dft)rows, cols = img.shapecrow, ccol = int(rows/2) , int(cols/2)mask = np.zeros((rows, cols,2), np.uint8)#兩個通道,與頻域圖像匹配mask[crow-30:crow+30, ccol-30:ccol+30,:] = 1fShift = dftShift*maskishift = np.fft.ifftshift(fShift)iImg = cv2.idft(ishift)iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1])plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iImg, cmap = 'gray')plt.title('inverse'), plt.axis('off')plt.show()
審核編輯:郭婷
-
濾波
+關注
關注
10文章
663瀏覽量
56603 -
頻率
+關注
關注
4文章
1459瀏覽量
59163
原文標題:圖像處理:使用Numpy和OpenCV實現傅里葉和逆傅里葉變換
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
傅里葉變換的基本性質和定理
經典傅里葉變換與快速傅里葉變換的區別
如何實現離散傅里葉變換
傅里葉變換與圖像處理技術的區別
傅里葉變換在信號處理中的應用
傅里葉變換的數學原理
傅里葉變換紅外光譜儀技術在光伏材料性能表征中的應用與優化





 使用Numpy和OpenCV實現傅里葉和逆傅里葉變換
使用Numpy和OpenCV實現傅里葉和逆傅里葉變換











評論