140.單詞拆分II（困難）

之前手把手帶你刷二叉樹(shù)（綱領(lǐng)篇）把遞歸窮舉劃分為「遍歷」和「分解問(wèn)題」兩種思路，其中「遍歷」的思路擴(kuò)展延伸一下就是回溯算法，「分解問(wèn)題」的思路可以擴(kuò)展成動(dòng)態(tài)規(guī)劃算法。

我在手把手帶你刷二叉樹(shù)（思路篇）對(duì)一些二叉樹(shù)問(wèn)題進(jìn)行舉例，同時(shí)給出「遍歷」和「分解問(wèn)題」兩種思路的解法，幫大家借助二叉樹(shù)理解更高級(jí)的算法設(shè)計(jì)思想。

當(dāng)然，這種思維轉(zhuǎn)換不止局限于二叉樹(shù)相關(guān)的算法，本文就跳出二叉樹(shù)類型問(wèn)題，來(lái)看看實(shí)際算法題中如何把問(wèn)題抽象成樹(shù)形結(jié)構(gòu)，從而進(jìn)行「遍歷」和「分解問(wèn)題」的思維轉(zhuǎn)換，從回溯算法順滑地切換到動(dòng)態(tài)規(guī)劃算法。

先說(shuō)句題外話，前文動(dòng)態(tài)規(guī)劃核心框架詳解說(shuō)，標(biāo)準(zhǔn)的動(dòng)態(tài)規(guī)劃問(wèn)題一定是求最值的，因?yàn)閯?dòng)態(tài)規(guī)劃類型問(wèn)題有一個(gè)性質(zhì)叫做「最優(yōu)子結(jié)構(gòu)」，即從子問(wèn)題的最優(yōu)解推導(dǎo)出原問(wèn)題的最優(yōu)解。

但在我們平常的語(yǔ)境中，就算不是求最值的題目，只要看見(jiàn)使用備忘錄消除重疊子問(wèn)題，我們一般都稱它為動(dòng)態(tài)規(guī)劃算法。嚴(yán)格來(lái)講這是不符合動(dòng)態(tài)規(guī)劃問(wèn)題的定義的，說(shuō)這種解法叫做「帶備忘錄的 DFS 算法」可能更準(zhǔn)確些。不過(guò)咱也不用太糾結(jié)這種名詞層面的細(xì)節(jié)，既然大家叫的順口，就叫它動(dòng)態(tài)規(guī)劃也無(wú)妨。

本文講解的兩道題目也不是求最值的，但依然會(huì)把他們的解法稱為動(dòng)態(tài)規(guī)劃解法，這里提前跟大家說(shuō)下這里面的細(xì)節(jié)，免得細(xì)心的讀者疑惑。其他不多說(shuō)了，直接看題目吧。

單詞拆分 I

首先看下力扣第 139 題「單詞拆分」：

函數(shù)簽名如下：

booleanwordBreak(Strings,ListwordDict);

這是一道非常高頻的面試題，我們來(lái)思考下如何通過(guò)「遍歷」和「分解問(wèn)題」的思路來(lái)解決它。

先說(shuō)說(shuō)「遍歷」的思路，也就是用回溯算法解決本題。回溯算法最經(jīng)典的應(yīng)用就是排列組合相關(guān)的問(wèn)題了，不難發(fā)現(xiàn)這道題換個(gè)說(shuō)法也可以變成一個(gè)排列問(wèn)題：

現(xiàn)在給你一個(gè)不包含重復(fù)單詞的單詞列表wordDict和一個(gè)字符串s，請(qǐng)你判斷是否可以從wordDict中選出若干單詞的排列（可以重復(fù)挑選）構(gòu)成字符串s。

這就是前文回溯算法秒殺排列組合問(wèn)題的九種變體中講到的最后一種變體：元素?zé)o重可復(fù)選的排列問(wèn)題，前文我寫了一個(gè)permuteRepeat函數(shù)，代碼如下：

List>res=newLinkedList<>();
LinkedListtrack=newLinkedList<>();

//元素?zé)o重可復(fù)選的全排列
publicList>permuteRepeat(int[]nums){
backtrack(nums);
returnres;
}

//回溯算法核心函數(shù)
voidbacktrack(int[]nums){
//basecase，到達(dá)葉子節(jié)點(diǎn)
if(track.size()==nums.length){
//收集根到葉子節(jié)點(diǎn)路徑上的值
res.add(newLinkedList(track));
return;
}

//回溯算法標(biāo)準(zhǔn)框架
for(inti=0;i//做選擇
track.add(nums[i]);
//進(jìn)入下一層回溯樹(shù)
backtrack(nums);
//取消選擇
track.removeLast();
}
}

給這個(gè)函數(shù)輸入nums = [1,2,3]，輸出是 3^3 = 27 種可能的組合：

[
[1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],
[2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],
[3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
]

這段代碼實(shí)際上就是遍歷一棵高度為N + 1的滿N叉樹(shù)（N為nums的長(zhǎng)度），其中根到葉子的每條路徑上的元素就是一個(gè)排列結(jié)果：

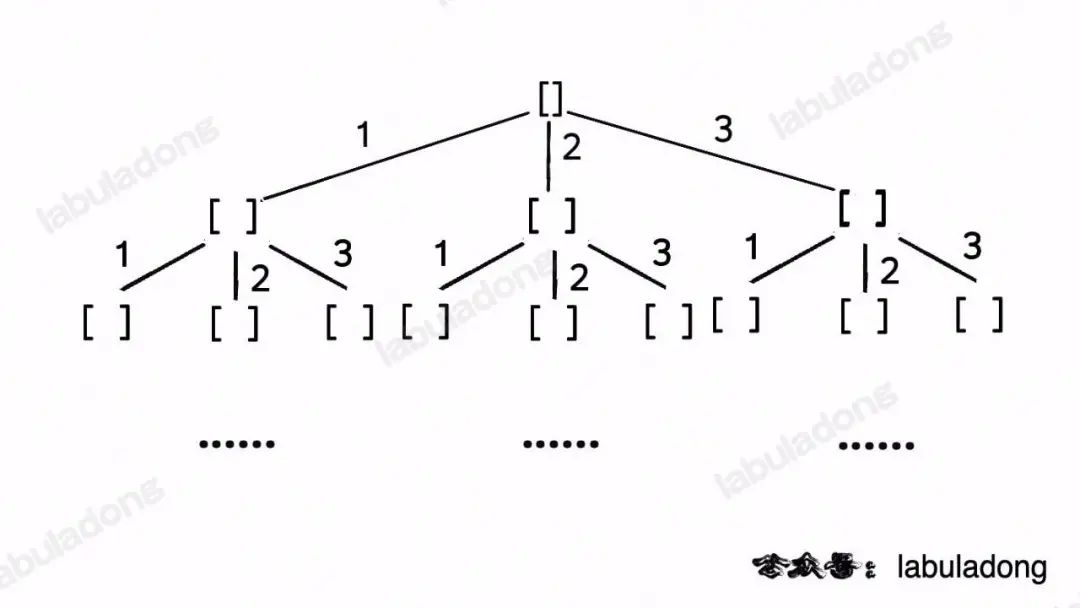
類比一下，本文講的這道題也有異曲同工之妙，假設(shè)wordDict = ["a", "aa", "ab"], s = "aaab"，想用wordDict中的單詞拼出s，其實(shí)也面對(duì)著類似的一棵M叉樹(shù)，M為wordDict中單詞的個(gè)數(shù)，你需要做的就是站在回溯樹(shù)的每個(gè)節(jié)點(diǎn)上，看看哪個(gè)單詞能夠匹配s[i..]的前綴，從而判斷應(yīng)該往哪條樹(shù)枝上走：

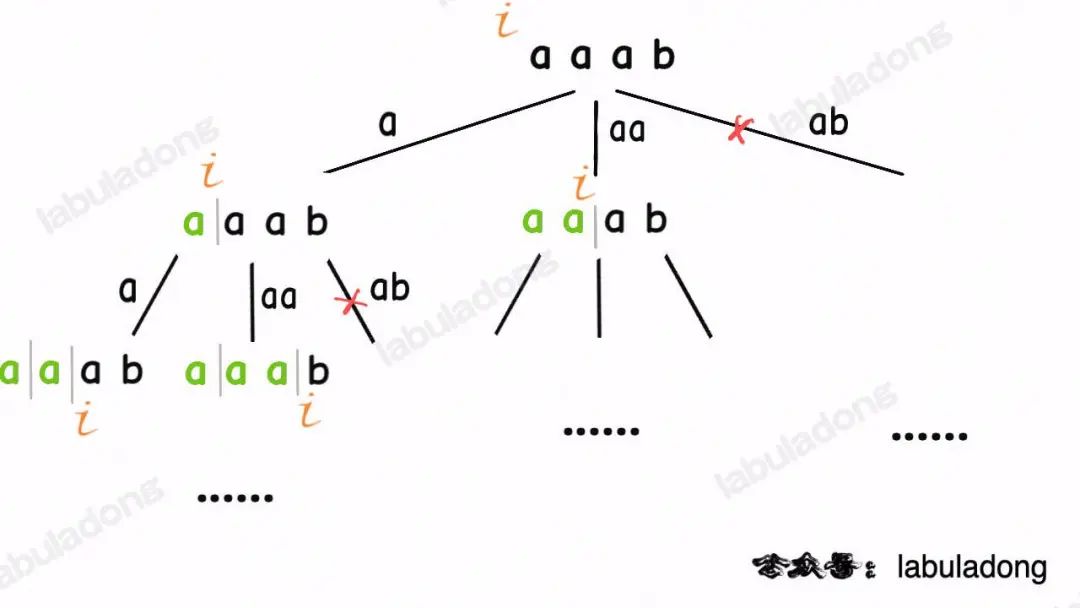
然后，按照前文回溯算法框架詳解所說(shuō)，你把backtrack函數(shù)理解成在回溯樹(shù)上游走的一個(gè)指針，維護(hù)每個(gè)節(jié)點(diǎn)上的變量i，即可遍歷整棵回溯樹(shù)，尋找出匹配s的組合。

回溯算法解法代碼如下：

ListwordDict;
//記錄是否找到一個(gè)合法的答案
booleanfound=false;
//記錄回溯算法的路徑
LinkedListtrack=newLinkedList<>();

//主函數(shù)
publicbooleanwordBreak(Strings,ListwordDict){
this.wordDict=wordDict;
//執(zhí)行回溯算法窮舉所有可能的組合
backtrack(s,0);
returnfound;
}

//回溯算法框架
voidbacktrack(Strings,inti){
//basecase
if(found){
//如果已經(jīng)找到答案，就不要再遞歸搜索了
return;
}
if(i==s.length()){
//整個(gè)s都被匹配完成，找到一個(gè)合法答案
found=true;
return;
}

//回溯算法框架
for(Stringword:wordDict){
//看看哪個(gè)單詞能夠匹配s[i..]的前綴
intlen=word.length();
if(i+len<=?s.length()
????????????&&?s.substring(i,?i?+?len).equals(word))?{
????????????//找到一個(gè)單詞匹配s[i..i+len)
//做選擇
track.addLast(word);
//進(jìn)入回溯樹(shù)的下一層，繼續(xù)匹配s[i+len..]
backtrack(s,i+len);
//撤銷選擇
track.removeLast();
}
}
}

這段代碼就是嚴(yán)格按照回溯算法框架寫出來(lái)的，應(yīng)該不難理解，但這段代碼無(wú)法通過(guò)所有測(cè)試用例，我們按照之前算法時(shí)空復(fù)雜度使用指南中講到的方法來(lái)分析一下它的時(shí)間復(fù)雜度。

遞歸函數(shù)的時(shí)間復(fù)雜度的粗略估算方法就是用遞歸函數(shù)調(diào)用次數(shù)（遞歸樹(shù)的節(jié)點(diǎn)數(shù)） x 遞歸函數(shù)本身的復(fù)雜度。對(duì)于這道題來(lái)說(shuō)，遞歸樹(shù)的每個(gè)節(jié)點(diǎn)其實(shí)就是對(duì)s進(jìn)行的一次切割，那么最壞情況下s能有多少種切割呢？

長(zhǎng)度為N的字符串s中共有N - 1個(gè)「縫隙」可供切割，每個(gè)縫隙可以選擇「切」或者「不切」，所以s最多有O(2^N)種切割方式，即遞歸樹(shù)上最多有O(2^N)個(gè)節(jié)點(diǎn)。

當(dāng)然，實(shí)際情況可定會(huì)好一些，畢竟存在剪枝邏輯，但從最壞復(fù)雜度的角度來(lái)看，遞歸樹(shù)的節(jié)點(diǎn)個(gè)數(shù)確實(shí)是指數(shù)級(jí)別的。

那么backtrack函數(shù)本身的時(shí)間復(fù)雜度是多少呢？主要的時(shí)間消耗是遍歷wordDict尋找匹配s[i..]的前綴的單詞：

//遍歷wordDict的所有單詞
for(Stringword:wordDict){
//看看哪個(gè)單詞能夠匹配s[i..]的前綴
intlen=word.length();
if(i+len<=?s.length()
????????&&?s.substring(i,?i?+?len).equals(word))?{
????????//找到一個(gè)單詞匹配s[i..i+len)
//...
}
}

設(shè)wordDict的長(zhǎng)度為M，字符串s的長(zhǎng)度為N，那么這段代碼的最壞時(shí)間復(fù)雜度是O(MN)（for 循環(huán)O(M)，Java 的substring方法O(N)），所以總的時(shí)間復(fù)雜度是O(2^N * MN)。

這里順便說(shuō)一個(gè)細(xì)節(jié)優(yōu)化，其實(shí)你也可以反過(guò)來(lái)，通過(guò)窮舉s[i..]的前綴去判斷wordDict中是否有對(duì)應(yīng)的單詞：

//注意，要轉(zhuǎn)化成哈希集合，提高contains方法的效率
HashSetwordDict=newHashSet<>(wordDict);

//遍歷s[i..]的所有前綴
for(intlen=1;i+len<=?s.length();?len++)?{
????//看看wordDict中是否有單詞能匹配s[i..]的前綴
Stringprefix=s.substring(i,i+len);
if(wordDict.contains(prefix)){
//找到一個(gè)單詞匹配s[i..i+len)
//...
}
}

這段代碼和剛才那段代碼的結(jié)果是一樣的，但這段代碼的時(shí)間復(fù)雜度變成了O(N^2)，和剛才的代碼不同。

到底哪樣子好呢？這要看題目給的數(shù)據(jù)范圍。本題說(shuō)了1 <= s.length <= 300, 1 <= wordDict.length <= 1000，所以O(N^2)的結(jié)果較小，這段代碼的實(shí)際運(yùn)行效率應(yīng)該稍微高一些，這個(gè)是一個(gè)細(xì)節(jié)的優(yōu)化，你可以自己做一下，我就不寫了。

不過(guò)即便你優(yōu)化這段代碼，總的時(shí)間復(fù)雜度依然是指數(shù)級(jí)的O(2^N * N^2)，是無(wú)法通過(guò)所有測(cè)試用例的，那么問(wèn)題出在哪里呢？

比如輸入wordDict = ["a", "aa"], s = "aaab"，算法無(wú)法找到一個(gè)可行的組合，所以一定會(huì)遍歷整棵回溯樹(shù)，但你注意這里面會(huì)存在重復(fù)的情況：

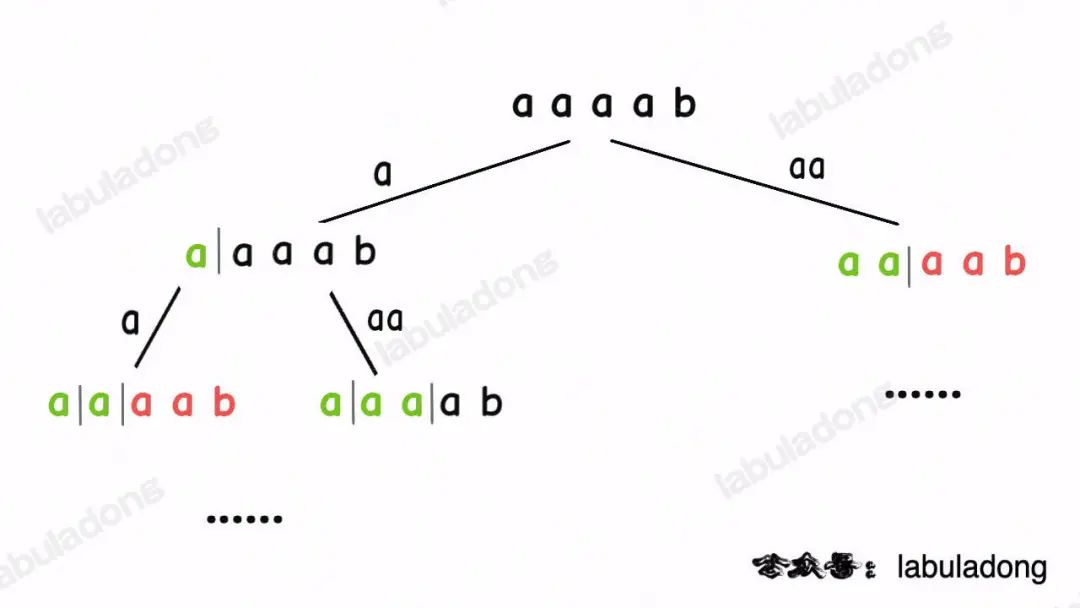
圖中標(biāo)紅的這兩部分，雖然經(jīng)歷了不同的切分，但是切分得出的結(jié)果是相同的，所以這兩個(gè)節(jié)點(diǎn)下面的子樹(shù)也是重復(fù)的，即存在冗余計(jì)算，極端情況下會(huì)消耗大量時(shí)間。

如何消除冗余計(jì)算呢？這就要稍微轉(zhuǎn)變一下思維模式，用「分解問(wèn)題」的思維模式來(lái)考慮這道題。

我們剛才以排列組合的視角思考這個(gè)問(wèn)題，現(xiàn)在我們換一種視角，思考一下是否能夠把原問(wèn)題分解成規(guī)模更小，結(jié)構(gòu)相同的子問(wèn)題，然后通過(guò)子問(wèn)題的結(jié)果計(jì)算原問(wèn)題的結(jié)果。

對(duì)于輸入的字符串s，如果我能夠從單詞列表wordDict中找到一個(gè)單詞匹配s的前綴s[0..k]，那么只要我能拼出s[k+1..]，就一定能拼出整個(gè)s。

換句話說(shuō)，我把規(guī)模較大的原問(wèn)題wordBreak(s[0..])分解成了規(guī)模較小的子問(wèn)題wordBreak(s[k+1..])，然后通過(guò)子問(wèn)題的解反推出原問(wèn)題的解。

有了這個(gè)思路就可以定義一個(gè)dp函數(shù)，并給出該函數(shù)的定義：

//定義：返回 s[i..]是否能夠被拼出
intdp(Strings,inti);

//計(jì)算整個(gè)s是否能被拼出，調(diào)用dp(s,0)

有了這個(gè)函數(shù)定義，就可以把剛才的邏輯大致翻譯成偽碼：

ListwordDict;

//定義：返回 s[i..]是否能夠被拼出
intdp(Strings,inti){
//basecase，s[i..]是空串
if(i==s.length()){
returntrue;
}
//遍歷wordDict，
//看看哪些單詞是s[i..]的前綴
for(Strnigword:wordDict){
ifword是s[i..]的前綴{
intlen=word.length();
//只要s[i+len..]可以被拼出，
//s[i..]就能被拼出
if(dp(s,i+len)==true){
returntrue;
}
}
}
//所有單詞都嘗試過(guò)，無(wú)法拼出整個(gè)s
returnfalse;
}

類似之前講的回溯算法，dp函數(shù)中的 for 循環(huán)也可以優(yōu)化一下：

//注意，用哈希集合快速判斷元素是否存在
HashSetwordDict;

//定義：返回 s[i..]是否能夠被拼出
intdp(Strings,inti){
//basecase，s[i..]是空串
if(i==s.length()){
returntrue;
}

//遍歷s[i..]的所有前綴，
//看看哪些前綴存在wordDict中
for(intlen=1;i+len<=?s.length();?len++)?{
ifwordDict中存在s[i..len){
//只要s[i+len..]可以被拼出，
//s[i..]就能被拼出
if(dp(s,i+len)==true){
returntrue;
}
}
}
//所有單詞都嘗試過(guò)，無(wú)法拼出整個(gè)s
returnfalse;
}

對(duì)于這個(gè)dp函數(shù)，指針i的位置就是「狀態(tài)」，所以我們可以通過(guò)添加備忘錄的方式優(yōu)化效率，避免對(duì)相同的子問(wèn)題進(jìn)行冗余計(jì)算。最終的解法代碼如下：

//用哈希集合方便快速判斷是否存在
HashSetwordDict;
//備忘錄，-1代表未計(jì)算，0代表無(wú)法湊出，1代表可以湊出
int[]memo;

//主函數(shù)
publicbooleanwordBreak(Strings,ListwordDict){
//轉(zhuǎn)化為哈希集合，快速判斷元素是否存在
this.wordDict=newHashSet<>(wordDict);
//備忘錄初始化為-1
this.memo=newint[s.length()];
Arrays.fill(memo,-1);
returndp(s,0);
}

//定義：s[i..]是否能夠被拼出
booleandp(Strings,inti){
//basecase
if(i==s.length()){
returntrue;
}
//防止冗余計(jì)算
if(memo[i]!=-1){
returnmemo[i]==0?false:true;
}

//遍歷s[i..]的所有前綴
for(intlen=1;i+len<=?s.length();?len++)?{
????????//看看哪些前綴存在wordDict中
Stringprefix=s.substring(i,i+len);
if(wordDict.contains(prefix)){
//找到一個(gè)單詞匹配s[i..i+len)
//只要s[i+len..]可以被拼出，s[i..]就能被拼出
booleansubProblem=dp(s,i+len);
if(subProblem==true){
memo[i]=1;
returntrue;
}
}
}
//s[i..]無(wú)法被拼出
memo[i]=0;
returnfalse;
}

這個(gè)解法能夠通過(guò)所有測(cè)試用例，我們根據(jù)算法時(shí)空復(fù)雜度使用指南來(lái)算一下它的時(shí)間復(fù)雜度：

因?yàn)橛袀渫浀妮o助，消除了遞歸樹(shù)上的重復(fù)節(jié)點(diǎn)，使得遞歸函數(shù)的調(diào)用次數(shù)從指數(shù)級(jí)別降低為狀態(tài)的個(gè)數(shù)O(N)，函數(shù)本身的復(fù)雜度還是O(N^2)，所以總的時(shí)間復(fù)雜度是O(N^3)，相較回溯算法的效率有大幅提升。

單詞拆分 II

有了上一道題的鋪墊，力扣第 140 題「單詞拆分 II」就容易多了，先看下題目：

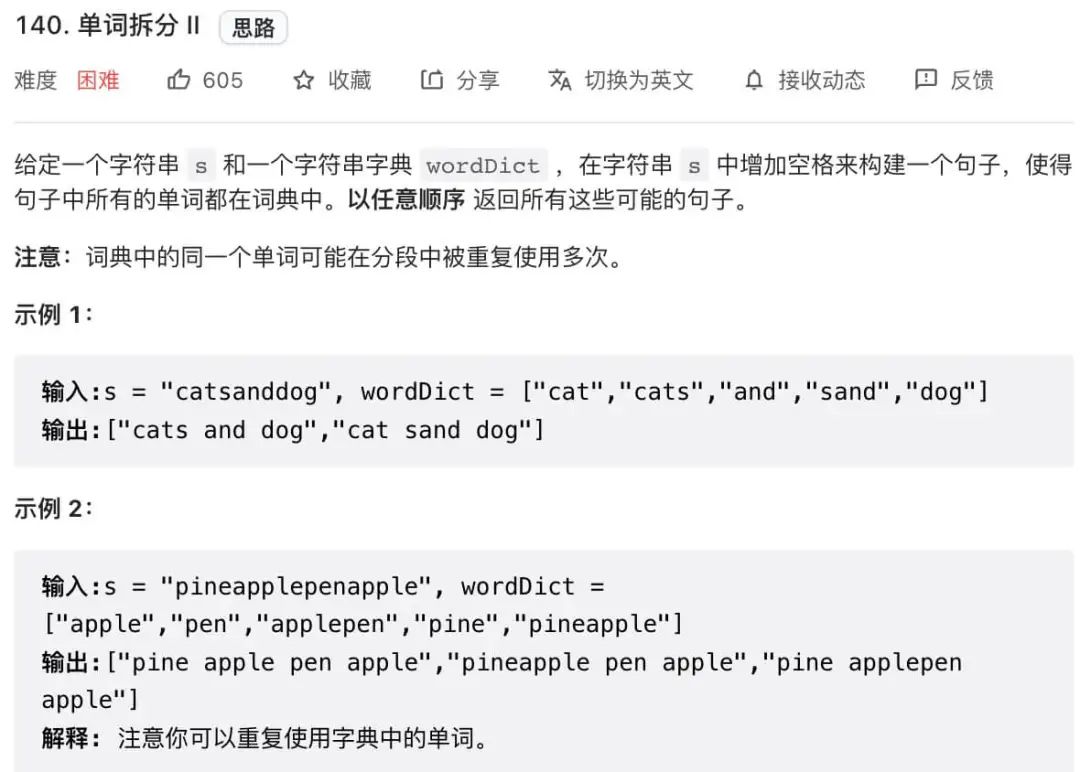
相較上一題，這道題不是單單問(wèn)你s是否能被拼出，還要問(wèn)你是怎么拼的，其實(shí)只要把之前的解法稍微改一改就可以解決這道題。

上一道題的回溯算法維護(hù)一個(gè)found變量，只要找到一種拼接方案就提前結(jié)束遍歷回溯樹(shù)，那么在這道題中我們不要提前結(jié)束遍歷，并把所有可行的拼接方案收集起來(lái)就能得到答案：

//記錄結(jié)果
Listres=newLinkedList<>();
//記錄回溯算法的路徑
LinkedListtrack=newLinkedList<>();
ListwordDict;

//主函數(shù)
publicListwordBreak(Strings,ListwordDict){
this.wordDict=wordDict;
//執(zhí)行回溯算法窮舉所有可能的組合
backtrack(s,0);
returnres;
}

//回溯算法框架
voidbacktrack(Strings,inti){
//basecase
if(i==s.length()){
//找到一個(gè)合法組合拼出整個(gè)s，轉(zhuǎn)化成字符串
res.add(String.join("",track));
return;
}

//回溯算法框架
for(Stringword:wordDict){
//看看哪個(gè)單詞能夠匹配s[i..]的前綴
intlen=word.length();
if(i+len<=?s.length()
????????????&&?s.substring(i,?i?+?len).equals(word))?{
????????????//找到一個(gè)單詞匹配s[i..i+len)
//做選擇
track.addLast(word);
//進(jìn)入回溯樹(shù)的下一層，繼續(xù)匹配s[i+len..]
backtrack(s,i+len);
//撤銷選擇
track.removeLast();
}
}
}

這個(gè)解法的時(shí)間復(fù)雜度和前一道題類似，依然是O(2^N * MN)，但由于這道題給的數(shù)據(jù)規(guī)模較小，所以可以通過(guò)所有測(cè)試用例。

類似的，這個(gè)問(wèn)題也可以用分解問(wèn)題的思維解決，把上一道題的dp函數(shù)稍作修改即可：

HashSetwordDict;
//備忘錄
List[]memo;

publicListwordBreak(Strings,ListwordDict){
this.wordDict=newHashSet<>(wordDict);
memo=newList[s.length()];
returndp(s,0);
}



//定義：返回用 wordDict 構(gòu)成 s[i..]的所有可能
Listdp(Strings,inti){
Listres=newLinkedList<>();
if(i==s.length()){
res.add("");
returnres;
}
//防止冗余計(jì)算
if(memo[i]!=null){
returnmemo[i];
}

//遍歷s[i..]的所有前綴
for(intlen=1;i+len<=?s.length();?len++)?{
????????//看看哪些前綴存在wordDict中
Stringprefix=s.substring(i,i+len);
if(wordDict.contains(prefix)){
//找到一個(gè)單詞匹配s[i..i+len)
ListsubProblem=dp(s,i+len);
//構(gòu)成s[i+len..]的所有組合加上prefix
//就是構(gòu)成構(gòu)成s[i]的所有組合
for(Stringsub:subProblem){
if(sub.isEmpty()){
//防止多余的空格
res.add(prefix);
}else{
res.add(prefix+""+sub);
}
}
}
}
//存入備忘錄
memo[i]=res;

returnres;
}

這個(gè)解法依然用備忘錄消除了重疊子問(wèn)題，所以dp函數(shù)遞歸調(diào)用的次數(shù)減少為O(N)，但dp函數(shù)本身的時(shí)間復(fù)雜度上升了，因?yàn)?/span>subProblem是一個(gè)子集列表，它的長(zhǎng)度是指數(shù)級(jí)的。

再加上 Java 中用+拼接字符串的效率并不高，且還要消耗備忘錄去存儲(chǔ)所有子問(wèn)題的結(jié)果，所以這個(gè)算法的時(shí)間復(fù)雜度并不比回溯算法低，依然是指數(shù)級(jí)別。

綜上，我們處理排列組合問(wèn)題時(shí)一般使用回溯算法去「遍歷」回溯樹(shù)，而不用「分解問(wèn)題」的思路去處理，因?yàn)榇鎯?chǔ)子問(wèn)題的結(jié)果就需要大量的時(shí)間和空間，除非重疊子問(wèn)題的數(shù)量較多的極端情況，否則得不償失。

以上就是本文的全部?jī)?nèi)容，希望你能對(duì)回溯思路和分解問(wèn)題的思路有更深刻的理解。

審核編輯 ：李倩