數(shù)據(jù)類別不均衡問題應該是一個極常見又頭疼的的問題了。最近在工作中也是碰到這個問題,花了些時間梳理并實踐了類別不均衡問題的解決方式,主要實踐了“魔改”loss(focal loss, GHM loss, dice loss 等),整理如下。
所有的 Loss 實踐代碼在這里:
https://github.com/shuxinyin/NLP-Loss-Pytorch
數(shù)據(jù)不均衡問題也可以說是一個長尾問題,但長尾那部分數(shù)據(jù)往往是重要且不能被忽略的,它不僅僅是分類標簽下樣本數(shù)量的不平衡,實質上也是難易樣本的不平衡。
解決不均衡問題一般從兩方面入手:
數(shù)據(jù)層面:重采樣,使得參與迭代計算的數(shù)據(jù)是均衡的;
模型層面:重加權,修改模型的 loss,在 loss 計算上,加大對少樣本的 loss 獎勵。
1. 數(shù)據(jù)層面的重采樣
關于數(shù)據(jù)層面的重采樣,方式都是通過采樣,重新構造數(shù)據(jù)分布,使得數(shù)據(jù)平衡。一般常用的有三種:
欠采樣;
過采樣;
SMOTE。
1. 欠采樣:指某類別下數(shù)據(jù)較多,則只采取部分數(shù)據(jù),直接拋棄一些數(shù)據(jù),這種方式太簡單粗暴,擬合出來的模型的偏差大,泛化性能較差;
2. 過采樣:這種方式與欠采樣相反,某類別下數(shù)據(jù)較少,進行重復采樣,達到數(shù)據(jù)平衡。因為這些少的數(shù)據(jù)反復迭代計算,會使得模型產(chǎn)生過擬合的現(xiàn)象。
3. SMOTE:一種近鄰插值,可以降低過擬合風險,但它是適用于回歸預測場景下,而 NLP 任務一般是離散的情況。
這幾種方法單獨使用會或多或少造成數(shù)據(jù)的浪費或重,一般會與 ensemble 方式結合使用,sample 多份數(shù)據(jù),訓練出多個模型,最后綜合。
但以上幾種方式在工程實踐中往往是少用的,一是因為數(shù)真實據(jù)珍貴,二也是 ensemble 的方式部署中資源消耗大,沒法接受。因此,就集中看下重加權 loss 改進的部分。
2. 模型層面的重加權
重加權主要指的是在 loss 計算階段,通過設計 loss,調整類別的權值對 loss 的貢獻。比較經(jīng)典的 loss 改進應該是 Focal Loss, GHM Loss, Dice Loss。
2.1 Focal Loss
Focal Loss 是一種解決不平衡問題的經(jīng)典 loss,基本思想就是把注意力集中于那些預測不準的樣本上。
何為預測不準的樣本?比如正樣本的預測值小于 0.5 的,或者負樣本的預測值大于 0.5 的樣本。再簡單點,就是當正樣本預測值》0.5 時,在計算該樣本的 loss 時,給它一個小的權值,反之,正樣本預測值《0.5 時,給它一個大的權值。同理,對負樣本時也是如此。
以二分類為例,一般采用交叉熵作為模型損失。

其中 是真實標簽, 是預測值,在此基礎又出來了一個權重交叉熵,即用一個超參去緩解上述這種影響,也就是下式。

接下來,看下 Focal Loss 是怎么做到集中關注預測不準的樣本?
在交叉熵 loss 基礎上,當正樣本預測值 大于 0.5 時,需要給它的 loss 一個小的權重值 ,使其對總 loss 影響小,反之正樣本預測值 小于 0.5,給它的 loss 一個大的權重值。為滿足以上要求,則 增大時, 應減小,故剛好 可滿足上述要求。
因此加上注意參數(shù) ,得到 Focal Loss 的二分類情況:
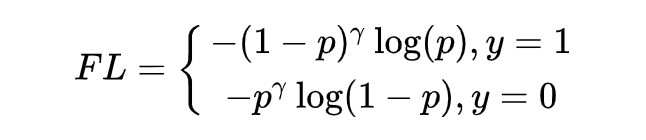
加上調節(jié)系數(shù) ,F(xiàn)ocal Loss 推廣到多分類的情況:
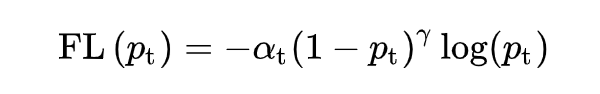
其中 為第 t 類預測值,,試驗中效果最佳時,。
代碼的實現(xiàn)也是比較簡潔的。
def __init__(self, num_class, alpha=None, gamma=2, reduction=‘mean’): super(MultiFocalLoss, self).__init__() self.gamma = gamma 。..。..
def forward(self, logit, target): alpha = self.alpha.to(logit.device) prob = F.softmax(logit, dim=1)
ori_shp = target.shape target = target.view(-1, 1)
prob = prob.gather(1, target).view(-1) + self.smooth # avoid nan logpt = torch.log(prob)
alpha_weight = alpha[target.squeeze().long()] loss = -alpha_weight * torch.pow(torch.sub(1.0, prob), self.gamma) * logpt
if self.reduction == ‘mean’: loss = loss.mean()
return loss
2.2 GHM Loss
上面的 Focal Loss 注重了對 hard example 的學習,但不是所有的 hard example 都值得關注,有一些 hard example 很可能是離群點,這種離群點當然是不應該讓模型關注的。
GHM (gradient harmonizing mechanism) 是一種梯度調和機制,GHM Loss 的改進思想有兩點:1)就是在使模型繼續(xù)保持對 hard example 關注的基礎上,使模型不去關注這些離群樣本;2)另外 Focal Loss 中, 的值分別由實驗經(jīng)驗得出,而一般情況下超參 是互相影響的,應當共同進行實驗得到。
Focal Loss 中通過調節(jié)置信度 ,當正樣本中模型的預測值 較小時,則乘上(1-p),給一個大的 loss 值使得模型關注這種樣本。于是 GHM Loss 在此基礎上,規(guī)定了一個置信度范圍 ,具體一點,就是當正樣本中模型的預測值為 較小時,要看這個 多小,若是 ,這種樣本可能就是離群點,就不注意它了。
于是 GHM Loss 首先規(guī)定了一個梯度模長 :
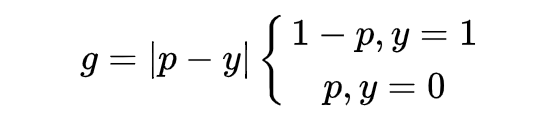
其中, 是模型預測概率值, 是 ground-truth 的標簽值,這里以二分類為例,取值為 0 或 1。可發(fā)現(xiàn), 表示檢測的難易程度, 越大則檢測難度越大。
GHM Loss 的思想是,不要關注那些容易學的樣本,也不要關注那些離群點特別難分的樣本。所以問題就轉為我們需要尋找一個變量去衡量這個樣本是不是這兩種,這個變量需滿足當 值大時,它要小,從而進行抑制,當 值小時,它也要小,進行抑制。于是文中就引入了梯度密度:
表明了樣本 1~N 中,梯度模長分布在 范圍內的樣本個數(shù), 代表了 區(qū)間的長度,因此梯度密度 GD(g) 的物理含義是:單位梯度模長 部分的樣本個數(shù)。
在此基礎上,還需要一個前提,那就是處于 值小與大的樣本(也就是易分樣本與難分樣本)的數(shù)量遠多于中間值樣本,此時 GD 才可以滿足上述變量的要求。

此時,對于每個樣本,把交叉熵 CE×該樣本梯度密度的倒數(shù),就得到 GHM Loss。

這里附上邏輯的代碼,完整的可以上文章首尾倉庫查看。
class GHM_Loss(nn.Module): def __init__(self, bins, alpha): super(GHM_Loss, self).__init__() self._bins = bins self._alpha = alpha self._last_bin_count = None
def _g2bin(self, g): # split to n bins return torch.floor(g * (self._bins - 0.0001)).long()
def forward(self, x, target): # compute value g g = torch.abs(self._custom_loss_grad(x, target)).detach()
bin_idx = self._g2bin(g)
bin_count = torch.zeros((self._bins)) for i in range(self._bins): # 計算落入bins的梯度模長數(shù)量 bin_count[i] = (bin_idx == i).sum().item()
N = (x.size(0) * x.size(1))
if self._last_bin_count is None: self._last_bin_count = bin_count else: bin_count = self._alpha * self._last_bin_count + (1 - self._alpha) * bin_count self._last_bin_count = bin_count
nonempty_bins = (bin_count 》 0).sum().item()
gd = bin_count * nonempty_bins gd = torch.clamp(gd, min=0.0001) beta = N / gd # 計算好樣本的gd值
# 借由binary_cross_entropy_with_logits,gd值當作參數(shù)傳入 return F.binary_cross_entropy_with_logits(x, target, weight=beta[bin_idx])
2.3 Dice Loss & DSC Loss
Dice Loss 是來自文章 V-Net 提出的,DSC Loss 是香儂科技的 Dice Loss for Data-imbalanced NLP Tasks。
按照上面的邏輯,看一下 Dice Loss 是怎么演變過來的。Dice Loss 主要來自于 dice coefficient,dice coefficient 是一種用于評估兩個樣本的相似性的度量函數(shù)。
定義是這樣的:取值范圍在 0 到 1 之間,值越大表示越相似。若令 X 是所有模型預測為正的樣本的集合,Y 為所有實際上為正類的樣本集合,dice coefficient 可重寫為:
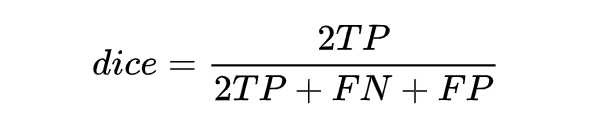
同時,結合 F1 的指標計算公式推一下,可得:
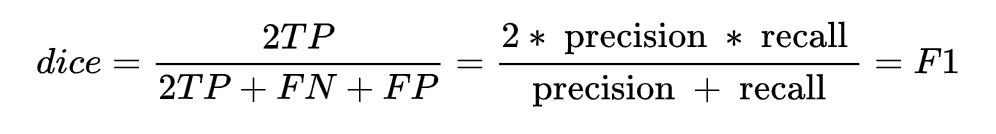
可以動手推一下,就能得到 dice coefficient 是等同 F1 score 的,因此本質上 dice loss 是直接優(yōu)化 F1 指標的。
上述表達式是離散的,需要把上述 DSC 表達式轉化為連續(xù)的版本,需要進行軟化處理。對單個樣本 x,可以直接定義它的 DSC:

但是當樣本為負樣本時,y1=0,loss 就為 0 了,需要加一個平滑項。

上面有說到 dice coefficient 是一種兩個樣本的相似性的度量函數(shù),上式中,假設正樣本 p 越大,dice 值越大,說明模型預測的越準,則應該 loss 值越小,因此 dice loss 的就變成了下式這也就是最終 dice loss 的樣子。
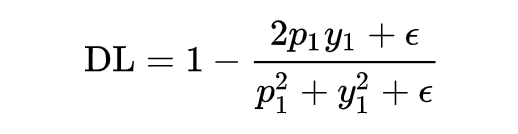
為了能得到 focal loss 同樣的功能,讓 dice loss 集中關注預測不準的樣本,可以與 focal loss 一樣加上一個調節(jié)系數(shù) ,就得到了香儂提出的適用于 NLP 任務的自調節(jié) DSC-Loss。
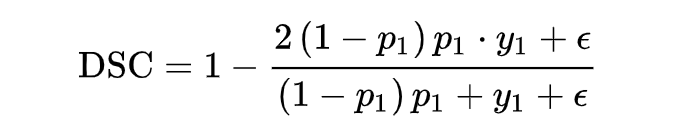
弄明白了原理,看下代碼的實現(xiàn)。
class DSCLoss(torch.nn.Module):
def __init__(self, alpha: float = 1.0, smooth: float = 1.0, reduction: str = “mean”): super().__init__() self.alpha = alpha self.smooth = smooth self.reduction = reduction
def forward(self, logits, targets): probs = torch.softmax(logits, dim=1) probs = torch.gather(probs, dim=1, index=targets.unsqueeze(1))
probs_with_factor = ((1 - probs) ** self.alpha) * probs loss = 1 - (2 * probs_with_factor + self.smooth) / (probs_with_factor + 1 + self.smooth)
if self.reduction == “mean”: return loss.mean()
總結
本文主要討論了類別不均衡問題的解決辦法,可分為數(shù)據(jù)層面的重采樣及模型 loss 方面的改進,如 focal loss, dice loss 等。最后說一下實踐下來的經(jīng)驗,由于不同數(shù)據(jù)集的數(shù)據(jù)分布特點各有不同,dice loss 以及 GHM loss 會出現(xiàn)些抖動、不穩(wěn)定的情況。當不想挨個實踐的時候,首推 focal loss,dice loss。
以上所有 Loss 的代碼僅為邏輯參考,完整的代碼及相關參考論文都在:
https://github.com/shuxinyin/NLP-Loss-Pytorch
審核編輯:郭婷
-
數(shù)據(jù)
+關注
關注
8文章
6713瀏覽量
88300 -
代碼
+關注
關注
30文章
4670瀏覽量
67760
原文標題:類別不均衡問題之loss大集合:focal loss, GHM loss, dice loss 等等
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
相關推薦
信道均衡的原理和分類介紹
調速器的主要分類和運轉方式
終結難題的發(fā)明(一):蓄電池均衡系統(tǒng)及其控制方法
電機的分類有哪些
PLC總線的分類方式
視頻網(wǎng)站服務器的四種負載均衡技術
深入理解 AFE 的用法:實現(xiàn)BMS?均衡功能
機器學習多分類任務深度解析
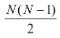




 數(shù)據(jù)類別不均衡問題的分類及解決方式
數(shù)據(jù)類別不均衡問題的分類及解決方式










評論