［導(dǎo)讀］ 在工程應(yīng)用時，有時候需要計算兩個信號序列的相似度，實際信號由于在采集過程中會混入干擾，如果簡單的依次比較各樣本是否相等或者差值，則很難判定兩個信號序列的相似程度。本文來聊聊我的一些思路。

什么是互相關(guān)函數(shù)？在統(tǒng)計學(xué)中，相關(guān)是描述兩個隨機變量序列或二元數(shù)據(jù)之間的統(tǒng)計關(guān)系，無論是否具有因果關(guān)系。廣義上講，相關(guān)性是統(tǒng)計上的關(guān)聯(lián)程度，它通常指的是兩個變量的線性相關(guān)的程度。比如商品的價格和消費者購買愿意數(shù)量之間的關(guān)系，也即所謂的需求曲線。

相關(guān)性是有用的，因為它們可以描述一種可在實踐中加以利用的預(yù)測作用。例如，根據(jù)電力需求和天氣之間的相關(guān)性，電力公司可能會在天氣涼快時候生產(chǎn)更少的電力。在這個例子中，有一定的因果關(guān)系存在，因為極端天氣導(dǎo)致人們使用更多的電力用于取暖或制冷。然而，一般而言，相關(guān)性的存在并不足以推斷出因果關(guān)系的存在，也就是說相關(guān)性并不意味著因果關(guān)系。

連續(xù)信號里，為函數(shù)及的互相關(guān)函數(shù)定義為：

離散信號，假設(shè)兩個信號序列x（n）及y（n），每個序列的能量都是有限能量序列，則x（n）及y（n）的互相關(guān)序列為：

那么互相關(guān)函數(shù)就是描述在連續(xù)信號或離散序列的相關(guān)程度的一種統(tǒng)計度量。

什么是相關(guān)系數(shù)？最熟悉的度量兩個量之間的相關(guān)性的方法是皮爾遜乘積矩相關(guān)系數(shù)（PPMCC），也稱為“皮爾遜相關(guān)系數(shù)”，通常簡稱為“相關(guān)系數(shù)”。在數(shù)學(xué)上，它被定義為對原始數(shù)據(jù)的最小二乘擬合的質(zhì)量（擬合程度或效果）。它是由數(shù)據(jù)集兩個變量的協(xié)方差的比率，歸一化到他們的方差的平方根得到的。數(shù)學(xué)上，兩個變量的協(xié)方差除以標準差的乘積。

皮爾遜積矩相關(guān)系數(shù)試圖通過兩個隨機序列的數(shù)據(jù)集建立一條最佳擬合曲線，實質(zhì)上是通過列出期望和由此產(chǎn)生的皮爾遜相關(guān)系數(shù)表明實際數(shù)據(jù)集離預(yù)期值有多遠。根據(jù)皮爾遜相關(guān)系數(shù)的符號，如果數(shù)據(jù)集的變量之間存在某種關(guān)系，可以得到負相關(guān)或正相關(guān)。其定義公式如下：

上述公式展開為：

在根據(jù)期望計算公式展開，就得到：

如果考察延遲d處的互相關(guān)，則上述公式就變?yōu)椋?/p>

為了方便理解，本文就不考察延遲節(jié)拍了。

相關(guān)系數(shù)有啥用？皮爾遜相關(guān)系數(shù)的絕對值不大于1是Cauchy–Schwarz不等式的推論（有興趣的可以去找書看看）。因此，相關(guān)系數(shù)的值在［-1，1］之間。在理想的增加線性相關(guān)關(guān)系情況下，相關(guān)系數(shù)為+1；在理想的減少（反相關(guān)）線性關(guān)系情況下，相關(guān)系數(shù)為-1；在所有其他取值情況下，表示變量之間的線性相關(guān)程度。當(dāng)它接近零時，更接近于不相關(guān)。系數(shù)越接近-1或1，變量之間的相關(guān)性越強。

故，相關(guān)系數(shù)其值范圍分布在區(qū)間［-1，1］：

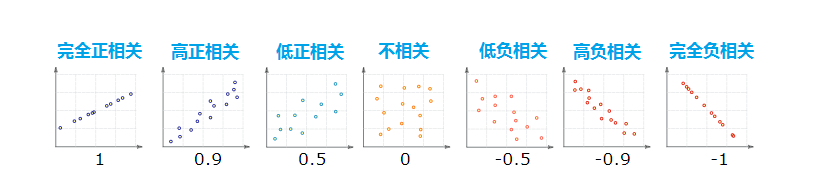
1表示完全正相關(guān)

0表示不相關(guān)

-1表示完全負相關(guān)

為了方便理解，假定兩個隨機序列按照下面各類情況分布，下面的數(shù)字為相關(guān)系數(shù)：

程序如何實現(xiàn)呢？上述公式在實際編程時，當(dāng)然可以直接按照公式編制代碼，如果仔細觀察會發(fā)現(xiàn)該公式可以進一步簡化，過程省略：

由這個公式就很容易編程了，干貨在這里，可以拿去稍加改造即可使用：

#include 《stdio.h》#include 《math.h》/* 返回值在區(qū)間： ［-1，1］ *//* 如返回-10，則證明輸入參數(shù)無效 */#define delta 0.0001fdouble calculate_corss_correlation（double *s1， double *s2，int n）

{

double sum_s12 = 0.0;

double sum_s1 = 0.0;

double sum_s2 = 0.0;

double sum_s1s1 = 0.0; //s1^2

double sum_s2s2 = 0.0; //s2^2

double pxy = 0.0;

double temp1 = 0.0;

double temp2 = 0.0;

if（ s1==NULL || s2==NULL || n《=0）

return -10;

for（int i=0;i《n;i++）

{

sum_s12 += s1［i］*s2［i］;

sum_s1 += s1［i］;

sum_s2 += s2［i］;

sum_s1s1 += s1［i］*s1［i］;

sum_s2s2 += s2［i］*s2［i］;

}

temp1 = n*sum_s1s1-sum_s1*sum_s1;

temp2 = n*sum_s2s2-sum_s2*sum_s2;

/* 分母不可為0 */

if（ （temp1》-delta && temp1《delta） ||

（temp2》-delta && temp2《delta） ||

（temp1*temp2《=0） ）

{

return -10;

}

pxy = （n*sum_s12-sum_s1*sum_s2）/sqrt（temp1*temp2）;

return pxy;

}

double s1［30］ = {

0.309016989，0.587785244，0.809016985，0.95105651，1，0.951056526，

0.809017016，0.587785287，0.30901704，5.35898E-08，0，0，

0，0，0，0，0，0，

0，0，0，0，0，0，

0，0，0，0，0，0

};

double s2［30］ = {

0.343282816，0.686491368，0.874624132，0.99459642，1.008448609，

1.014252458，0.884609221，0.677632906，0.378334666，0.077878732，

0.050711886，0.066417083，0.088759401，0.005440732，0.04225661，

0.035349939，0.0631196，0.007566056，0.053183895，0.073143706，

0.080285063，0.030110227，0.044781145，0.01875573，0.08373928，

0.04550342，0.038880858，0.040611891，0.046116826，0.087670453

};

int main（void）

{

double pxy;

double s3［30］;

pxy = calculate_corss_correlation（s1，s2，30）;

printf（“pxy of s1 and s2：%f

”，pxy）;

pxy = calculate_corss_correlation（s1，s1，30）;

printf（“pxy of s1 and s1：%f

”，pxy）;

for（int i=0;i《n;i++）

{

s3［i］ = -1*s1［i］;

}

pxy = calculate_corss_correlation（s1，s3，30）;

printf（“pxy of s1 and s3：%f

”，pxy）;

return 0;

}

運行結(jié)果為：

pxy of s1 and s2:0.997435

pxy of s1 and s1:1.000000

pxy of s1 and s1：-1.000000

將這三個信號繪制成波形來看看：

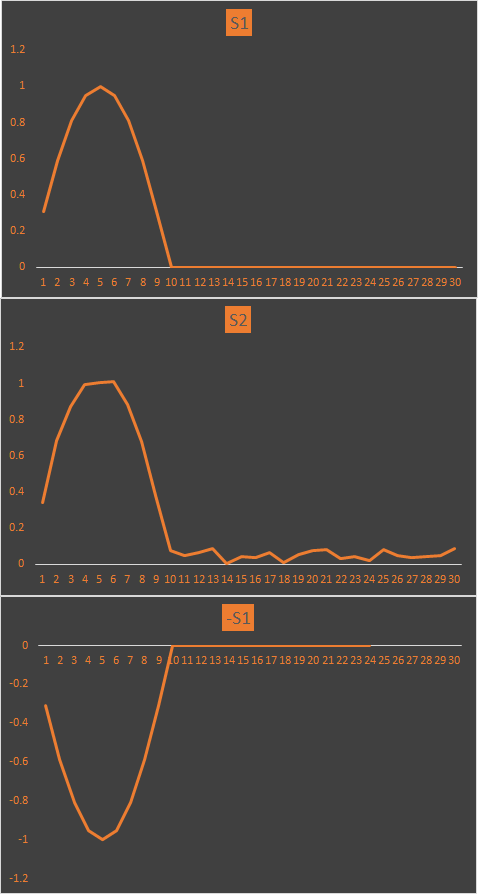
由圖看出：

S1與S2非常相似，其相關(guān)系數(shù)為0.997435，高度相似

S1與-S1則剛好相位相反，理想反相關(guān)，其相關(guān)系數(shù)為-1

S1與S1則理所當(dāng)然是一樣的，其相關(guān)系數(shù)為1

再來一組信號對比一下：

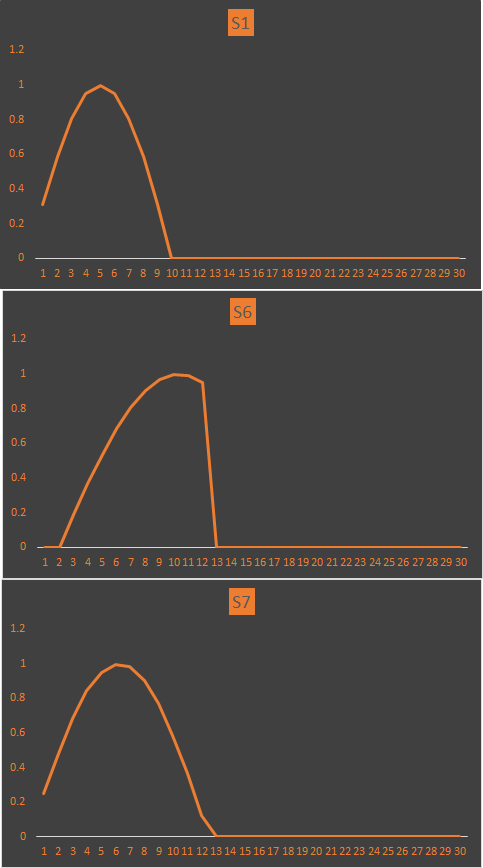
其波形數(shù)據(jù)為：

double s1［30］={

0.309016989，0.587785244，0.809016985，0.95105651，1，

0.951056526，0.809017016，0.587785287，0.30901704，5.35898E-08，

0，0，0，0，0，

0，0，0，0，0，

0，0，0，0，0，

0，0，0，0，0

};

double s6［30］={

0，0，0.187381311，0.368124547，0.535826787，

0.684547097，0.809016985，0.904827044，0.968583156，0.998026727，

0.992114705，0.951056526，0，0，0，

0，0，0，0，0，

0，0，0，0，0，

0，0，0，0，0

};

double s7［30］={

0.187381311，0.368124547，0.535826787，0.684547097，0.809016985，

0.904827044，0.968583156，0.998026727，0.992114705，0.951056526，

0.876306697，0.770513267，0.637424022，0.481753714，0，

0，0，0，0，0，

0，0，0，0，0，

0，0，0，0，0

};

利用上述代碼計算S1與S6，S1與S7的相關(guān)系數(shù)：

pxy of s1 and s6:0.402428

pxy of s1 and s7:0.612618

可見，S6、S7與S1的相關(guān)系數(shù)越來越大，從波形上看相似度也越來越大。

總結(jié)一下通過相關(guān)系數(shù)可以比較完美的判斷兩個信號序列，或者兩個隨機變量之間的相似度。相關(guān)系數(shù)以及互相關(guān)函數(shù)應(yīng)用很廣，本文僅僅描述了一個工程上應(yīng)用較多的實際栗子。事實上，該數(shù)學(xué)特性有著廣泛的應(yīng)用，有興趣的可以深度學(xué)習(xí)探討一下。

原文標題：數(shù)學(xué)之美：判定兩個隨機信號序列的相似度

文章出處：【微信公眾號：FPGA之家】歡迎添加關(guān)注！文章轉(zhuǎn)載請注明出處。