Python實(shí)現(xiàn)所有算法-力系統(tǒng)是否靜態(tài)平衡
Python實(shí)現(xiàn)所有算法-力系統(tǒng)是否靜態(tài)平衡(補(bǔ)篇)
Python實(shí)現(xiàn)所有算法-高斯消除法
Python實(shí)現(xiàn)所有算法-牛頓-拉夫遜(拉弗森)方法
Python實(shí)現(xiàn)所有算法-雅可比方法(Jacobian)
Python實(shí)現(xiàn)所有算法-矩陣的LU分解
Python實(shí)現(xiàn)所有算法-牛頓前向插值
兄弟們!今天的簡(jiǎn)單,我直接給大家表演徒手求導(dǎo)。
求導(dǎo)是數(shù)學(xué)計(jì)算中的一個(gè)計(jì)算方法,它的定義就是,當(dāng)自變量的增量趨于零時(shí),因變量的增量與自變量的增量之商的極限。在一個(gè)函數(shù)存在導(dǎo)數(shù)時(shí),稱這個(gè)函數(shù)可導(dǎo)或者可微分。可導(dǎo)的函數(shù)一定連續(xù)。不連續(xù)的函數(shù)一定不可導(dǎo)。
這個(gè)圖一定不可以錯(cuò)過(guò)

基本的做法是這樣的

對(duì)于一種數(shù)學(xué)的運(yùn)算,我們總是給出滿足的規(guī)則
其實(shí)哇,這些東西我寫(xiě)的沒(méi)有意義,在座的各位都學(xué)過(guò)高等數(shù)學(xué),數(shù)學(xué)分析,而且高中還學(xué)了兩年。概念不是啥問(wèn)題。
如果是為了科普,我推薦這本可愛(ài)的漫畫(huà)書(shū)(是數(shù)學(xué)書(shū)啦~)
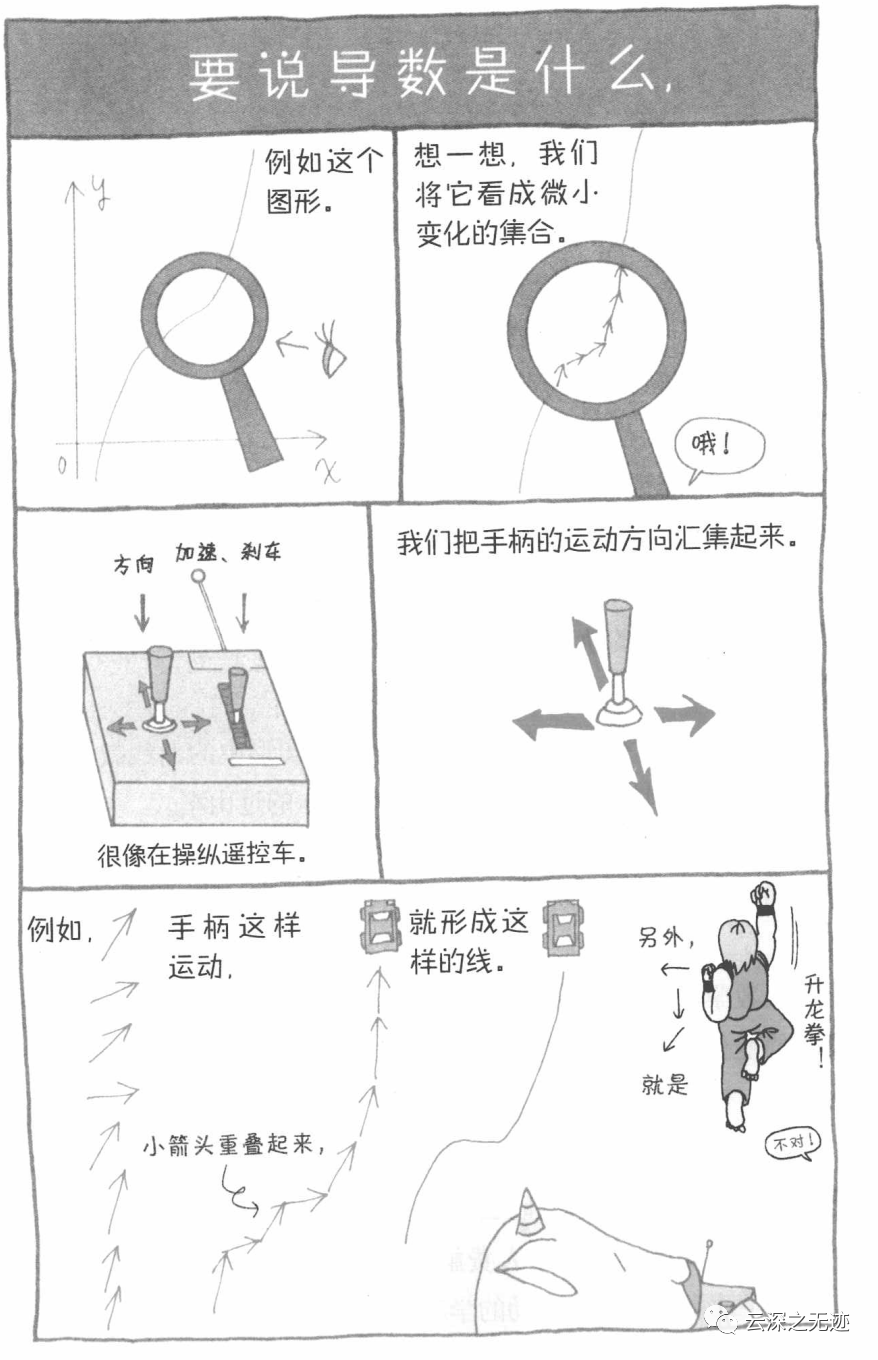
給大家看一個(gè)簡(jiǎn)單的頁(yè)面,是不是很有趣
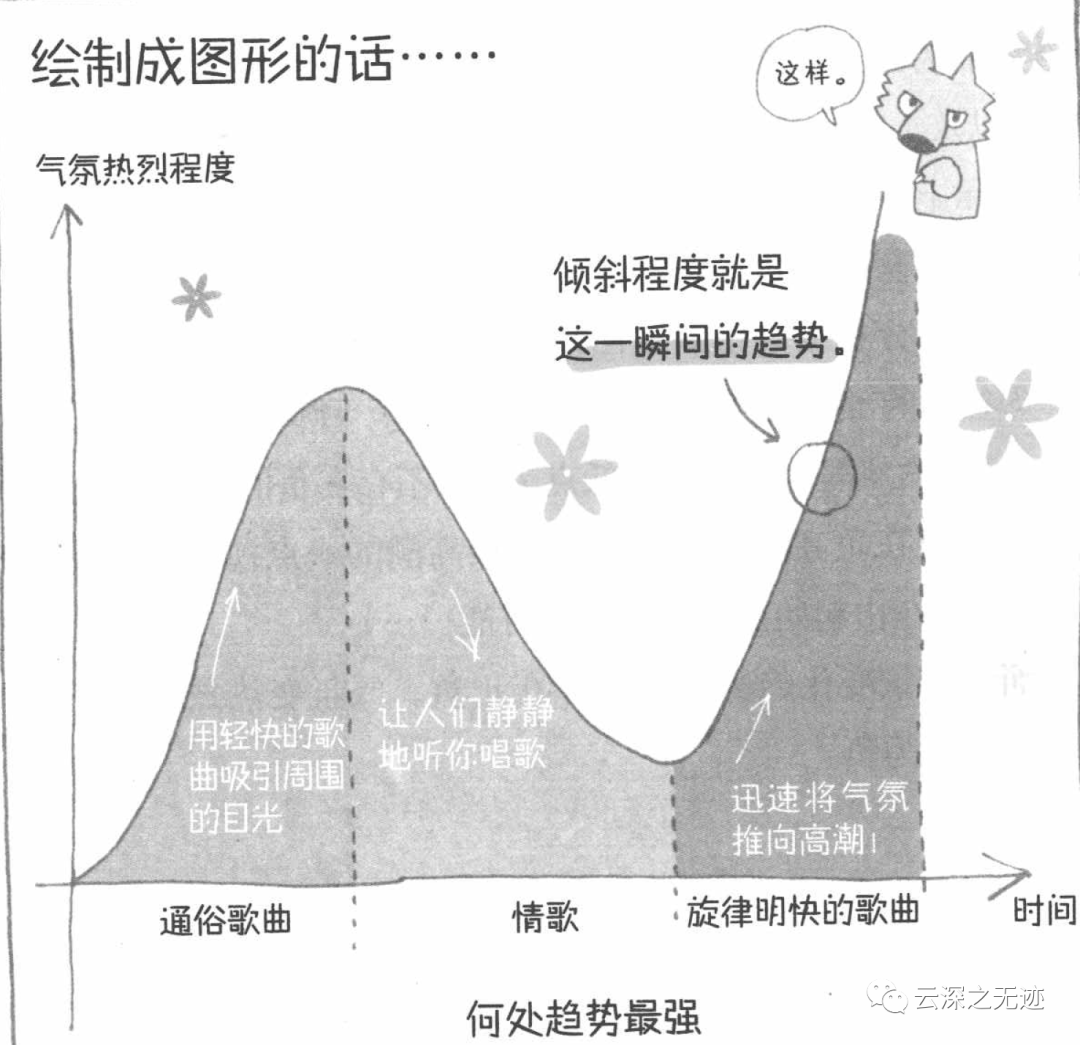
對(duì)一首歌的趨勢(shì)的曲線說(shuō)明
書(shū)中的內(nèi)容可能不深,但是這種寓教于樂(lè)的方式真的很好,至少這就是大眾接受的數(shù)學(xué)。
其次我推薦這本書(shū),你有沒(méi)有想過(guò)微積分風(fēng)風(fēng)雨雨這么多年,誕生之初是什么樣的?

本書(shū)給你答案
這本書(shū)我可太喜歡了,點(diǎn)到為止,是我對(duì)本書(shū)的評(píng)價(jià),是一本真的可以一本書(shū)讀下去的數(shù)學(xué)書(shū)。

隨便截圖一個(gè),點(diǎn)明對(duì)我們的需求來(lái)說(shuō),這樣就足夠了

非常的簡(jiǎn)潔,很OK

還有一套是托馬斯微積分,awesome的好書(shū),1k5多的頁(yè)數(shù),讓人直呼過(guò)癮

另外張景中院士的直來(lái)直去微積分真的很有特色,本書(shū)的特點(diǎn)是不使用極限和無(wú)窮小的概念,直截了當(dāng)?shù)慕o出函數(shù)的基本概念。

這段話是對(duì)書(shū)的最好詮釋

真的這些書(shū)給人以舍不得讀下去的感覺(jué),因?yàn)樽x完就沒(méi)有了

如果上面的你覺(jué)得太簡(jiǎn)單了,微積分筆記這本書(shū)是對(duì)于數(shù)學(xué)分析方方面面的一個(gè)題集總結(jié)。

有代表性的習(xí)題加上簡(jiǎn)短的定理總結(jié),不可多得好書(shū)

因?yàn)長(zhǎng)atex的排版,在美觀上面也是香的一比

emmmm,如果你想在通俗和嚴(yán)謹(jǐn)之間得到一個(gè)平衡,我個(gè)人覺(jué)得經(jīng)濟(jì)學(xué)的教材是很好的。

最后讓我再推薦一下黃皮書(shū),yyds!!!

同系列的還有這本,還有一本是線性代數(shù)就該這樣學(xué)
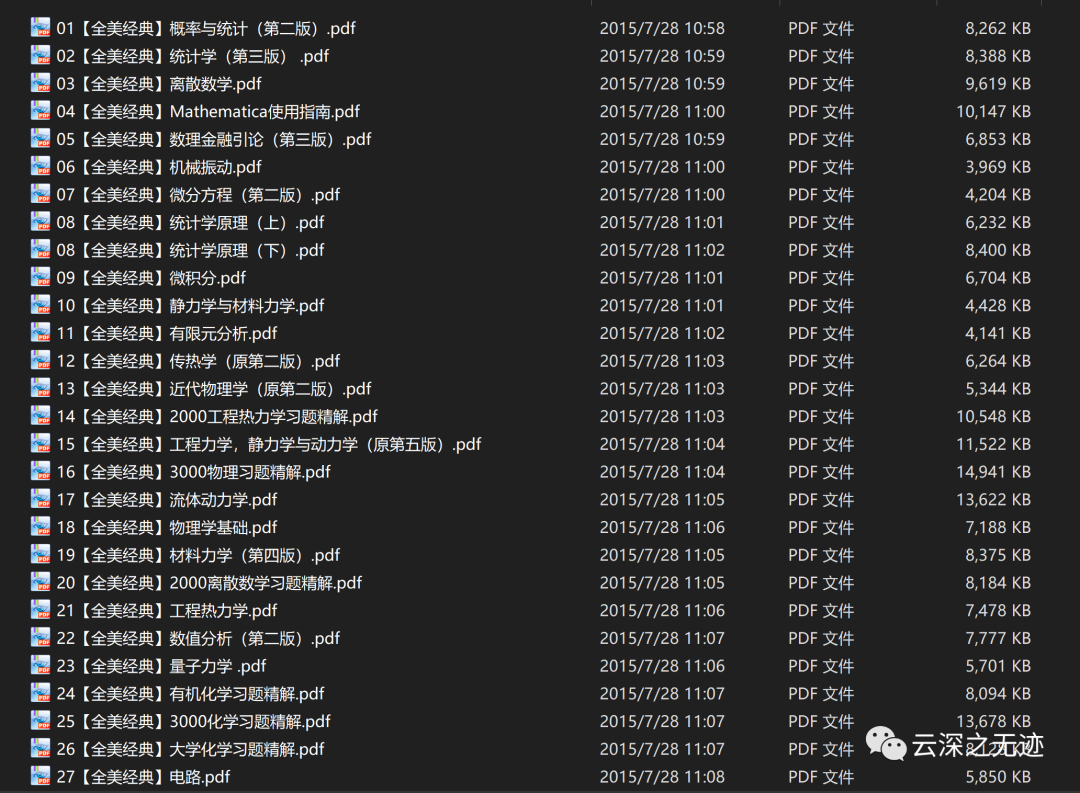
在最后讓我隆重的安利一下,全美經(jīng)典的教材,統(tǒng)計(jì)學(xué)原理講的真的是NO.1

內(nèi)容豐富嗷
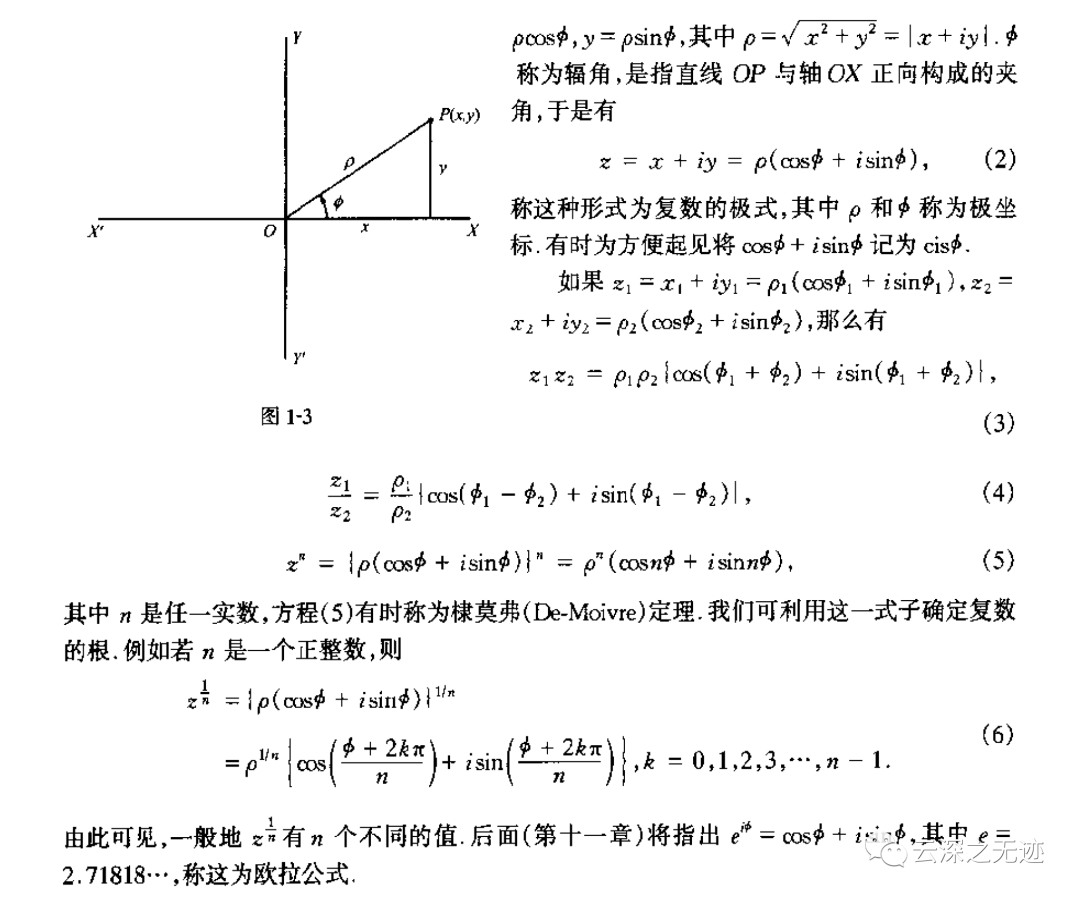
內(nèi)容也很好,推薦一讀
按照我老師的說(shuō)法,我的理論已經(jīng)ok了,所以要拉我去做題,emmmm。
這個(gè)我不用多說(shuō)吧???
事實(shí)上,這次要講的確實(shí)是求導(dǎo),但是比哪個(gè)東西高級(jí)。
在微積分中,牛頓法是一種迭代方法,用于求可微函數(shù)F的根,它是方程F ( x ) = 0的解。因此,牛頓法可以應(yīng)用于二次可微函數(shù)f的導(dǎo)數(shù)f ‘以求導(dǎo)數(shù)的根(f ’( x ) = 0的解),也稱為f的臨界點(diǎn) 。 這些解可能是最小值、最大值或鞍點(diǎn)。這與優(yōu)化有關(guān),優(yōu)化旨在找到函數(shù)f的(全局)最小值。
優(yōu)化的核心問(wèn)題是函數(shù)的最小化。讓我們首先考慮單變量函數(shù)的情況,即單個(gè)實(shí)變量的函數(shù)。
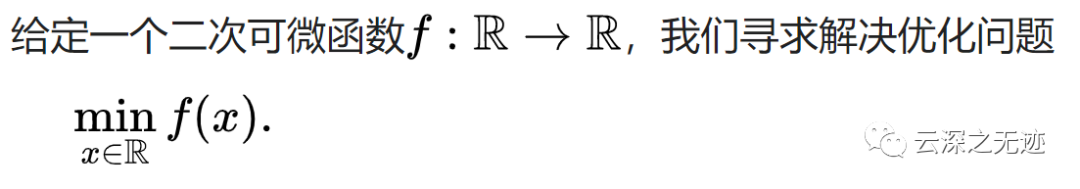
找最小
這是基本牛頓法:

理論是這樣的
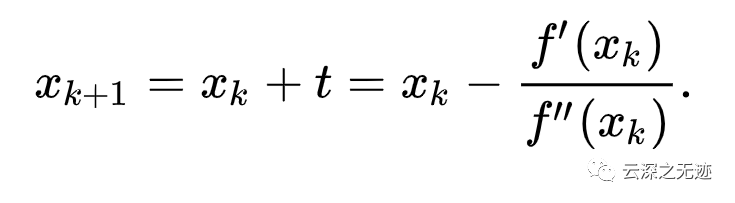
這是最終的更新公式
接下來(lái)再細(xì)講,并不是所有的方程都有求根公式,或者求根公式很復(fù)雜,導(dǎo)致求解困難。利用牛頓法,可以迭代求解。
原理是利用泰勒公式,在x0處展開(kāi),且展開(kāi)到一階,即f(x) = f(x0)+(x-x0)f‘(x0)
求解方程f(x)=0,即f(x0)+(x-x0)*f’(x0)=0,求解x = x1=x0-f(x0)/f‘(x0),因?yàn)檫@是利用泰勒公式的一階展開(kāi),f(x) = f(x0)+(x-x0)f’(x0)處并不是完全相等,而是近似相等,這里求得的x1并不能讓f(x)=0,只能說(shuō)f(x1)的值比f(wàn)(x0)更接近f(x)=0,于是乎,迭代求解的想法就很自然了,可以進(jìn)而推出x(n+1)=x(n)-f(x(n))/f‘(x(n)),通過(guò)迭代,這個(gè)式子必然在f(x*)=0的時(shí)候收斂。整個(gè)過(guò)程如下圖:
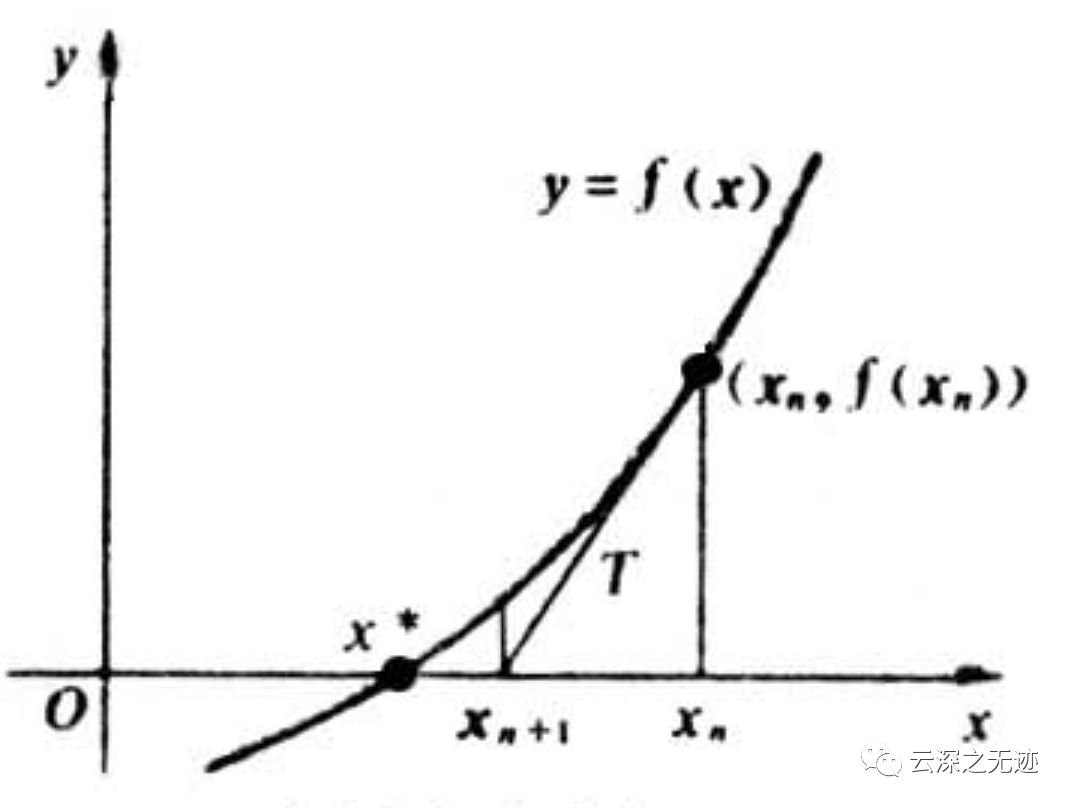
這是求根
接下來(lái)是最優(yōu)化,對(duì)一個(gè)目標(biāo)函數(shù)f,求函數(shù)f的極大極小問(wèn)題,可以轉(zhuǎn)化為求解函數(shù)f的導(dǎo)數(shù)f’=0的問(wèn)題,這樣求可以把優(yōu)化問(wèn)題看成方程求解問(wèn)題(f‘=0)。
剩下的問(wèn)題就和第一部分提到的牛頓法求解很相似了。為了求解f’=0的根,把f(x)的泰勒展開(kāi),展開(kāi)到2階形式:
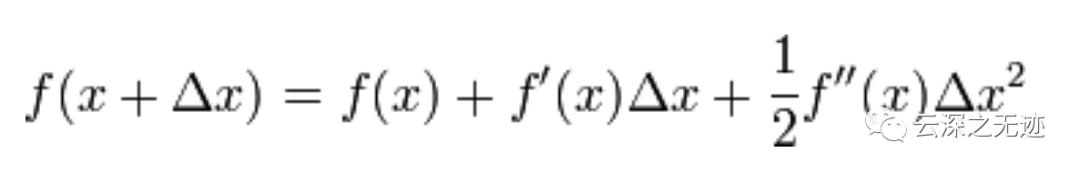
當(dāng)且小三角無(wú)限趨于0 的時(shí)候
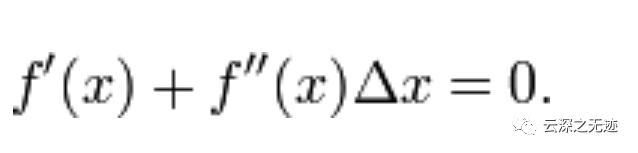
這個(gè)成立
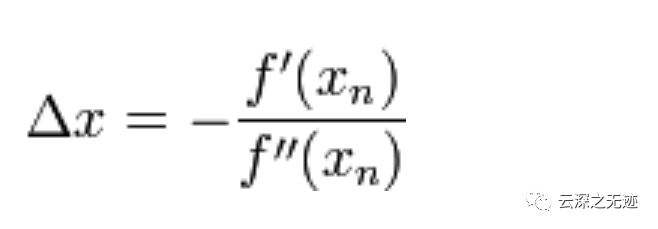
我們的最終迭代公式就出來(lái)了
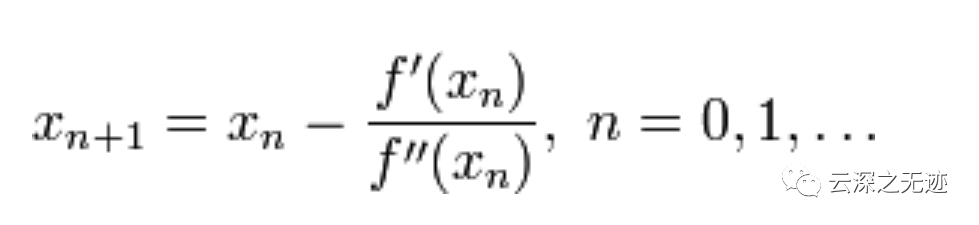
值得更新公式
牛頓法用于函數(shù)最優(yōu)化求解”中對(duì)函數(shù)二階泰勒公式展開(kāi)求最優(yōu)值的方法稱為:Newton法,
牛頓法用于方程求解”中對(duì)函數(shù)一階泰勒展開(kāi)求零點(diǎn)的方法稱為:Guass-Newton(高斯牛頓)法。
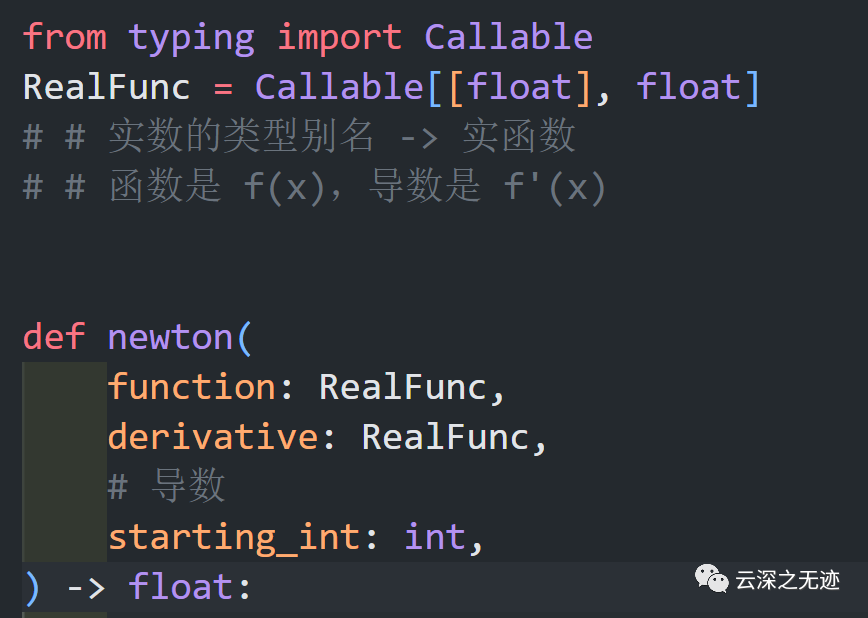
這次得比較難。。。就提前寫(xiě)好求導(dǎo):
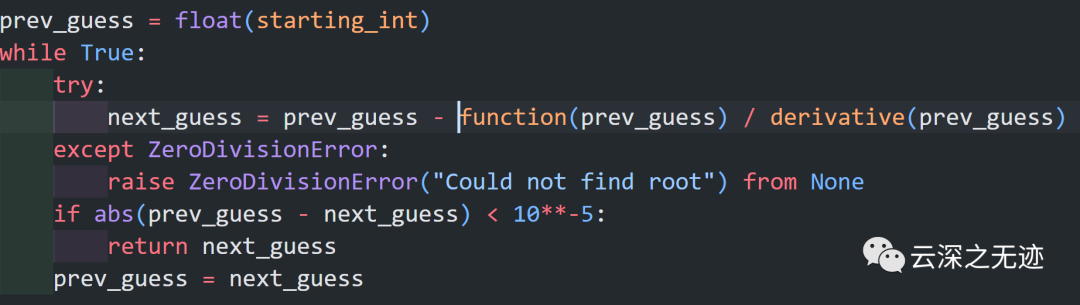
這個(gè)公式就是上面的更新公式

我們提前把函數(shù)和求導(dǎo)的函數(shù)寫(xiě)好

原文標(biāo)題:Python實(shí)現(xiàn)所有算法-牛頓優(yōu)化法
文章出處:【微信公眾號(hào):云深之無(wú)跡】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4308瀏覽量
62445 -
牛頓
+關(guān)注
關(guān)注
0文章
6瀏覽量
6328 -
python
+關(guān)注
關(guān)注
56文章
4783瀏覽量
84473
原文標(biāo)題:Python實(shí)現(xiàn)所有算法-牛頓優(yōu)化法
文章出處:【微信號(hào):TT1827652464,微信公眾號(hào):云深之無(wú)跡】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
三種常見(jiàn)平方根算法的電路設(shè)計(jì)及Verilog實(shí)現(xiàn)與仿真
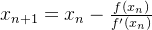
【「從算法到電路—數(shù)字芯片算法的電路實(shí)現(xiàn)」閱讀體驗(yàn)】+內(nèi)容簡(jiǎn)介
【「從算法到電路—數(shù)字芯片算法的電路實(shí)現(xiàn)」閱讀體驗(yàn)】+一本介紹基礎(chǔ)硬件算法模塊實(shí)現(xiàn)的好書(shū)
如何使用Python實(shí)現(xiàn)PID控制
Python建模算法與應(yīng)用
如何實(shí)現(xiàn)Python復(fù)制文件操作
神經(jīng)網(wǎng)絡(luò)的基本原理及Python編程實(shí)現(xiàn)
如何用C語(yǔ)言實(shí)現(xiàn)高效查找(二分法)

網(wǎng)孔電流法和回路電流法怎么選擇比較好
同步置數(shù)法和異步清零法的優(yōu)缺點(diǎn) 異步計(jì)數(shù)器的級(jí)聯(lián)方法總結(jié)
通過(guò)Python腳本實(shí)現(xiàn)WIFI密碼的自動(dòng)猜解




 Python實(shí)現(xiàn)所有算法-基本牛頓法
Python實(shí)現(xiàn)所有算法-基本牛頓法










評(píng)論