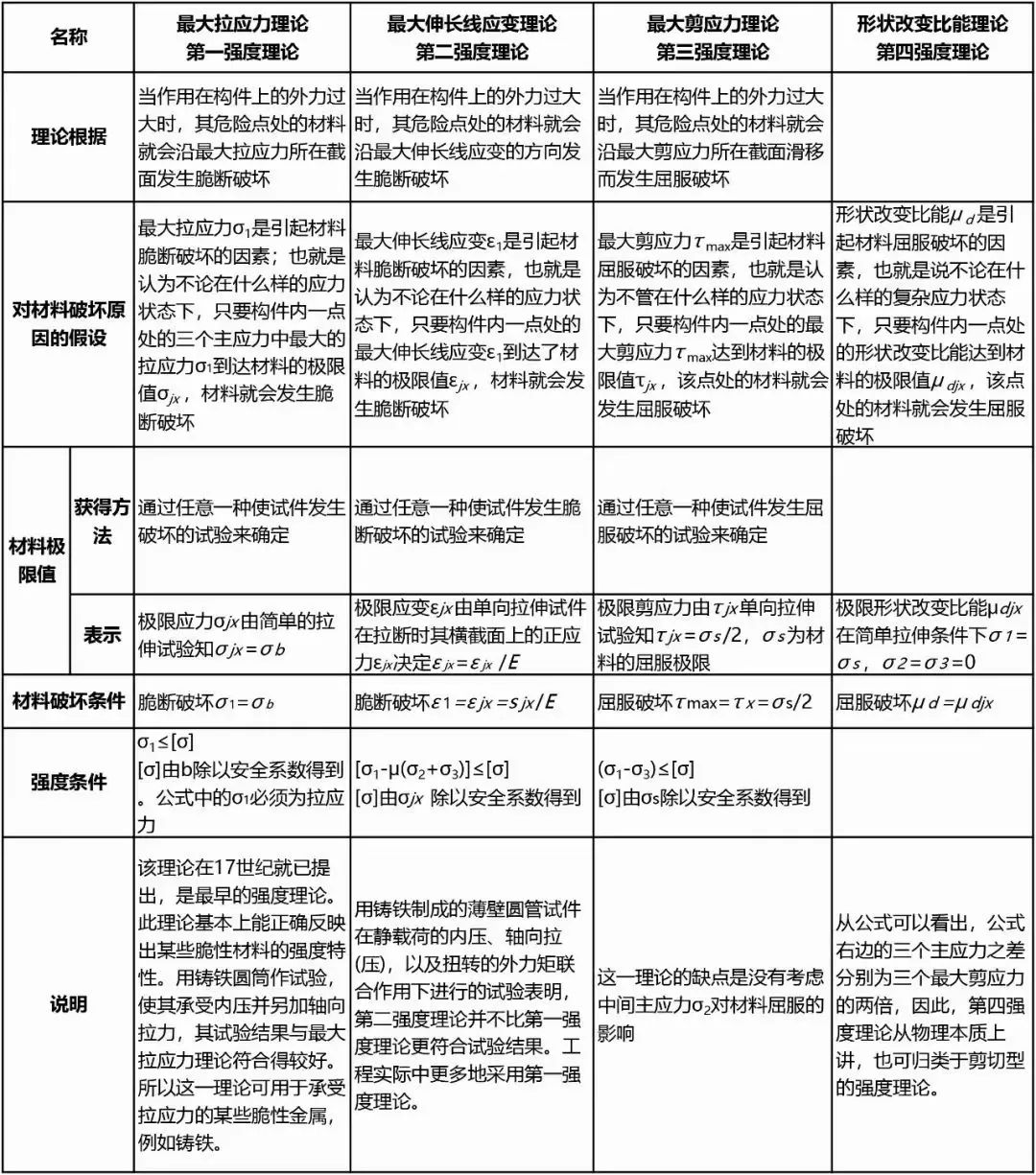
由于材料的破壞按其物理本質分為脆斷和屈服兩類形式,所以,強度理論也就相應地分為兩類,下面就來介紹目前常用的四個強度理論。
1、最大拉應力理論(第一強度理論即最大主應力):
這一理論又稱為第一強度理論。這一理論認為破壞主因是最大拉應力。不論復雜、簡單的應力狀態,只要第一主應力達到單向拉伸時的強度極限,即斷裂。
破壞形式:斷裂。
破壞條件:σ1 =σb
強度條件:σ1≤[σ]
實驗證明,該強度理論較好地解釋了石料、鑄鐵等脆性材料沿最大拉應力所在截面發生斷裂的現象;而對于單向受壓或三向受壓等沒有拉應力的情況則不適合。
缺點:未考慮其他兩主應力。
使用范圍:適用脆性材料受拉。如鑄鐵拉伸,扭轉。
2、最大伸長線應變理論(第二強度理論即最大主應變)
這一理論又稱為第二強度理論。這一理論認為破壞主因是最大伸長線應變。不論復雜、簡單的應力狀態,只要第一主應變達到單向拉伸時的極限值,即斷裂。破壞假設:最大伸長應變達到簡單拉伸的極限(假定直到發生斷裂仍可用胡克定律計算)。
破壞形式:斷裂。
脆斷破壞條件:ε1= εu=σb/E
ε1=1/E[σ1?μ(σ2+σ3)]
破壞條件:σ1?μ(σ2+σ3) = σb
強度條件:σ1?μ(σ2+σ3)≤[σ]
實驗證明,該強度理論較好地解釋了石料、混凝土等脆性材料受軸向拉伸時,沿橫截面發生斷裂的現象。但是,其實驗結果只與很少的材料吻合,因此已經很少使用。
缺點:不能廣泛解釋脆斷破壞一般規律。
使用范圍:適于石料、混凝土軸向受壓的情況。
3、 最大切應力理論(第三強度理論即Tresca強度):
這一理論又稱為第三強度理論。這一理論認為破壞主因是最大切應力
maxτ。不論復雜、簡單的應力狀態,只要最大切應力達到單向拉伸時的極限切應力值,即屈服。破壞假設:復雜應力狀態危險標志最大切應力達到該材料簡單拉、壓時切應力極限。
破壞形式:屈服。
破壞因素:最大切應力。
τmax=τu=σs/2
屈服破壞條件:τmax=1/2(σ1?σ3)
破壞條件:σ1?σ3= σs
強度條件:σ1?σ3≤[σ]
實驗證明,這一理論可以較好地解釋塑性材料出現塑性變形的現象。但是,由于沒有考慮2σ的影響,故按這一理論設計的構件偏于安全。
缺點:無2σ影響。
使用范圍:適于塑性材料的一般情況。形式簡單,概念明確,機械廣用。但理論結果較實際偏安全。
4、形狀改變比能理論(第四強度理論即von mises強度)
這一理論又稱為第四強度理論。這一理論認為:不論材料處在什么應力狀態,材料發材料力學生屈服的原因是由于形狀改變比能(du)達到了某個極限值。由此可建立如下
破壞條件:1/2(σ1?σ2)2+2(σ2?σ3)2+(σ3?σ1)2=σs
強度條件:σr4= 1/2(σ1?σ2)2+ (σ2?σ3)2+ (σ3?σ1)2≤[σ]
根據幾種材料(鋼、銅、鋁)的薄管試驗資料,表明形狀改變比能理論比第三強度理論更符合實驗結果。
四種強度理論的統一形式:令相當應力σrn,有強度條件統一表達式
σrn≤[σ]。
相當應力的表達式:
σr1=σ1≤[σ]
σr2=σ1?μ(σ2+σ3)≤[σ]
σr 3=σ1?σ3≤ [σ]
σr4= 1/2(σ1?σ2)2+(σ2?σ3)2+(σ3?σ1)2≤ [σ]
5、 莫爾強度理論
莫爾強度理論并不是簡單地假設材料的破壞是由某一個因素(例如應力、應變或比能)達到了其極限值而引起的,它是以各種應力狀態下材料的破壞試驗結果為依據,考慮了材料拉、壓強度的不同,承認最大切應力是引起屈服剪斷的主要原因并考慮了剪切面上正應力的影響而建立起來的強度理論。
莫爾強度理論考慮了材料抗拉和抗壓能力不等的情況,這符合脆性材料
(如巖石混凝土等)的破壞特點,但未考慮中間主應力2σ的影響是其不足之處。
6.強度理論的適用范圍
不僅取決于材料的性質,而且還與危險點處的應力狀態有關。一般情況下,脆性材料選用關于脆斷的強度理論與莫爾強度理論,塑性材料選用關于屈服的強度理論。但材料的失效形式還與應力狀態有關。例如,無論是塑性或脆性材料,在三向拉應力情況下將以斷裂形式失效,宜采用最大拉應力理論。在三向壓應力情況下都引起塑性變形,宜采用第三或第四強度理論。
審核編輯 :李倩
-
強度
+關注
關注
0文章
5瀏覽量
15915 -
拉伸
+關注
關注
0文章
6瀏覽量
6751
原文標題:四大強度理論概述
文章出處:【微信號:AMTBBS,微信公眾號:世界先進制造技術論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
IGBT的四個主要參數
有源晶振四個腳是如何定義的?





 常用的四個強度理論
常用的四個強度理論











評論