既有大小又有方向的量,稱為向量,同學們在學習這一部分數學知識時,似乎感到困惑:向量到底有什么用?今天,小編就和大家來聊一聊向量.
1 力與向量
向量的英文是,中國的物理學家們在清末民初時期引進西方科學概念時將“”稱為“矢量”,至今向量與矢量兩種譯名共存,究其原因,早期的向量只是物理學專門用來表示力和速度等“既有大小又有方向”的物理量的工具,并不為數學家們所重視,因此“矢量”的譯名一度流行.
實際上,力作為向量最常見的實例有著十分古老的淵源.大約在公元前350年,古希臘著名學者亞里士多德就知道了力可以表示成向量,兩個力的合力可用平行四邊形法則得到,隨后古希臘數學家海倫則給出了該法則的幾何證明.
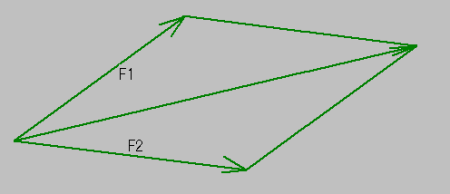
力的合成
在現實生活中,處處有“力的平行四邊形法則”,比如中國古代的“駟馬車”,可以直觀地依據平行四邊形法則觀察到這樣的合力.
古希臘之后的1500多年,經過了漫長又黑暗的中世紀,向量的知識都沒有什么太大的變化.牛頓在其著作《自然哲學的數學原理》中總結了前人的智慧,論述了力、速度等物理量作為矢量如何進行運算,其本質還是向量的平行四邊形法則.可見,這點向量知識,形不成多少有意義的數學問題,不能發展成一個獨立的學科,因此數學家們并沒有重點將向量作為對象進行深入地研究.
2 復數與向量
直到19世紀,事情開始發生變化,“復數”在向量的發展中充當了催化劑.
數學家韋塞爾和阿爾岡發現了復數的幾何表示,這是一個具有劃時代意義的數學發現,隨后德國數學家高斯建立了復平面的概念,從而使得平面向量與復數一一對應起來.向量可以表示為一組有序實數對,這與復平面中的復數是一致的.
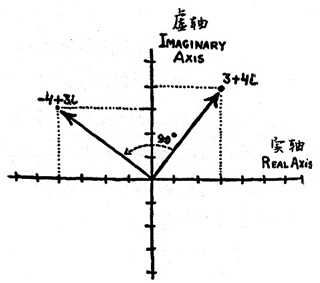
復數——數的最后樂章
當時的數學家們想到,復數可以看作“二維向量”,那么單個實數就可以看作“一維向量”,同理,一定也還有“三維向量”、“四維向量”,乃至“維向量”.
于是,愛爾蘭數學家哈密頓首先研究了“四元數”:
這種具有4個分量的數具有諸多神奇的性質,它構成的數系能夠進行加減乘除四則運算,但是美中不足的是要放棄乘法交換律.
盡管如此,這一偉大的發現引起了又一位大牛的注意,代表著19世紀物理學重要發展方向的著名物理學家麥克斯韋對四元數情有獨鐘,他對于四元數在電磁學中的應用使人們逐步認識到用向量處理物理問題的必要性.
麥克斯韋在其著作《電磁通論》的緒論中寫道:
“
對于物理推理的許多目的來說,不同于計算,有必要避免明確地引入笛卡爾坐標,并把注意力固定在一個空間點上而不是在它的3個坐標上,固定在一個力的大小和方向上而不是它的3個分量上.這種考慮幾何量和物理量的模式比另一種模式更原始、更自然,盡管與它相聯系的那些概念直到哈密頓通過發明他的四元數演算而在處理空間問題上邁出一大步才得到充分的發展.……然而,我確信,四元數的概念而不是四元數的運算和方法的引入,對我們的課題的所有部分的研究將是大有用處的;特別是在電動力學中,在那里我們必須討論許多物理量,而他們彼此之間的關系可以用哈密頓的少數幾個表達式來表示,比用普通的方程要簡單得多.
可見,隨著復數與向量理論的深入,物理學科的相關知識(尤其是電學)也得到了發展.
3 “四維向量”與中國古詩文化
提到四維向量,現在讓我們一起來欣賞初唐詩人陳子昂的著名詩篇《登幽州臺歌》,體會其中蘊含的數學文化意境:
“
前不見古人,后不見來者.念天地之悠悠,獨愴然而涕下!
這便是古人對時間與空間看法的文學表述.陳子昂的時空觀,就是歐幾里得的時空觀,也是今天人們普遍持有的樸素時空觀.
從數學上看,這是一首闡發時間與空間感知的絕妙佳作.前兩句表示時間可以看成一條直線(一維),以詩人自己為原點,前不見古人指時間可以延申至負無窮大,后不見來者則意味著未來的時間是正無窮大,后兩句則指向了“天和地”構成的三維現實空間.因此,如果此時此刻為,我們在三維空間中的位置為,那么每個人在“四維空間”中都對應了一個獨特的向量:
陳子昂在詩中感嘆天地之宏大,時間之遙遠,不禁覺人生之短暫,遂產生敬畏之心,這樣的意境,對于數學家和文學家來說是可以相通的.
4 維向量
沿著四維向量往前走,維向量逐漸被撥開迷霧展現在人們面前.
德國數學家格拉斯曼于1844年引入了維向量的概念.仿效平面向量的記法,我們將一個維向量定義為一個維的數組:
維向量可以定義加法和減法,也可以用單個實數與其相乘.向量的數量積也可以推廣到維情形.這就是向量空間(線性空間)要研究的問題.
實際上,維向量看似很“高端”,但是它在生活中其實有著非常直觀的意義,比如說我們去商場購物,種商品的“單價向量”
以及種商品的“數量向量”
那么兩者的數量積,實際上就是你的總付款金額
因此,所謂的維向量的數量積,其實就在我們身邊.
時至今日,“個”成為當今社會的流行語,用來表示“很多個”的意思,比如“我有個選擇”,“這件事有個因素”等等,究其根源,正是維向量等數學名詞廣泛普及的結果.
審核編輯:劉清
-
向量
+關注
關注
0文章
55瀏覽量
11658
原文標題:為什么要學習向量?
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 聊一聊向量到底有什么用
聊一聊向量到底有什么用











評論