現(xiàn)代 IRST（紅外瞄準(zhǔn)和跟蹤）傳感器可以有效跟蹤敵方目標(biāo)（在意大利，我們擁有出色的 Skyward-G，由 Selex Galileo 開發(fā)）。然而，達(dá)到目標(biāo)的問題仍然懸而未決。在本文中，我們提出了一種自動(dòng)跟蹤算法，其中目標(biāo)執(zhí)行回避隨機(jī)游走；另一方面，算法的收斂（即到達(dá)/摧毀目標(biāo)）是一個(gè)確定性的過程。

一點(diǎn)歷史

根據(jù)一個(gè)著名的軼事，在 1980 年代，斯德哥爾摩委員會(huì)沒有將諾貝爾獎(jiǎng)授予美國著名物理學(xué)家 R. Dicke，因?yàn)樗麑啄甑穆殬I(yè)生涯致力于實(shí)現(xiàn)紅外傳感器用于研究/跟蹤/殺死移動(dòng)目標(biāo)。更準(zhǔn)確地說，紅外搜索和跟蹤 （IRST） 傳感器檢測(cè)飛機(jī)廢氣發(fā)出的紅外輻射。1950 年代使用的第一個(gè)模型相當(dāng)原始，旋轉(zhuǎn)自由度降低。對(duì)此類探測(cè)器后續(xù)發(fā)展的一個(gè)顯著貢獻(xiàn)來自越南戰(zhàn)爭，這也歸功于迪克的開創(chuàng)性工作：新一代傳感器看到了美國響尾蛇導(dǎo)彈上的光。

維納濾波器和 IRST 傳感器

IRST 傳感器是飛機(jī)尾氣發(fā)出的紅外輻射的探測(cè)器。眾所周知，任何熱物體都會(huì)發(fā)射紅外范圍內(nèi)的電磁輻射。如果這種發(fā)射類似于在溫度T處處于熱力學(xué)平衡狀態(tài)的黑體，如果λ是發(fā)射輻射的波長，我們有位移定律：

其中λ max是發(fā)射功率最大的波長值。從這個(gè)方程可以看出，這個(gè)大小與溫度成反比。在IRST傳感器的實(shí)現(xiàn)中，需要參考一個(gè)溫度范圍（T 1 ，T 2），使波長落在紅外波段。為了更清楚，在圖 1 中，我們報(bào)告了作為無量綱變量hν / kT函數(shù)的發(fā)射功率趨勢(shì)，其中h是普朗克常數(shù)，k是玻爾茲曼常數(shù)，ν = c /λ 是發(fā)射頻率輻射 （ c是光速）。從溫度升高時(shí)繪制的曲線族中，我們看到隨著溫度升高，發(fā)射峰向高頻移動(dòng)。

從操作上講，IRST 傳感器是一種熱像儀，能夠檢測(cè) 2 之間波長范圍的紅外輻射。5 × 10 -8和 11 × 10 -8厘米。然而，主要問題是由于電磁場(chǎng)在紅外范圍內(nèi)在地球大氣層中傳播的能力很差。更準(zhǔn)確地說，紅外光子被大氣中存在的水蒸氣分子吸收。因此，為了獲得良好的效率，它們運(yùn)行的距離不得超過指定的閾值。此外，為了對(duì)目標(biāo)圖像進(jìn)行可能的軟件重建，需要為系統(tǒng)配備維納濾波器。1如果不是這樣，一群鳥很可能被誤認(rèn)為是敵機(jī)。

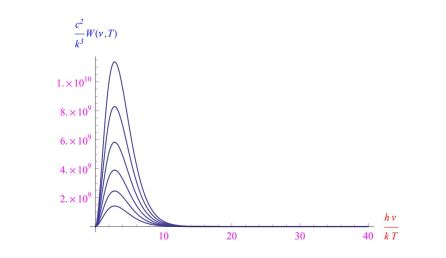
圖 1：黑體在溫度T的熱平衡中發(fā)射的功率密度趨勢(shì)（對(duì)于該量的不同值）作為無量綱變量hν / kT的函數(shù)

動(dòng)態(tài)設(shè)置

地面參考系

動(dòng)態(tài)設(shè)置跟蹤問題意味著編寫運(yùn)動(dòng)微分方程或應(yīng)用牛頓第二定律。因此，有必要指定一個(gè)慣性參考系。由于飛機(jī)速度比表征地球運(yùn)動(dòng)（繞軸自轉(zhuǎn)、繞太陽公轉(zhuǎn)）的相應(yīng)運(yùn)動(dòng)學(xué)量高幾個(gè)數(shù)量級(jí)，因此可以非常近似地認(rèn)為我們的星球是“靜止的”。因此，讓我們假設(shè)一個(gè)由笛卡爾坐標(biāo)軸組成的 Oxyz 三元組作為參考系統(tǒng) ，假設(shè)地球中心的原點(diǎn)為球形；x 軸在赤道平面內(nèi)并朝向腳 格林威治子午線（腳是子午線與赤道平面的交點(diǎn)）。在這種情況下，飛機(jī)的地理坐標(biāo)（緯度和經(jīng)度）和高度可以很容易地轉(zhuǎn)換為笛卡爾坐標(biāo)（x，y，z）。

時(shí)間分辨率和飛機(jī)機(jī)動(dòng)性

在這種動(dòng)態(tài)場(chǎng)景中， 配備 IRST 傳感器的攻擊者（導(dǎo)彈）A 必須檢測(cè)目標(biāo)（戰(zhàn)斗機(jī)）B。必須快速連續(xù)執(zhí)行檢測(cè)，以便能夠?qū)⑵渌俣仁噶恐赶蛩矔r(shí)位置的目標(biāo)。如果Δt 是表征上述序列的最小時(shí)間間隔，則檢測(cè)到的軌跡是真實(shí)軌跡中的一段。后者顯然是微分幾何意義上的平滑曲線。還必須考慮單個(gè)車輛的機(jī)動(dòng)性。為此，我們用 （ δt） A 和 （ δt） B表示 分別為 A 和 B 的機(jī)動(dòng)時(shí)間。由于戰(zhàn)斗機(jī)比導(dǎo)彈更機(jī)動(dòng)，我們預(yù)計(jì)以下雙重不等式：

換句話說，目標(biāo)的航向變化（即規(guī)避機(jī)動(dòng)）在攻擊者的時(shí)間尺度上是瞬時(shí)的，并且與Δt相比都小到可以忽略不計(jì)。這種情況表明忽略上述時(shí)間尺度。這相當(dāng)于假設(shè)兩架飛機(jī)都具有無限機(jī)動(dòng)性。最后，為了使問題在數(shù)學(xué)上更易于管理，我們執(zhí)行通過 Δ t → 0 的限制的操作。這相當(dāng)于直接考慮真實(shí)軌跡，將單個(gè)車輛通過一個(gè)質(zhì)點(diǎn)進(jìn)行模式化以忽略旋轉(zhuǎn)自由度。這種方法可能看起來不切實(shí)際，但它構(gòu)成了解決所提出問題的第一個(gè)近似步驟。

IRST 運(yùn)動(dòng)學(xué)

首先，我們觀察到追擊并不自動(dòng)意味著可達(dá)性：攻擊者 A 可以無限期地追擊目標(biāo) B，但從未到達(dá)目標(biāo) B。在任何情況下，重要的是通過以下方式數(shù)學(xué)表達(dá)以下條件逐步進(jìn)行。在圖 2 中，我們報(bào)告了飛機(jī)在通用時(shí)刻 t相對(duì)于地面參考系統(tǒng)的位置，其中 D （ t ） 是 距離向量，其模數(shù)是上述時(shí)刻 A 點(diǎn)和 B 點(diǎn)之間的歐幾里得距離。 但是讓我們通過指定圖中的符號(hào)來嘗試更清楚。

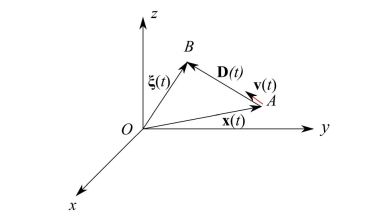
圖 2：飛機(jī)相對(duì)于指定的地面三元組的瞬時(shí)位置

這里，ξ （ t ） 是目標(biāo)的位置向量，即從原點(diǎn)向目標(biāo)瞬時(shí)位置標(biāo)記的向量：

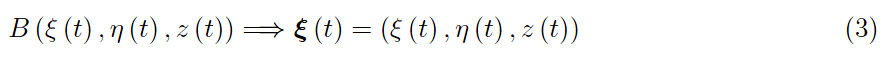
我們用希臘字母來區(qū)分它們與拉丁同音字，我們將用它來表示 A 的坐標(biāo)。實(shí)際上，后者位于

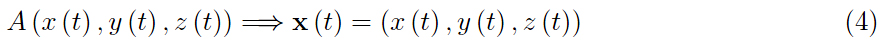
我們不知道目標(biāo)的坐標(biāo)，但是追擊的條件是通過強(qiáng)加 A 的速度矢量始終指向 B 的瞬時(shí)位置來表達(dá)的（換句話說，攻擊者沒有預(yù)料到目標(biāo)的移動(dòng)） 。 從向量演算中，我們知道兩個(gè)向量是平行且等價(jià)的當(dāng)且僅當(dāng)它們是成比例的并且比例的標(biāo)量是非負(fù)的：

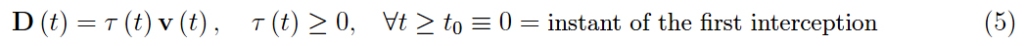
這個(gè)等式定義了“距離”向量：

其模塊是：

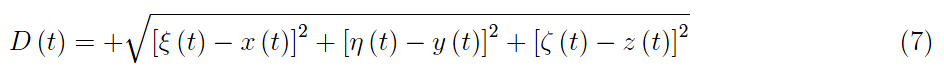
根據(jù)等式 5，我們有：

τ （t）的運(yùn)動(dòng)學(xué)意義 由此而來：這個(gè)量是用速度 v （ t ） 行進(jìn)距離 D （ t ） 所需的時(shí)間。很明顯，A 到達(dá) B 當(dāng)且僅當(dāng)存在一個(gè)瞬間 t * 使得 D （ t * ） = 0 或相同的 τ （ t *） = 0。以下條件由等式 5 表示，而可達(dá)性是一個(gè)更強(qiáng)的條件，在某種意義上，除了前一個(gè)條件之外，在函數(shù) τ （t） 的有限處存在零。 順便說一句，如果正函數(shù)的唯一零在無窮遠(yuǎn)處，則相應(yīng)的成就是漸近的（即，必須經(jīng)過無窮大的時(shí)間）。如果

攻擊者不能接近最小距離。這些考慮提出了以下定義： τ （ t ） 是碰撞時(shí)間。我們注意到這個(gè)大小不能從運(yùn)動(dòng)學(xué)數(shù)據(jù)中確定。相反，它必須是先驗(yàn)的，然后才能確定我們正在建模的戰(zhàn)爭沖突的結(jié)果。根據(jù)等式 5 并考慮到等式 6，可得出：

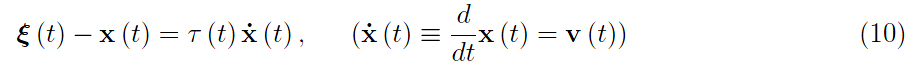
該方程可以逐個(gè)分量地寫出（根據(jù)坐標(biāo)軸 x、y、z），得到一階微分方程組：

其中，連同初始條件

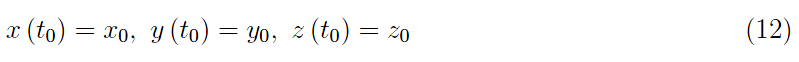
它唯一地確定了解決方案，從而確定了攻擊者的軌跡。我們稱 （11） 跟蹤方程或追蹤方程。為了在Mathematica計(jì)算環(huán)境中執(zhí)行模擬， 最好在二維中工作，抑制系統(tǒng) （11） 的第三個(gè)方程（我們將立即得出的結(jié)論推廣到通常的三維）。所以讓我們重寫：

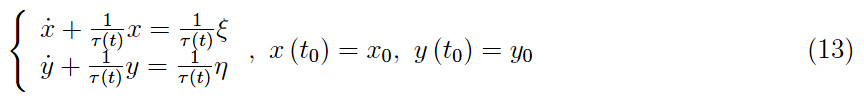
（13） 型微分方程的特點(diǎn)在于解具有初始瞬態(tài) ，然后讓位于穩(wěn)態(tài)解。換言之，在初始階段之后，追蹤軌跡經(jīng)歷了穩(wěn)定。例如，在圖 3 中，顯示了一些跟蹤幀，但沒有實(shí)現(xiàn)，因?yàn)槲覀兪褂?τ （ t ） = τ 0 》 0。由于初始條件的特定選擇，在這種情況下，沒有初始瞬態(tài)，并且跟蹤軌跡本身就是一個(gè)圓。我們觀察到存在追逐，因?yàn)楣粽叩乃俣仁噶浚ㄋ{(lán)點(diǎn)）朝向目標(biāo)的瞬時(shí)位置（紅點(diǎn)）。

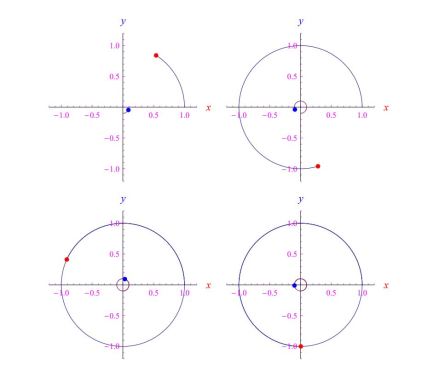
圖 3：紅點(diǎn)穿過指定的圓周，而藍(lán)點(diǎn)跟隨紅點(diǎn)，因?yàn)樗俣仁噶恐赶蚣t點(diǎn)的瞬時(shí)位置。很明顯，藍(lán)色永遠(yuǎn)不會(huì)變成紅色，因?yàn)槲覀冊(cè)O(shè)置了 τ （t） = τ0 》 0。

在圖 4 中，我們報(bào)告了一些帶有初始瞬態(tài)的追逐幀。如您所見，軌跡非常具有啟發(fā)性。我們可以假設(shè)以下類型的線性定律，而不是考慮函數(shù) τ （ t ） 相同地恒定（并且為正）：

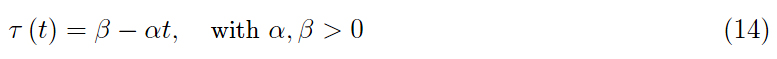
其成就時(shí)刻為 t * = β / α。 α = 10 ， β = 0的前一種情況（循環(huán) 跟蹤）。2，整合跟蹤方程，我們得到圖5的幀。在更現(xiàn)實(shí)的場(chǎng)景中，目標(biāo)以隨機(jī)模式執(zhí)行規(guī)避機(jī)動(dòng)或執(zhí)行隨機(jī)游走。眾所周知，后者是維納過程。2Mathematica 計(jì)算環(huán)境允許快速實(shí)施此過程。準(zhǔn)確地說，通過一個(gè)數(shù)組的插值，它的元素是白噪聲假定的值，我們得到一個(gè)在數(shù)學(xué)分析意義上實(shí)際上是時(shí)間函數(shù)的量。換句話說，進(jìn)入跟蹤方程 （13） 的目標(biāo)坐標(biāo)被視為通常的函數(shù)，因此可以通過 Mathematica 執(zhí)行 它們的積分，從而知道跟蹤的軌跡。在圖 6 中，我們報(bào)告了隨機(jī)游走中目標(biāo)的一些追蹤/實(shí)現(xiàn)幀，而在圖 7 中，繪制了兩架飛機(jī)的速度。目標(biāo)是清晰的白噪聲。

結(jié)論

追蹤方程（11）作用于攻擊者速度矢量的方向和方向。另一方面， 函數(shù)τ （ t ） 作用于該向量的模，即，作用于標(biāo)量函數(shù)v （ t ）。

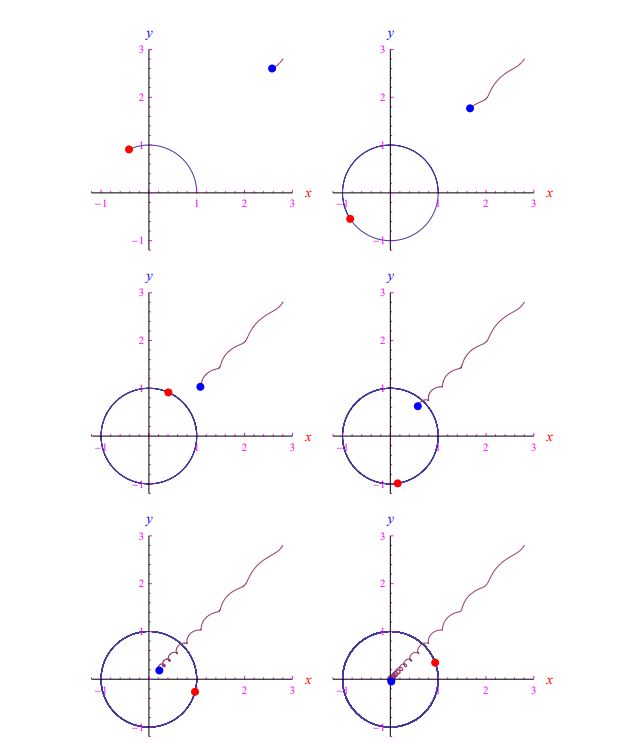
圖 4：術(shù)語“瞬態(tài)”描述了一條曲線，直到它停留在半徑 1/√401 的圓周上。

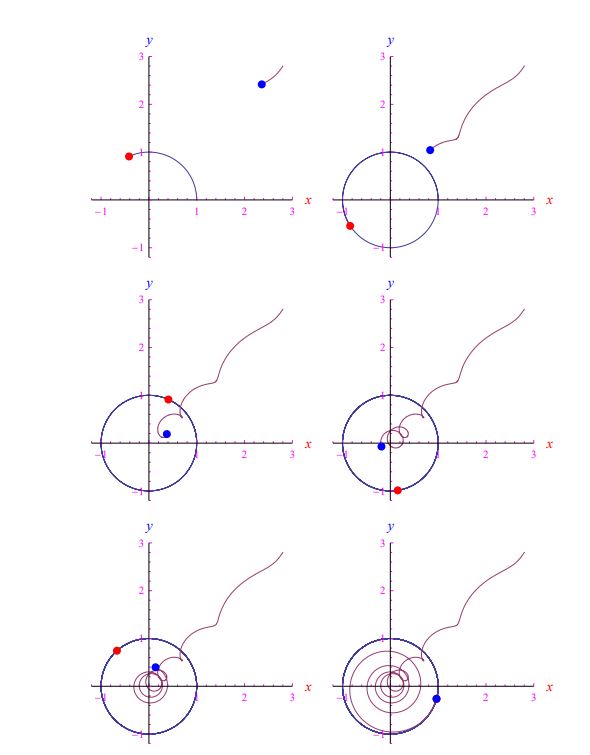
圖 5：攻擊者在時(shí)間t * = 50（無量綱單位）后到達(dá)目標(biāo)。

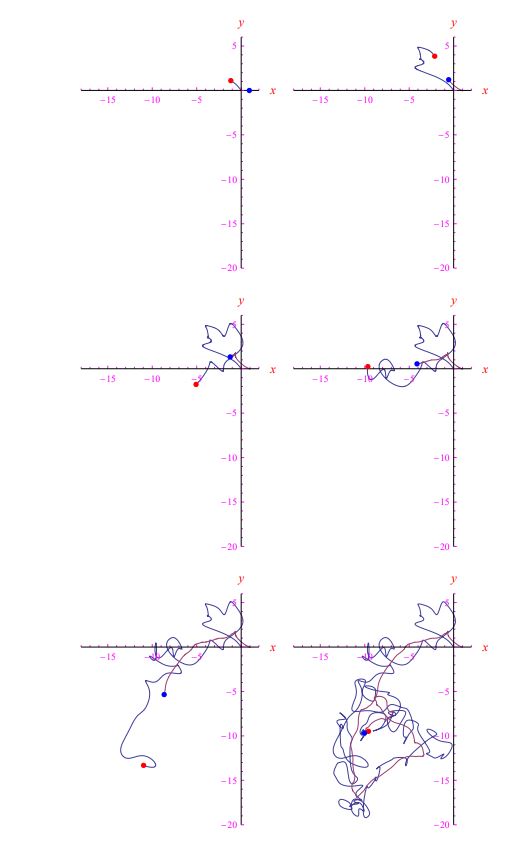
圖 6：攻擊者在時(shí)間t * = 200（無量綱單位）后到達(dá)目標(biāo)。

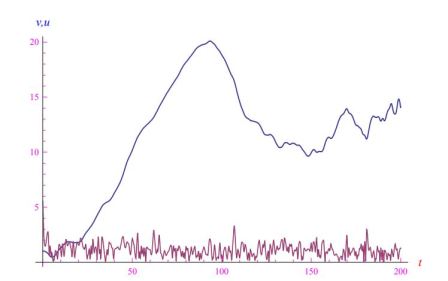
圖 7：速度與時(shí)間（無量綱單位）

由此可見，追擊是由攻擊者通過 ξ （t） 決定的，而碰撞是由 τ （t） 決定的。我們的算法是一個(gè)有趣的計(jì)算實(shí)驗(yàn)，可以更好地理解 IRST 運(yùn)動(dòng)學(xué)。

審核編輯：郭婷