(1)等副瓣電平;
(2)在相同副瓣電平和相同陣列長度下主瓣最窄,為最佳陣列;
(3)單元數過多時,陣列兩端單元激勵幅度跳變大,使饋電困難。一般在雷達系統中,為了使其具有較高的抗干擾、抗反輻射導彈的能力,往往要求雷達天線的副瓣盡量低,而采用道爾夫-切比雪夫綜合法以及進一步的泰勒綜合法等設計的陣列天線就可以實現低副瓣。最早,道爾夫(C.L.Dolph)利用切比雪夫函數來逼近天線陣列的陣因子函數,得到了這種嚴謹規范的綜合方法。而且,經過前人研究,當天線單元N≤13時,切比雪夫陣列從中間到兩端的激勵分布是單調減小的;而當N>13時,陣列兩端單元的激勵開始出現跳變。所以對于大型陣列來說一般不宜采用切比雪夫方法綜合陣列。所以下面的Matlab程序正常工作在天線單元數N為3到13這個范圍內。關于如何采用切比雪夫多項式去設計陣因子的具體技術步驟,另一篇文章較為詳細地介紹了,此處不再贅述,大家可以在文尾或評論區查看。下面是可以綜合設計天線單元從3到13單元的切比雪夫綜合法的Matlab程序:|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
|
----END 上文提到的另一篇文章。
陣列天線綜合之切比雪夫低副瓣陣列設計 MATLAB(作者:OLIVERMAHOUT)
相控陣天線中,直線陣列作為重要的一種,有著極為廣泛的應用。切比雪夫低副瓣陣列設計是一種典型的設計方法。
切比雪夫方法主要是實現低副瓣、窄波束:
其產生的核心如下:
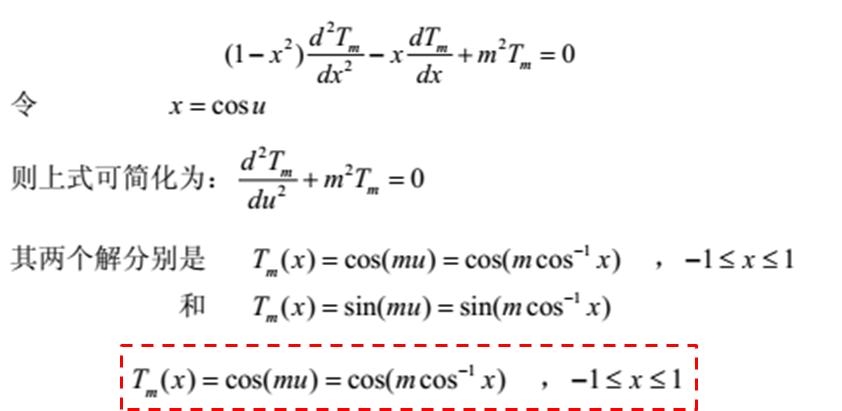
我的理解:因為能量守恒,所有副瓣都一樣的時候,能量會更多的集中在副瓣中,
主瓣最大增益也不會改變,這樣就可以使主瓣窄,副瓣電平降低。G=4πS/λ2
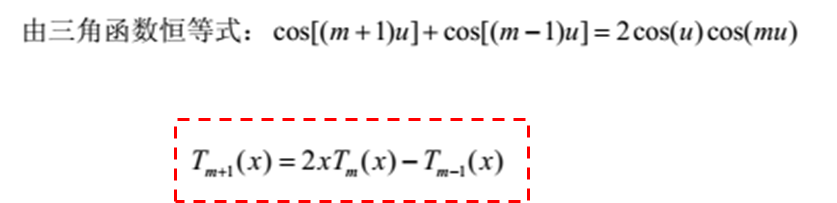
結合切比雪夫函數,可以得到:
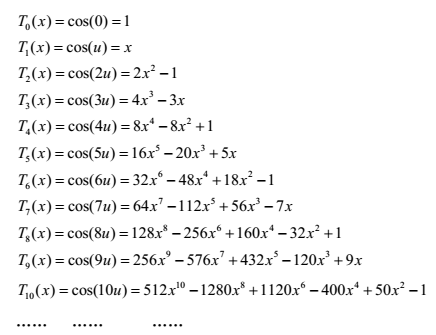
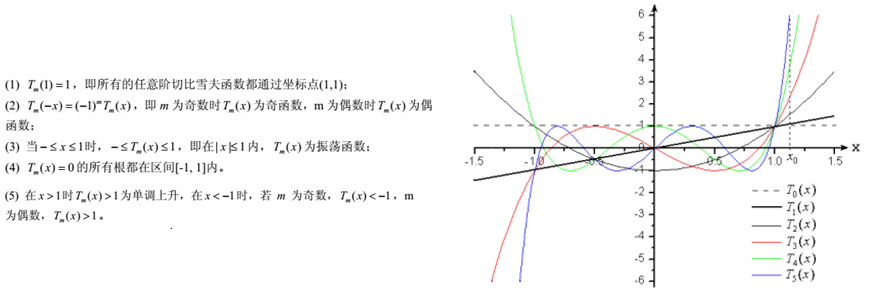

當具體應用時,解決方案如下:

話不多說,其Matlab中的程序如下:

1
% 2019-11
% 切比雪夫低副瓣陣列饋電設計_1.0 (端射陣)
close all;
clear
% digits(3);
% 參數設置
lamda = 1; % 波長
d = lamda * 0.6; % d為陣元間距
theta0 = (120/180)*pi; % 掃描角度
theta = 0: 0.01 : pi; % Θ為方向角
u = pi*d*(cos(theta)-cos(theta0))/lamda;
%T = Chebyshev; % T為切比雪夫恒等式系數矩陣
N = 10; % N為直線陣的陣元數量,M為一側的單元數(對稱)
R0dB = 26; % R0dB為副瓣電平
if (mod(N,2)==0)
M = N / 2;
parity = 0; % parity為奇偶性,0為偶數
else
M = (N+1)/2;
parity = 1;
end
% 導入切比雪夫多項式
syms x;
T = [
1;
x;
2*x^2-1;
4*x^3-3*x;
8*x^4-8*x^2+1;
16*x^5-20*x^3+5*x;
32*x^6-48*x^4+18*x^2-1;
64*x^7-112*x^5+56*x^3-7*x;
128*x^8-256*x^6+160*x^4-32*x^2+1;
256*x^9-576*x^7+432*x^5-120*x^3+9*x;
512*x^10-1280*x^8+1120*x^6-400*x^4+50*x^2-1
];
% 換算副瓣電平R0
R0 = 10 ^ (R0dB / 20);
% 計算x0
x0 = ((R0 + sqrt(R0^2 -1))^(1/(N-1)) + (R0 - sqrt(R0^2 -1))^(1/(N-1))) * 1/2;
% 定義饋電幅度矩陣I
I = sym('I', [1 M]);
% 計算展開的方向圖表達式
S = T(2) * I(1);
for k = 2 : M
S = S + T(2*k) * I(k);
end
%collect(S,x)
%vpa(S)
S_po = coeffs(S,x); % 含電流的方向圖多項式系數
T_po = sym2poly(T(N)); % 標準的方向圖多項式系數(反向了)
T_PO = zeros(1,M);
for k = 1 : M
T_PO(k) = T_po(2*k-1);
S_po(k) = S_po(k)/x0^(2*k-1);
end
% T_PO
% vpa(S_po)
% 系數比較求出電流大小
eq = sym('eq',[M 1]); % 系數比較恒等式
for k = 1 : M
eq(k) = S_po(k) == T_PO(M+1-k);
end
vpa(eq)
I_st = solve(eq);
I_ce = struct2cell(I_st);
i = zeros(M,1); % 最終的電流矩陣
for k = 1 : M
i(k) = I_ce{k,1};
i(k) = i(k);
end
for k = 2 : M
i(k) = i(k)/i(1); % 電流歸一化
end
i(1) = 1; i
i=[1;0.89;0.706;0.485;0.357]; % 用來檢驗的數據
% 計算最終的陣因子
S_all = zeros(1,length(theta));
for k = 1 : M
S_all = S_all + i(k)*cos((2*k-1)*u);
end
SS = S_all;
% 畫圖 —— 直角坐標系
S_max = max(S_all); % 歸一化處理
S_all = 20*log10(abs(S_all/S_max)); % 取分貝值
figure('NumberTitle', 'off', 'Name', 'S Parameter (dB) - Cartesian');
theta_ = theta * 180 / pi;
plot(theta_,S_all,'k','LineWidth',1.5);
grid off
xlabel(' heta (°)','FontSize',13);
ylabel('|S| dB','FontSize',12);
axis([0 182 -50 2]);
box on
% 畫圖 —— 極坐標系
figure('NumberTitle', 'off', 'Name', 'S Parameter (dB) - Polar');
S_pol = SS / max(SS);
polarplot(theta,S_all,'k','LineWidth',1.5);
thetalim([0 180]);
rmin = min(S_all);
rmax = max(S_all);
rlim([-50 rmax]);

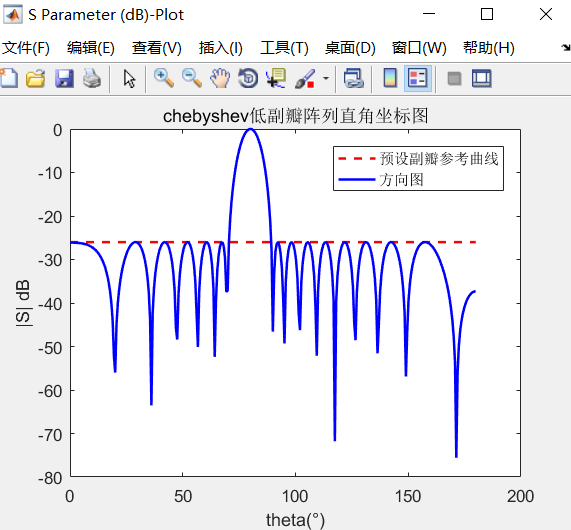
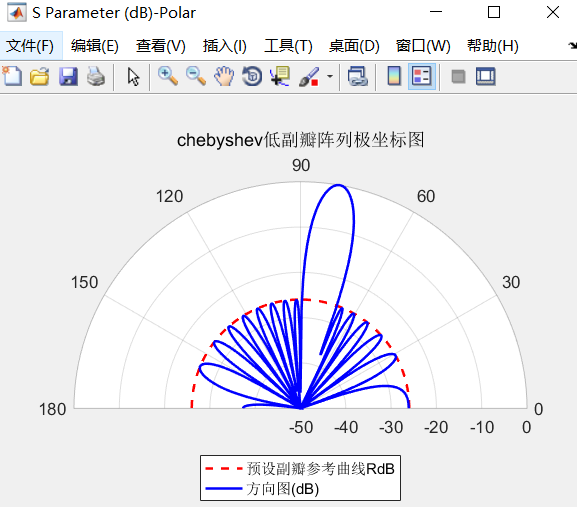
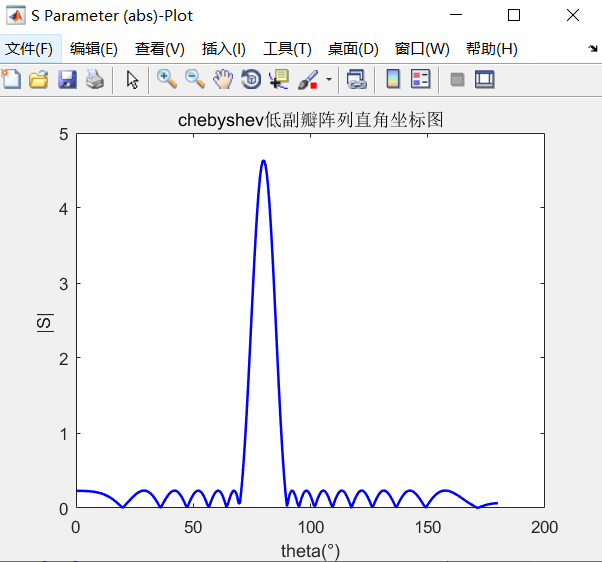
上述測試的N=10的10個陣列,側射陣(θ=0),副瓣電平SLL=26dB,結果如下:
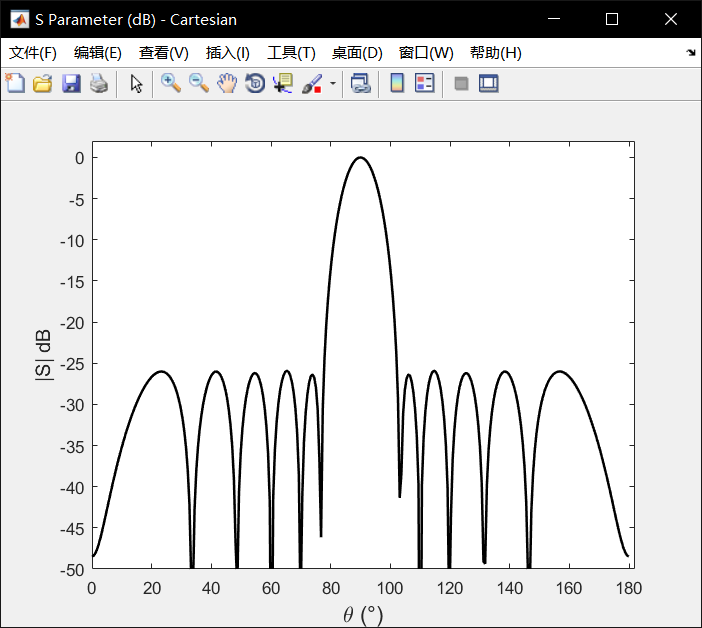
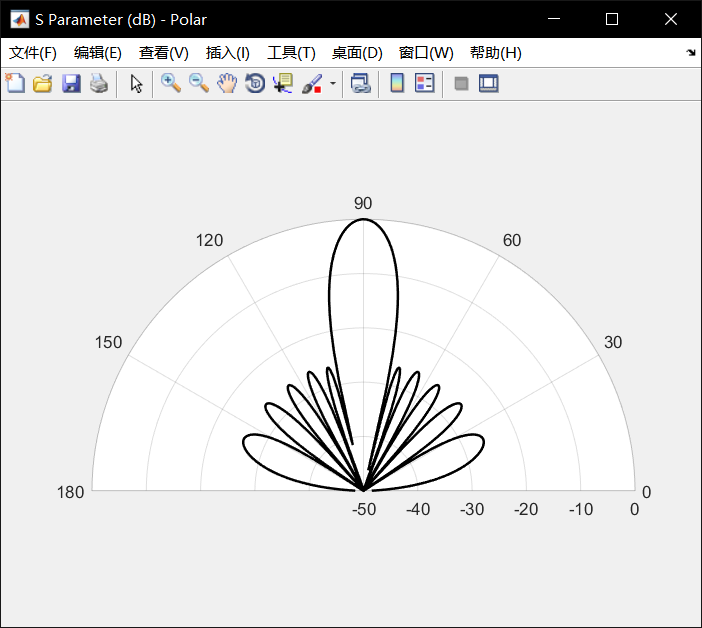
經過比較,結果較為標準。
更改一下theta0的值,改為120讀,即偏離法相30度:
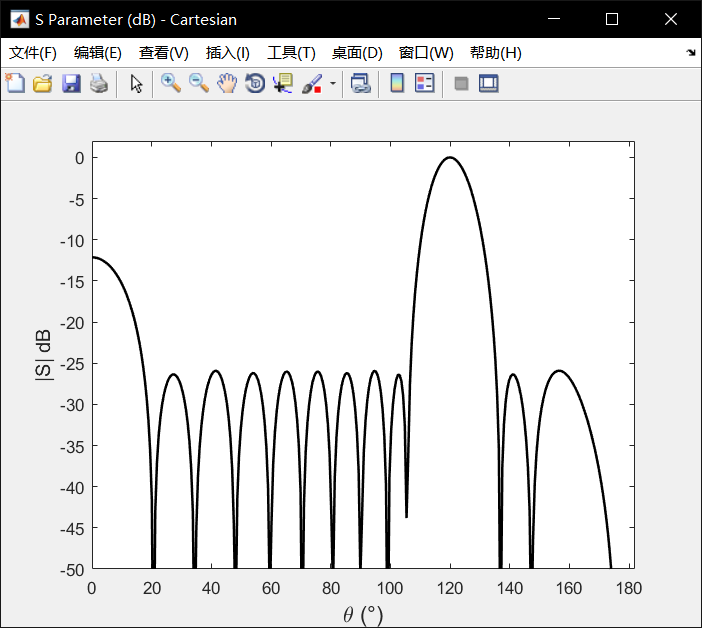
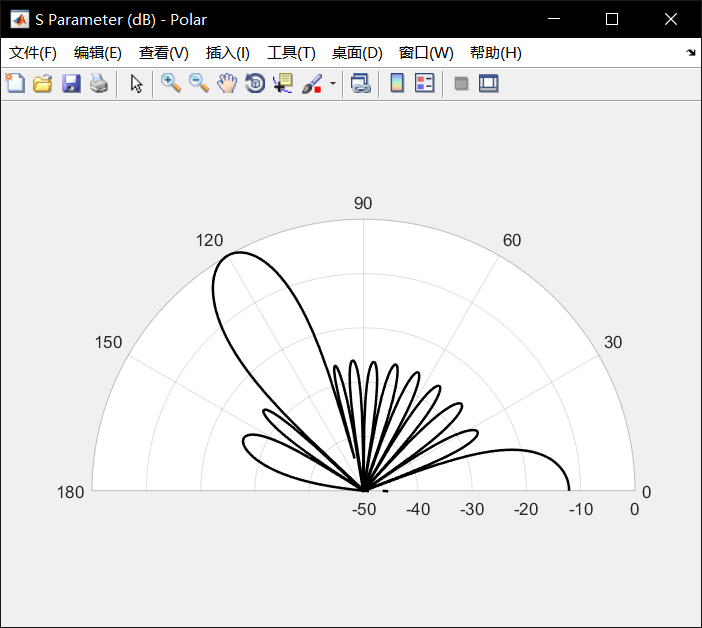
-
matlab
+關注
關注
182文章
2963瀏覽量
230170 -
電平
+關注
關注
5文章
359瀏覽量
39855 -
陣列天線
+關注
關注
3文章
33瀏覽量
10994
原文標題:MATLAB陣列天線之切比雪夫低副瓣陣列設計
文章出處:【微信號:ZGDZGCS,微信公眾號:電子萬花筒】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
使用FilterPro軟件設計的帶通濾波器和設定的差很多是為什么?
如何使用MATLAB創建預測模型
MATLAB如何使用訓練好的網絡
電力電容器手動投切和自動投切區別在哪

什么是基爾霍夫電壓定律 什么是基爾霍夫電流定律
基爾霍夫電流定律的內容和表達式 基爾霍夫電流定律的作用對象是
哈夫曼編碼怎么算 哈夫曼編碼左邊是0還是1
基爾霍夫電流定律體現了什么性質
基爾霍夫定律包括哪些定律
基爾霍夫定律與什么有關
基爾霍夫定律體現了什么守恒
霍夫變換的原理簡述





 切比雪夫綜合法的Matlab程序
切比雪夫綜合法的Matlab程序










評論