很多的CAE軟件中提供了局部網格參數功能,即可以設置幾何局部區域的網格尺寸。網格是影響仿真結果的一個主要因素,網格太稀疏,計算結果不精確,網格太密,浪費計算資源。早期軟件的仿真精度很大程度依靠工程師的經驗。
為了解決這個問題,出現了自適應網格劃分方法,其基本原理是將初始網格劃分的比較稀疏,計算一次后,找出結果梯度比較大的區域,對網格進行加密后,再進行計算,繼續找出梯度大的區域,如此反復,直到收斂到一個標準為止,該方法前面中有過介紹,參考附錄。
該方法具有通用性,但迭代計算比較耗費時間,特別對大case,在對具體行業應用時,還可以進一步優化。通常幾何模型的拓撲(即形狀,比如導彈,汽車)很少變化,所以在網格參數設置時候可以根據幾何形狀,材料類型等實際特點一步將網格參數設置到位,可以減少人為的干預。
本文介紹利用優化軟件Isight在開發行業CAE軟件中的一些經驗。(不是給Isight打廣告,而是用起來確實比較方便,在自己用過的大case中,也有isight算不出來情況)
功能:對某電子產品散熱進行模擬 (電子產品結構基本固定,由基板,芯片,蓋板組成)
目的:找到三者的最優網格大小設置。
當幾何簡單時,用戶很容易找到網格最優設置。當幾何比較復雜時,相當多用戶自己找最優解還是有一定難度的。針對如下某類型的電子產品有如下模板:
基板,蓋板各有2個,芯片4個,網格使用四面體,在軟件中設置好各部分網格的參數,讓用戶不用干預網格。
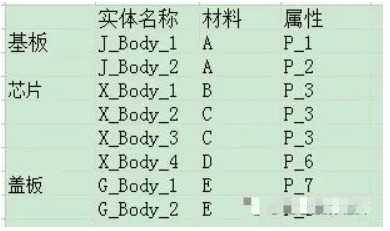
步驟:
1. 求出精確解;
2. 設置各部分網格初始參數;
3. Isight中設置優化流程;
4. Matlab提取結果,將結果返回Isight;
5. 找到各個部分網格的最佳參數;
6. 找到材料,屬性與網格參數的關系。
第6步最后會計算出網格尺寸和參數的關系表達式,這個需要大量的測試。
關于Isight軟件的介紹:
ISIGHT是美國Engineous公司出品的過程集成和優化設計的軟件,可以將數字技術、推導技術和設計探索技術有效融合,并把需要大量人工完成的工作由軟件自動化處理實現,在多學科優化軟件中的市場占有率居首位。ISIGHT軟件可以集成仿真代碼并提供設計支持,從而對多個設計可選方案進行評估研究,大大縮短了產品的設計周期,顯著提高了效率。ISIGHT在縮短產品設計周期、降低產品成本、提高產品質量等方面,取得令人矚目的突破。優化功能作為ISIGHT軟件的重要組成部分,結合ISIGHT平臺強大的集成功能和豐富多樣的優化算法庫,已成為航空航天、汽車、兵器、船舶、電子、動力、機械、教育研究等領域首選的設計優化解決方案。總的來說,ISIGHT軟件的優化功能有集成自動化、算法多樣化和結果數據可視化分析等三大優勢。
一、集成自動化
一個典型的工程需要不斷進行"設計-評估-改進"的循環。CAD和CAE的引入提高了這一過程的效率。CAD加快了造型、裝配、出圖的設計過程,CAE則減少了大量的試驗,提供了有效的分析和評估工具。但是在這種設計過程中,大多數是重復性工作,中間環節容易出錯。ISIGHT通過一種搭積木的方式快速集成各種仿真軟件,將所有設計流程組織到一個統一的框架中,自動運行仿真軟件,并自動重啟設計流程,從而消除了傳統設計流程中的"容易出錯"問題,使整個設計流程實現全數字化和全自動化。
典型的仿真優化過程主要包括以下四個步驟:
-軟件集成(集成一個或多個仿真軟件)
-問題定義(定義設計變量、約束和目標函數)
-設計自動化(選擇優化設計算法)
-數據分析和可視化(實時監控設計分析過程)
二、算法多樣化
ISIGHT提供了豐富的優化算法庫,包括數值優化算法、智能優化算法,以及處理多目標優化問題的多目標優化算法,既可處理離散變量,也可探索連續的設計空間。對于目標函數存在多峰性、非線性、不可微函數,數值優化算法可能無法尋找最優解,而全局優化算法則為解決這類問題提供了新的思路。工程上,經常出現同時對多個目標進行優化,這些目標之間是相互沖突的,因此設計人員需要對多目標進行比較,權衡,使得多個目標盡可能達到最優。ISIGHT提供了多種多目標優化算法,并支持對多目標優化的pareto圖的直觀分析。
三、結果數據可視化分析
對于大多數設計軟件,算法開始執行后需要等待算法程序結束后用戶才可以查看計算結果數據,用戶面對的好像一個"黑匣子",缺乏可視化的方法來實時監控設計過程的運行狀態。而ISIGHT軟件不但提供了多種程序結束后分析查看數據的方法,還做到了實時監控運行過程,主要體現在以下幾個方面:
1. 在優化設計過程中,提供了以圖表的形式直觀、實時地展現優化計算過程的探索狀況。
2. 多角度把握進程結束后的設計參數和目標函數的變化及相關關系,使問題的特性更加明確。
3. 提供了針對多目標設計問題專門的后處理能力,有效地查看Pareto數據,使復雜數據的分析更加簡單。
從模型可以看出,影響網格參數的有幾何的形狀,個數,材料,額外屬性,相當于每一個步長就有 8^4種組合。如此多的參數無法一一測試,只能利用DOE和優化算法來簡化計算。
在實際應用中,優化后的網格優勢很明顯:即一次可以將網格劃分成功,避免了自適應網格的反復迭代計算,在求解精度方面也滿足要求。當case 比較簡單,這種方法的優勢體現不出;如果工程師經驗足夠豐富,也能達到相同的效果。所以該方法的價值依賴于具體的行業應用。
審核編輯:劉清
-
matlab
+關注
關注
182文章
2963瀏覽量
230170 -
幾何模型
+關注
關注
0文章
4瀏覽量
6111 -
cae軟件
+關注
關注
0文章
9瀏覽量
7017
發布評論請先 登錄
相關推薦
Simcenter HEEDS設計空間探索和優化軟件

北京軟件開發公司有那些?做軟件的公司有哪些?
9月12日云技術研討會 | ECU電控軟件開發及測試全流程解決方案

如意香山筆記本軟件適配工作穩步推進,成功運行多款Linux發行版及國產辦公套件
【《軟件開發珠璣》閱讀體驗】+ 心得
名單公布!【書籍評測活動NO.33】做了50年軟件開發,總結出60條經驗教訓,每一條都太扎心!
淺談存內計算生態環境搭建以及軟件開發
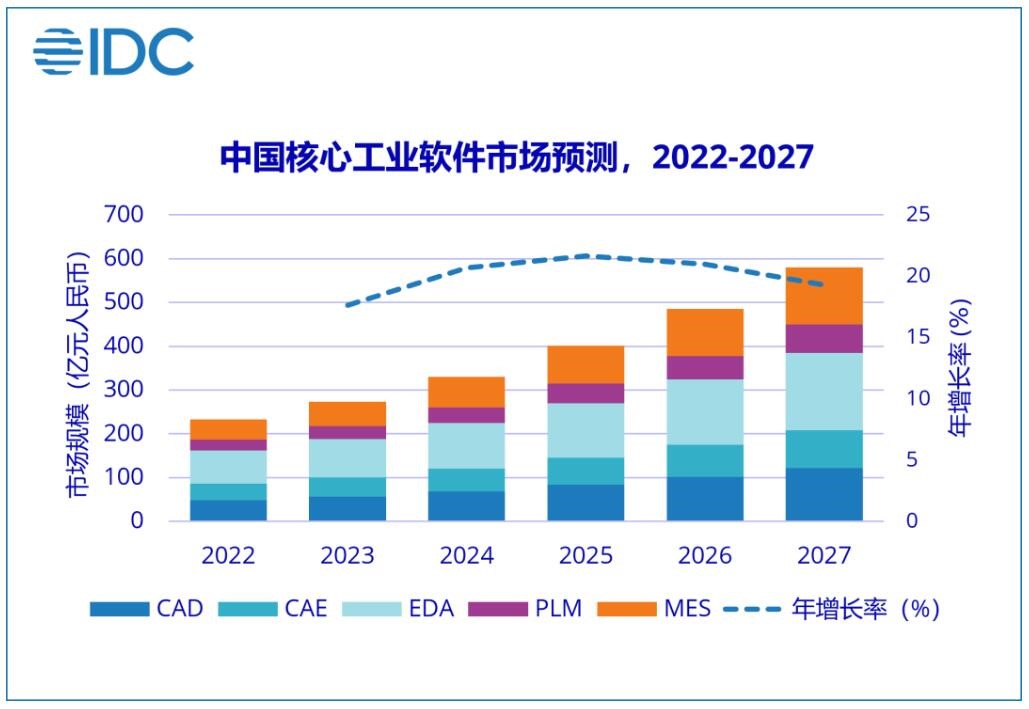
工業軟件呈現五大趨勢,國內市場加速發展




 介紹利用優化軟件Isight在開發行業CAE軟件中的一些經驗
介紹利用優化軟件Isight在開發行業CAE軟件中的一些經驗












評論