了解在直流和穩(wěn)態(tài)交流電路分析中使用 Python 和 SymPy 如何幫助加快和簡化網(wǎng)格電流和相量電流等計算。
基本電路是線性系統(tǒng),確定電路中的電流或電壓值需要使用線性代數(shù)。我發(fā)現(xiàn)當(dāng)我“求解”一個電路(即確定流過電路中所有元件的電流值)時,電路定律的應(yīng)用早在確定感興趣的數(shù)量之前就已經(jīng)完成。在短短幾分鐘內(nèi),我們就可以確定一個描述簡單電路行為的方程組。然而,手動操作這組代數(shù)方程以找到我們正在尋找的量可能需要相當(dāng)長的時間。
許多學(xué)生和教育工作者經(jīng)常求助于MATLAB來尋求線性系統(tǒng)的幫助,但Python和SymPy包也可以輕松免費地用于分析直流和穩(wěn)態(tài)交流電路。讓我們通過一些示例來說明這一點,從 DC 分析開始。
DC 分析示例 - 使用 Python 求解網(wǎng)格電流
圖 1 中的電路在現(xiàn)實生活中可能不存在,它沒有任何實際用途。
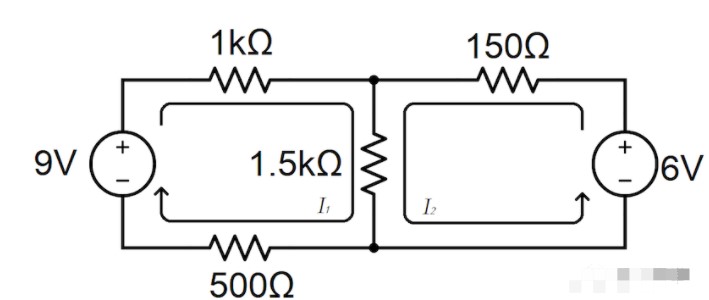
圖 1. 直流電路示例電路原理圖。
然而,在典型的電路分析教科書中,使用這種帶有直流電源的全電阻電路作為在大型電路環(huán)境中練習(xí)應(yīng)用基爾霍夫定律和歐姆定律的一種手段。
作為說明,我認(rèn)為如果您將這些不視為可能是真實的電路,而是將其視為具有特定知識基礎(chǔ)和技能組合的人的難題來解決……這會有所幫助……為了好玩!
除此之外,我已經(jīng)在該電路上繪制了網(wǎng)狀電流I 1和 I 2,我們可以使用網(wǎng)狀電流分析技術(shù)來設(shè)計以下等式 1a 和 1b:
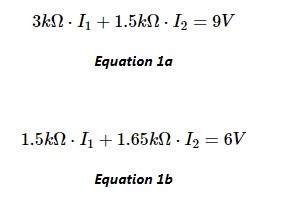
有了這個方程組,我們就有效地完成了電路理論的應(yīng)用。將這些方程一起處理以求解網(wǎng)格電流 I 1和 I 2的值的剩余任務(wù)是純代數(shù)的。讓我們將這個方程組轉(zhuǎn)換為矩陣,并使用 Python 為我們研究代數(shù),而不是手動這樣做。我們的矩陣將由每個網(wǎng)格電流的電阻系數(shù)和方程右側(cè)的電壓組成,如圖 2 所示。
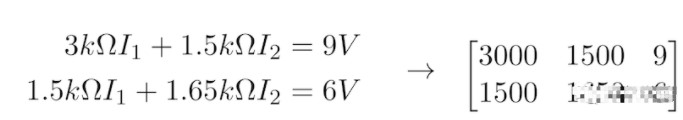
圖 2. 描述圖 1 電路的 I、R 和 V 關(guān)系的矩陣方程。
接下來,我們轉(zhuǎn)向 Python。我使用Google Colaboratory 進(jìn)行此類計算,因為它可以通過網(wǎng)絡(luò)訪問,并且我需要的所有庫都可用。但是,如果您的 Python 環(huán)境包含 SymPy 庫,您可以使用您喜歡的任何環(huán)境。
為了在 Python 中求解我們的方程組,讓我們首先導(dǎo)入 SymPy 庫,然后定義我們的矩陣,最后使用以下命令計算其簡化的行梯形,以確定兩個網(wǎng)格電流的值:
from sympy import *
dcEquations = Matrix([[3000, 1500, 9],[1500, 1650, 6]])
dcEquations.rref()
這會產(chǎn)生以下輸出:
(Matrix([
[1, 0, 13/6000],
[0, 1, 1/600]]), (0, 1))
這些代碼片段告訴我們,I 1的值為 13/6000 A 或 2.17 mA,而 I 2的值為 1/600 A 或 1.67 mA。
使用 Python 的穩(wěn)態(tài)交流分析示例
我們用于分析圖 1 中的直流電阻電路的方法也可以用于分析穩(wěn)態(tài)交流電路,并且 在紙上設(shè)計一個實際上可以服務(wù)于實際目的的交流電路并不需要花費太多精力。圖 3 顯示了一個帶有兩個無功負(fù)載(電感器)的電路,每個負(fù)載都可以代表一個用于空調(diào)單元、污水泵、冰箱壓縮機或其他家用電器設(shè)備的電機。
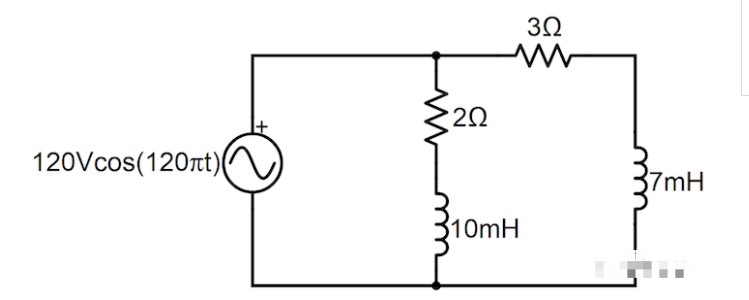
圖 3. 具有兩個無功負(fù)載的穩(wěn)態(tài)交流電路示例。
圖 3 中的電路稱為“穩(wěn)態(tài)”交流電路,因為它的電源具有固定頻率和恒定幅度。從這里開始,我們需要將電路中的電感轉(zhuǎn)換為阻抗(以歐姆為單位),以便我們可以使用網(wǎng)格電流方法來分析其穩(wěn)態(tài)行為。因此,我們根據(jù)公式 2 計算電路中電感器的阻抗,使用源的驅(qū)動頻率為 ω (120π rad/s)。
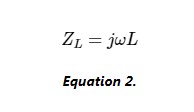
在圖 4 中,我們用每個無源元件的阻抗和相量網(wǎng)格電流 I 1和 I 2重新繪制了電路。
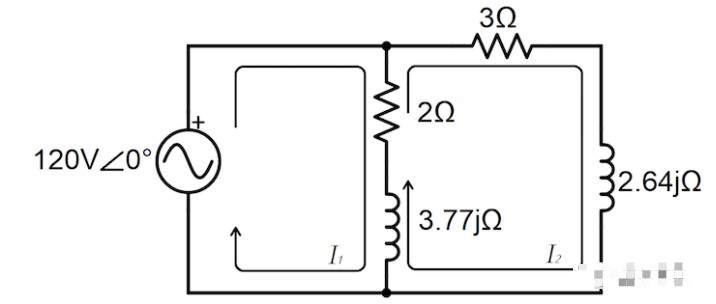
圖 4. 將電感轉(zhuǎn)換為阻抗后的圖 3 的交流電路。
就像我們對圖 1 中的電路所做的那樣,我們可以使用基爾霍夫電壓定律和歐姆定律推導(dǎo)出與圖 4 中電路中的元件和網(wǎng)格電流相關(guān)的方程組。方程 3a 和 3b 構(gòu)成了該系統(tǒng)。
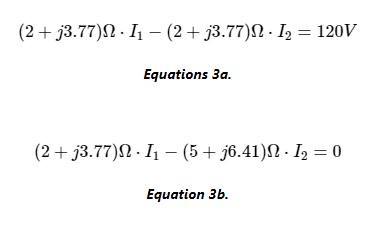
同樣,用于求解圖 4 電路中網(wǎng)格電流的其余過程是純代數(shù)。該方程組的矩陣形式如圖 5 所示。
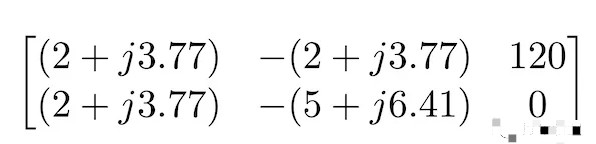
圖 5. 等式 3a 和 3b 的矩陣表示圖 4 的穩(wěn)態(tài)交流電路。
Python 中的以下命令將為圖 4 中電路中的網(wǎng)格電流值求解該方程組。請注意,我們可以在矩陣定義中使用“j”而無需任何特殊努力,因為“j”在 SymPy 中定義為復(fù)空間中的虛單位。
from sympy import *
acEquations = Matrix([[2+3.77j,-(2+3.77j), 120],[2+3.77j, -(5+6.41j), 0]])
acEquations.rref()
這會產(chǎn)生以下輸出:
(Matrix([
[1, 0, 35.7203044893402 - 44.6772284258869*I],
[0, 1, 22.5428313796213 - 19.8376916140667*I]]), (0, 1))
這告訴我們相量電流 I 1和 I 2分別為 (35.72 – j44.68)A 和 (22.54 – j19.84)A。請注意 Python 如何將虛數(shù)單位表示為“I”而不是“j”。為了將這些轉(zhuǎn)換為時間相關(guān)函數(shù),我們應(yīng)用了一點三角函數(shù)來找到它們各自的幅度和相位。I 1的幅度和相位通過等式 4a 和 4b 求得:
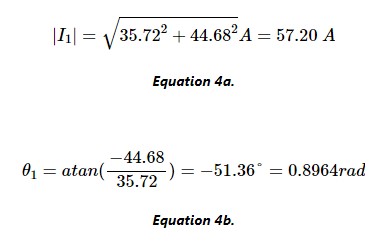
類似地,根據(jù)等式 5a 和 5b 求出I 2的幅度和相位:
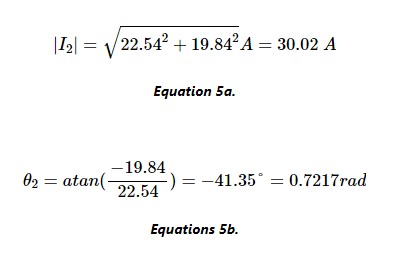
最后,給定這些幅度和相位,我們確定 I 1和 I 2的函數(shù)形式:

Python 和 SymPy 對直流和穩(wěn)態(tài)交流分析的好處
請注意,穩(wěn)態(tài)交流分析確實需要預(yù)先從電感(和/或電容)轉(zhuǎn)換為復(fù)阻抗以及之后從相量形式轉(zhuǎn)換為時間相關(guān)形式的額外步驟。然而,使用 Python 應(yīng)用這種矩陣技術(shù)在求解交流電路時比直流電路為我們節(jié)省了更多的計算時間,因為 Python 甚至可以為我們處理復(fù)雜的代數(shù),輕松處理增加的虛數(shù)維度。
對于直流和穩(wěn)態(tài)交流電路分析,可以輕松使用 Python 和 SymPy 庫來減少確定所需值所需的工作量。雖然這些示例中分析的電路相對簡單,但該技術(shù)可以擴展到具有更多網(wǎng)格的更復(fù)雜電路。以這種方式使用 Python 不僅可以減少解決電路問題所花費的時間,而且還可以幫助學(xué)生在練習(xí)新學(xué)習(xí)的網(wǎng)絡(luò)分析技術(shù)時在心理上區(qū)分電路理論和純代數(shù)。
-
DC
+關(guān)注
關(guān)注
9文章
3632瀏覽量
679349 -
交流電路
+關(guān)注
關(guān)注
0文章
182瀏覽量
28811 -
python
+關(guān)注
關(guān)注
56文章
4782瀏覽量
84456
發(fā)布評論請先 登錄
相關(guān)推薦
如下電流檢測電路具體是怎么分析的?
matlab的根軌跡、增益選擇、方程求解和演示示例命令
電源網(wǎng)格的電壓下降和電遷移(EMI)效應(yīng)分析
用網(wǎng)格鋪銅時線寬報錯,改了網(wǎng)格線寬也沒用
HFSS求解器的主要特點
網(wǎng)格電流分析電路
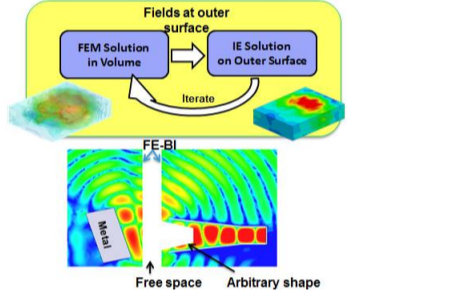
IE和FEBI求解器詳解及對比

python代碼示例之基于Python的日歷api調(diào)用代碼實例
HFSS的IE和FEBI求解器的詳細(xì)資料概述




 DC分析示例-使用Python求解網(wǎng)格電流
DC分析示例-使用Python求解網(wǎng)格電流











評論