最近讀者群里有個讀者跟我私信，說去面試微軟遇到了一系列和數學相關的算法題，直接懵圈了。我看了下題目，發現這些題其實就是 LeetCode 上面「丑數」系列問題的修改版。

首先，「丑數」系列問題屬于會者不難難者不會的類型，因為會用到些數學定理嘛，如果沒有專門學過，靠自己恐怕是想不出來的。

另外，這類問題而且非常考察抽象聯想能力，因為它除了數學定理之外，還需要你把題目抽象成鏈表相關的題目運用雙指針技巧，或者抽象成數組相關的題目運用二分搜索技巧。

那么今天我就來用一篇文章把所有丑數相關的問題一網打盡，看看這類問題能夠如何變化，應該如何解決。

丑數 I

首先是力扣第 263 題「丑數」，題目給你輸入一個數字n，請你判斷n是否為「丑數」。所謂「丑數」，就是只包含質因數2、3和5的正整數。

函數簽名如下：

booleanisUgly(intn)

比如 12 = 2 x 2 x 3 就是一個丑數，而 42 = 2 x 3 x 7 就不是一個丑數。

這道題其實非常簡單，前提是你知道算術基本定理（正整數唯一分解定理）：

任意一個大于 1 的自然數，要么它本身就是質數，要么它可以分解為若干質數的乘積。

既然任意一個大于一的正整數都可以分解成若干質數的乘積，那么丑數也可以被分解成若干質數的乘積，且這些質數只能是 2, 3 或 5。

有了這個思路，就可以實現isUgly函數了：

publicbooleanisUgly(intn){
if(n<=?0)returnfalse;
//如果n是丑數，分解因子應該只有2,3,5
while(n%2==0)n/=2;
while(n%3==0)n/=3;
while(n%5==0)n/=5;
//如果能夠成功分解，說明是丑數
returnn==1;
}

丑數 II

接下來提升難度，看下力扣第 264 題「丑數 II」，現在題目不是讓你判斷一個數是不是丑數，而是給你輸入一個n，讓你計算第n個丑數是多少，函數簽名如下：

intnthUglyNumber(intn)

比如輸入n = 10，函數應該返回 12，因為從小到大的丑數序列為1, 2, 3, 4, 5, 6, 8, 9, 10, 12，第 10 個丑數是 12（注意我們把 1 也算作一個丑數）。

這道題很精妙，你看著它好像是道數學題，實際上它卻是一個合并多個有序鏈表的問題，同時用到了篩選素數的思路。

首先，我在前文如何高效尋找質數中也講過高效篩選質數的「篩數法」：一個質數和除 1 以外的其他數字的乘積一定不是質數，把這些數字篩掉，剩下的就是質數。

Wikipedia 的這幅圖很形象：

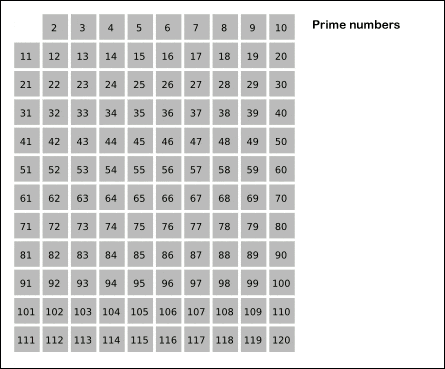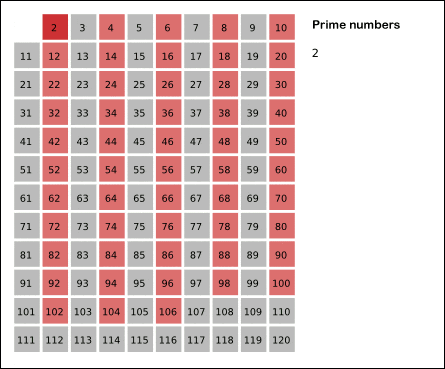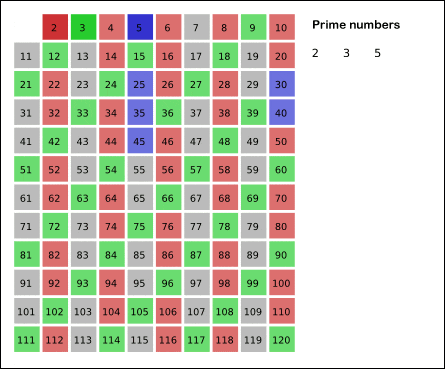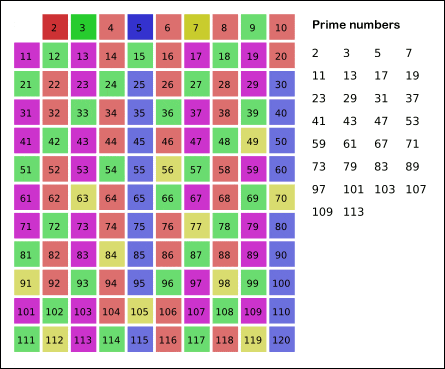
基于篩數法的思路和丑數的定義，我們不難想到這樣一個規律：如果一個數x是丑數，那么x * 2, x * 3, x * 5都一定是丑數。

如果我們把所有丑數想象成一個從小到大排序的鏈表，就是這個樣子：

1->2->3->4->5->6->8->...

然后，我們可以把丑數分為三類：2 的倍數、3 的倍數、5 的倍數。這三類丑數就好像三條有序鏈表，如下：

能被 2 整除的丑數：

1*2->2*2->3*2->4*2->5*2->6*2->8*2->...

能被 3 整除的丑數：

1*3->2*3->3*3->4*3->5*3->6*3->8*3->...

能被 5 整除的丑數：

1*5->2*5->3*5->4*5->5*5->6*5->8*5->...

我們如果把這三條「有序鏈表」合并在一起并去重，得到的就是丑數的序列，其中第n個元素就是題目想要的答案：

1->1*2->1*3->2*2->1*5->3*2->4*2->...

所以這里就和鏈表雙指針技巧匯總中講到的合并兩條有序鏈表的思路基本一樣了，先看下合并有序鏈表的核心解法代碼：

ListNodemergeTwoLists(ListNodel1,ListNodel2){
//虛擬頭結點存儲結果鏈表，p指針指向結果鏈表
ListNodedummy=newListNode(-1),p=dummy;
//p1,p2分別在兩條有序鏈表上
ListNodep1=l1,p2=l2;

while(p1!=null&&p2!=null){
//比較p1和p2兩個指針
//將值較小的的節點接到結果鏈表
if(p1.val>p2.val){
p.next=p2;
p2=p2.next;
}else{
p.next=p1;
p1=p1.next;
}
//p指針不斷前進
p=p.next;
}
//省略部分非核心代碼...
}

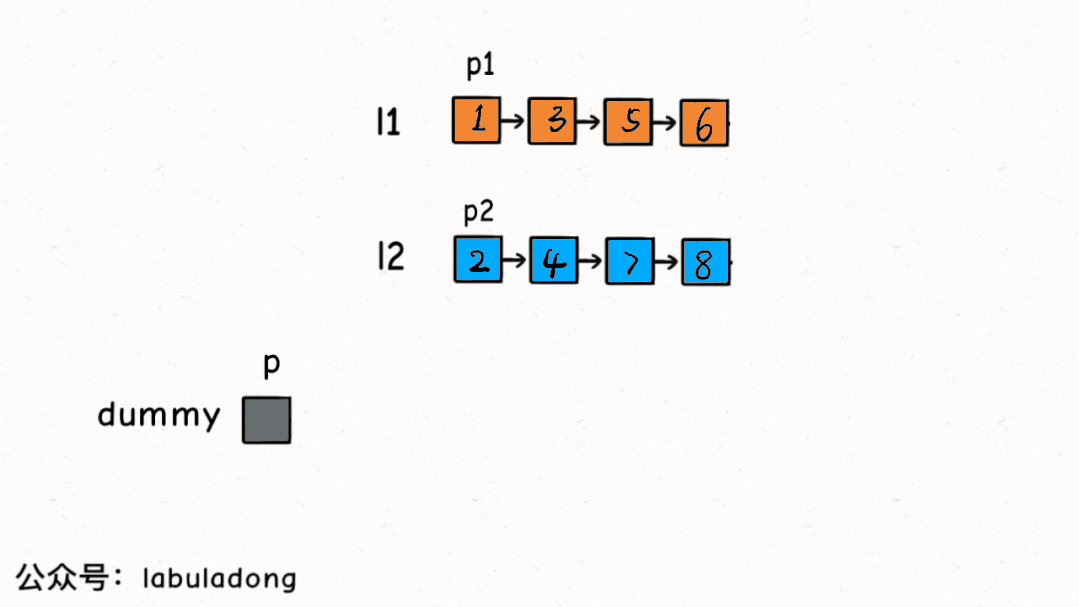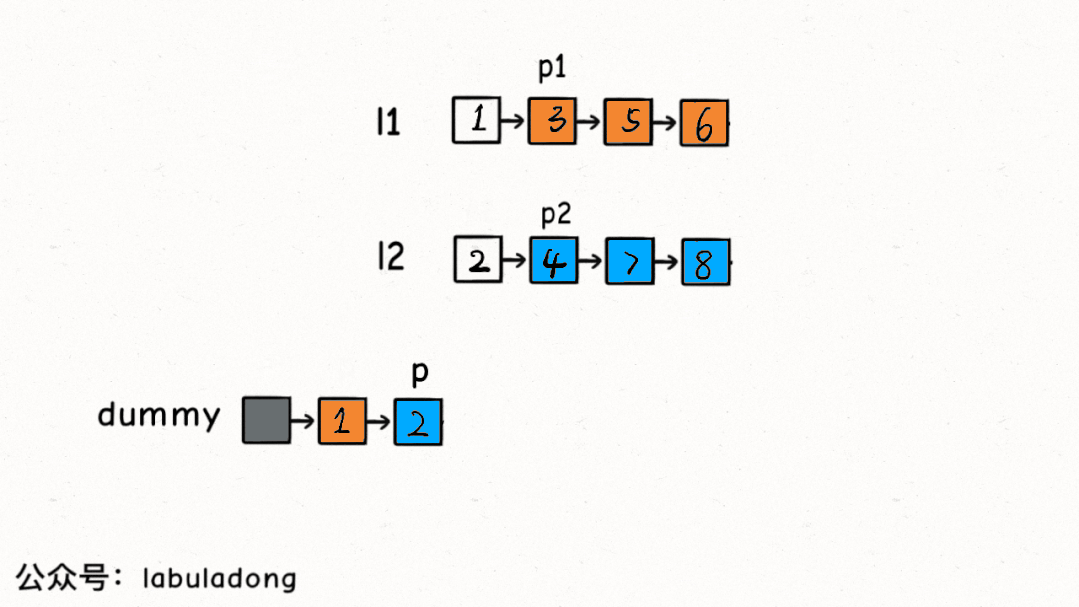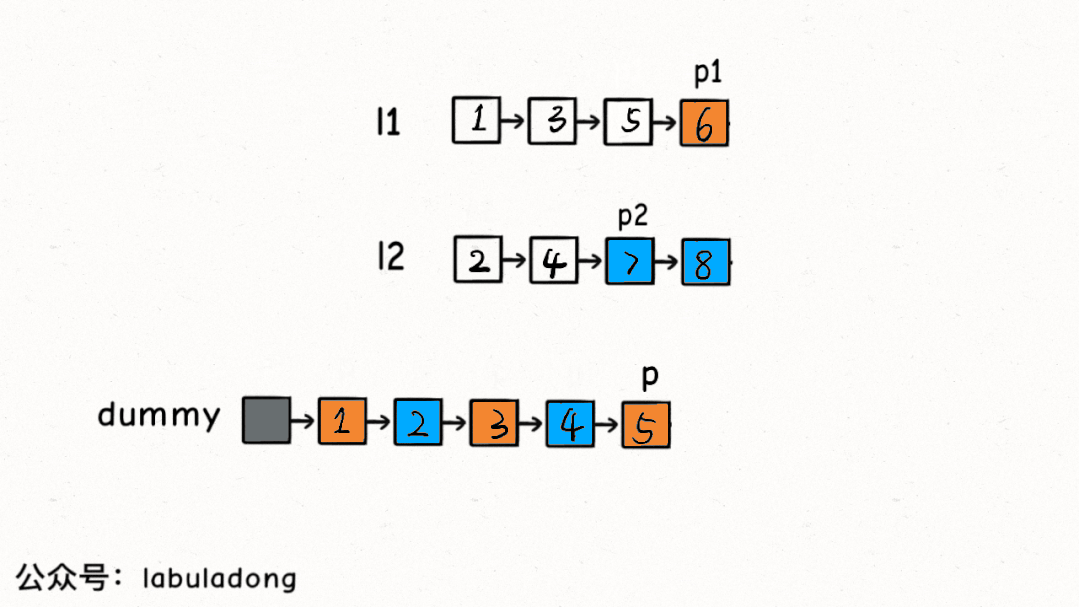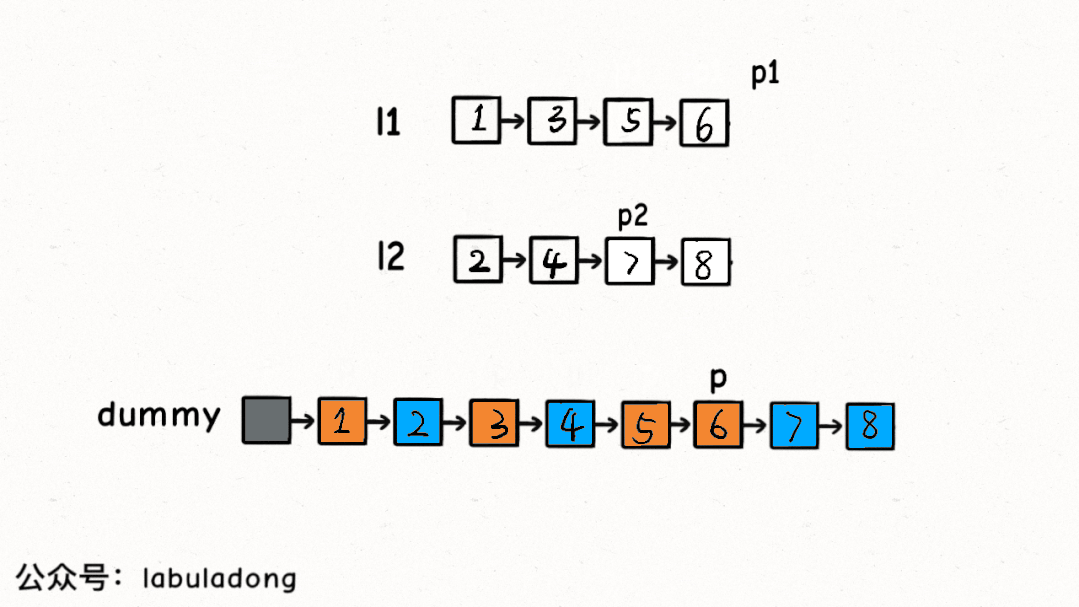
對于這道題，我們抽象出三條有序的丑數鏈表，合并這三條有序鏈表得到的結果就是丑數序列，其中第n個丑數就是題目想要的答案。

類比合并兩個有序鏈表，看下這道題的解法代碼：

intnthUglyNumber(intn){
//可以理解為三個指向有序鏈表頭結點的指針
intp2=1,p3=1,p5=1;
//可以理解為三個有序鏈表的頭節點的值
intproduct2=1,product3=1,product5=1;
//可以理解為最終合并的有序鏈表（結果鏈表）
int[]ugly=newint[n+1];
//可以理解為結果鏈表上的指針
intp=1;

//開始合并三個有序鏈表，找到第n個丑數時結束
while(p<=?n)?{
????????//取三個鏈表的最小結點
intmin=Math.min(Math.min(product2,product3),product5);
//將最小節點接到結果鏈表上
ugly[p]=min;
p++;
//前進對應有序鏈表上的指針
if(min==product2){
product2=2*ugly[p2];
p2++;
}
if(min==product3){
product3=3*ugly[p3];
p3++;
}
if(min==product5){
product5=5*ugly[p5];
p5++;
}
}
//返回第n個丑數
returnugly[n];
}

我們用p2, p3, p5分別代表三條丑數鏈表上的指針，用product2, product3, product5代表丑數鏈表上節點的值，用ugly數組記錄有序鏈表合并之后的結果。

有了之前的鋪墊和類比，你應該很容易看懂這道題的思路了，接下來我們再提高一點難度。

超級丑數

看下力扣第 313 題「超級丑數」，這道題給你輸入一個質數列表primes和一個正整數n，請你計算第n個「超級丑數」。所謂超級丑數是一個所有質因數都出現在primes中的正整數，函數簽名如下：

int nthSuperUglyNumber(intn,int[]primes)

如果讓primes = [2, 3, 5]就是上道題，所以這道題是上道題的進階版。

不過思路還是類似的，你還是把每個質因子看做一條有序鏈表，上道題相當于讓你合并三條有序鏈表，而這道題相當于讓你合并len(primes)條有序鏈表，也就是雙指針技巧秒殺七道鏈表題目中講過的「合并 K 條有序鏈表」的思路。

注意我們在上道題抽象出了三條鏈表，需要p2, p3, p5作為三條有序鏈表上的指針，同時需要product2, product3, product5記錄指針所指節點的值，每次循環用min函數計算最小頭結點。

這道題相當于輸入了len(primes)條有序鏈表，我們不能用min函數計算最小頭結點了，而是要用優先級隊列來計算最小頭結點，同時依然要維護鏈表指針、指針所指節點的值，我們可以用一個三元組來保存這些信息。

你結合雙指針技巧秒殺七道鏈表題目合并 K 條有序鏈表的思路就能理解這道題的解法：

intnthSuperUglyNumber(intn,int[]primes){
//優先隊列中裝三元組int[]{product,prime,pi}
//其中product代表鏈表節點的值，prime是計算下一個節點所需的質數因子，pi代表鏈表上的指針
PriorityQueue<int[]>pq=newPriorityQueue<>((a,b)->{
//優先級隊列按照節點的值排序
returna[0]-b[0];
});

//把多條鏈表的頭結點加入優先級隊列
for(inti=0;inewint[]{1,primes[i],1});
}

//可以理解為最終合并的有序鏈表（結果鏈表）
int[]ugly=newint[n+1];
//可以理解為結果鏈表上的指針
intp=1;

while(p<=?n)?{
????????//取三個鏈表的最小結點
int[]pair=pq.poll();
intproduct=pair[0];
intprime=pair[1];
intindex=pair[2];

//避免結果鏈表出現重復元素
if(product!=ugly[p-1]){
//接到結果鏈表上
ugly[p]=product;
p++;
}

//生成下一個節點加入優先級隊列
int[]nextPair=newint[]{ugly[index]*prime,prime,index+1};
pq.offer(nextPair);
}
returnugly[n];
}

接下來看下第四道丑數題目，也是今天的壓軸題。

丑數 III

這是力扣第 1201 題「丑數 III」，看下題目：

給你四個整數：n, a, b, c，請你設計一個算法來找出第n個丑數。其中丑數是可以被a或b或c整除的正整數。

這道題和之前題目的不同之處在于它改變了「丑數」的定義，只要一個正整數x存在a, b, c中的任何一個因子，那么x就是丑數。

比如輸入n = 7, a = 3, b = 4, c = 5，那么算法輸出 10，因為符合條件的丑數序列為3, 4, 5, 6, 8, 9, 10, ...，其中第 7 個數字是 10。

有了之前幾道題的鋪墊，你肯定可以想到把a, b, c的倍數抽象成三條有序鏈表：

1*3->2*3->3*3->4*3->5*3->6*3->7*3->...
1*4->2*4->3*4->4*4->5*4->6*4->7*4->...
1*5->2*5->3*5->4*5->5*5->6*5->7*5->...

然后將這三條鏈表合并成一條有序鏈表并去除重復元素，這樣合并后的鏈表元素就是丑數序列，我們從中找到第n個元素即可：

1*3->1*4->1*5->2*3->2*4->3*3->2*5->...

有了這個思路，可以直接寫出代碼：

publicintnthUglyNumber(intn,inta,intb,intc){
//可以理解為三個有序鏈表的頭結點的值
//由于數據規模較大，用long類型
longproductA=a,productB=b,productC=c;
//可以理解為合并之后的有序鏈表上的指針
intp=1;

longmin=-666;

//開始合并三個有序鏈表，獲取第n個節點的值
while(p<=?n)?{
????????//取三個鏈表的最小結點
min=Math.min(Math.min(productA,productB),productC);
p++;
//前進最小結點對應鏈表的指針
if(min==productA){
productA+=a;
}
if(min==productB){
productB+=b;
}
if(min==productC){
productC+=c;
}
}
return(int)min;
}

這個思路應該是非常簡單的，但是提交之后并不能通過所有測試用例，會超時。

注意題目給的數據范圍非常大，a, b, c, n的大小可以達到 10^9，所以即便上述算法的時間復雜度是O(n)，也是相對比較耗時的，應該有更好的思路能夠進一步降低時間復雜度。

這道題的正確解法難度比較大，難點在于你要把一些數學知識和二分搜索技巧結合起來才能高效解決這個問題。

首先，我們可以定義一個單調遞增的函數f：

f(num, a, b, c)計算[1..num]中，能夠整除a或b或c的數字的個數，顯然函數f的返回值是隨著num的增加而增加的（單調遞增）。

題目讓我們求第n個能夠整除a或b或c的數字是什么，也就是說我們要找到一個最小的num，使得f(num, a, b, c) == n。

這個num就是第n個能夠整除a或b或c的數字。

根據二分查找的實際運用給出的思路模板，我們得到一個單調函數f，想求參數num的最小值，就可以運用搜索左側邊界的二分查找算法了：

intnthUglyNumber(intn,inta,intb,intc){
//題目說本題結果在[1,2*10^9]范圍內，
//所以就按照這個范圍初始化兩端都閉的搜索區間
intleft=1,right=(int)2e9;
//搜索左側邊界的二分搜索
while(left<=?right)?{
????????intmid=left+(right-left)/2;
if(f(mid,a,b,c)//[1..mid]中符合條件的元素個數不足n，所以目標在右半邊
left=mid+1;
}else{
//[1..mid]中符合條件的元素個數大于n，所以目標在左半邊
right=mid-1;
}
}
returnleft;
}

//函數f是一個單調函數
//計算[1..num]之間有多少個能夠被a或b或c整除的數字
longf(intnum,inta,intb,intc){
//下文實現
}

搜索左側邊界的二分搜索代碼模板在二分查找框架詳解中講過，沒啥可說的，關鍵說一下函數f怎么實現，這里面涉及容斥原理以及最小公因數、最小公倍數的計算方法。

首先，我把[1..num]中能夠整除a的數字歸為集合A，能夠整除b的數字歸為集合B，能夠整除c的數字歸為集合C，那么len(A) = num / a, len(B) = num / b, len(C) = num / c，這個很好理解。

但是f(num, a, b, c)的值肯定不是num / a + num / b + num / c這么簡單，因為你注意有些數字可能可以被a, b, c中的兩個數或三個數同時整除，如下圖：

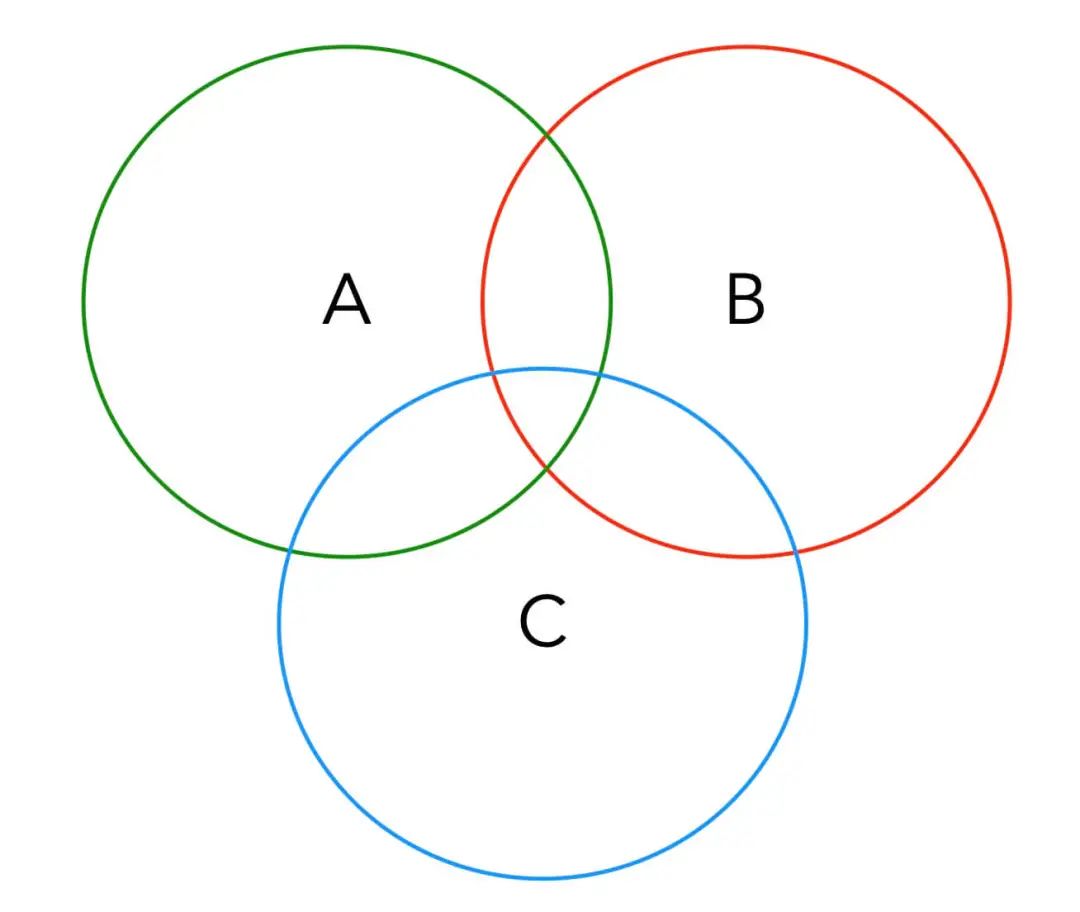
按照容斥原理，這個集合中的元素應該是：A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C。結合上圖應該很好理解。

問題來了，A, B, C三個集合的元素個數我們已經算出來了，但如何計算像A ∩ B這種交集的元素個數呢？

其實也很容易想明白，A ∩ B的元素個數就是num / lcm(a, b)，其中lcm是計算最小公倍數（Least Common Multiple）的函數。

類似的，A ∩ B ∩ C的元素個數就是num / lcm(lcm(a, b), c)的值。

現在的問題是，最小公倍數怎么求？

直接記住定理吧：lcm(a, b) = a * b / gcd(a, b)，其中gcd是計算最大公因數（Greatest Common Divisor）的函數。

現在的問題是，最大公因數怎么求？這應該是經典算法了，我們一般叫輾轉相除算法（或者歐幾里得算法）。

好了，套娃終于套完了，我們可以把上述思路翻譯成代碼就可以實現f函數，注意本題數據規模比較大，有時候需要用long類型防止int溢出：

//計算最大公因數（輾轉相除/歐幾里得算法）
longgcd(longa,longb){
if(a//保證a>b
returngcd(b,a);
}
if(b==0){
returna;
}
returngcd(b,a%b);
}

//最小公倍數
longlcm(longa,longb){
//最小公倍數就是乘積除以最大公因數
returna*b/gcd(a,b);
}

//計算[1..num]之間有多少個能夠被a或b或c整除的數字
longf(intnum,inta,intb,intc){
longsetA=num/a,setB=num/b,setC=num/c;
longsetAB=num/lcm(a,b);
longsetAC=num/lcm(a,c);
longsetBC=num/lcm(b,c);
longsetABC=num/lcm(lcm(a,b),c);
//集合論定理：A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C
returnsetA+setB+setC-setAB-setAC-setBC+setABC;
}

實現了f函數，結合之前的二分搜索模板，時間復雜度下降到對數級別，即可高效解決這道題目了。

以上就是所有「丑數」相關的題目，用到的知識點有算術基本定理、容斥原理、輾轉相除法、鏈表雙指針合并有序鏈表、二分搜索模板等等。

如果沒做過類似的題目可能很難想出來，但只要做過，也就手到擒來了。所以我說這種數學問題屬于會者不難，難者不會的類型。

審核編輯：湯梓紅