提到回溯算法那肯定離不開 n 皇后這道算法題,它實在是太經典了。
所謂n 皇后問題,指的是如何將n個皇后放置在n×n的棋盤上,并且使皇后彼此之間不能相互攻擊。
皇后彼此不能相互攻擊,也就是說:任何兩個皇后都不能處于同一條橫行、縱行或斜線上。
給你一個整數n,返回所有不同的n 皇后問題的解決方案。
每一種解法包含一個不同的n 皇后問題的棋子放置方案,該方案中'Q'和'.'分別代表了皇后和空位。
輸入:n = 4
輸出:[[".Q..","...Q","Q...","..Q."],
["..Q.","Q...","...Q",".Q.."]]
解釋:4 皇后問題存在兩個不同的解法。
我覺得你應該能夠結合視頻動畫和保姆級別的代碼注釋把這道題目弄清楚。
classSolution{
//保存所有符合要求的解
List>res=newArrayList<>();
publicList>solveNQueens(intn){
//attack用來表示皇后的攻擊范圍
int[][]attack=newint[n][n];
//queen用來記錄皇后的位置
char[][]queen=newchar[n][n];
//初始化二維數組queen中所有的元素為'.'
for(char[]c:queen){
Arrays.fill(c,'.');
}
//初始化二維數組attack中所有的元素為0
//0代表沒有皇后能攻擊得到
//1代表出于任意一個皇后的攻擊范圍內
for(int[]c:attack){
Arrays.fill(c,0);
}
//從棋盤的第0行第0列處理n皇后的情況
backtrack(0,n,queen,attack);
//最后,返回所有符合要求的解
returnres;
}
//很顯然,每一行只能放置一個皇后,所以我們每一行每一行的來放置皇后
//k表示當前處理的行
//n表示需要放置多少個皇后,同時也代表棋盤的大小為n*n
//queen用來記錄皇后的位置
//attack用來表示皇后的攻擊范圍
privatevoidbacktrack(intk,intn,char[][]queen,int[][]attack){
//如果發現在棋盤的最后一行放置好了皇后,那么就說明找到了一組符合要求的解
if(k==n){
//由于queen為二維字符數組,所以需要轉換為字符串數組
Listlist=newArrayList<>();
//遍歷二維數組queen
//取出queen的每一行字符數組c
for(char[]c:queen){
//把字符數組c中的所有字符轉換為字符串的形式進行拼湊
//比如['.','Q','.','.',]
//轉換為'.Q..'
//把這個字符串加入到list中
list.add(String.copyValueOf(c));
}
//list即為一組符合要求的解,把它加入到結果數組中
res.add(list);
//由于遍歷完了所有的行,無需再遍歷下去,所以返回
return;
}
//每一行只能放置一個皇后
//并且每一列也只能放置一個皇后
//所以在k行中,從0列到n-1列,判斷皇后應該放置到哪個位置
for(inti=0;i//如果發現attack[k][i]==0
//說明這個位置不在任何一個皇后的攻擊范圍內
//所以可以考慮放置皇后
if(attack[k][i]==0){
//如果在(k,i)位置放置了皇后,那么就需要考慮在k+1行應該怎么放置其它的皇后了
//由于有可能在(k,i)位置放置了皇后之后,在后續的其它行會無法再放置其它的皇后
//那么就需要回到(k,i)的狀態,考慮能不能在(k,i+1)的位置放置
//為了能夠回到(k,i)的狀態,所以需要先記錄此時的attack
//使用一個臨時的二維數組,深度拷貝attack
//如果不使用深度拷貝,而是直接使用int[][]temp=c
//會導致attack發生改變是temp也會發生改變
//這樣也就無法保存之前的狀態了
int[][]temp=newint[n][n];
//通過兩個for循環,把attack中的所有元素深度拷貝到temp
for(intl=0;lfor(intm=0;m//queen用來記錄皇后的位置
//那么(k,i)的位置queen[k][i]='Q'
queen[k][i]='Q';
//由于新放置了一個皇后,所以攻擊范圍又更多了
//所以需要更新attack數組
//新放置皇后的坐標為(k,i),同樣的需要更新它的八個方向
checkQueenAttack(k,i,attack);
//如果在(k,i)位置放置了皇后,那么就需要考慮在k+1行應該怎么放置其它的皇后
//遞歸的調用backtrack在k+1行放置皇后
backtrack(k+1,n,queen,attack);
//遞歸結束后,拿走皇后,恢復attack的狀態,考慮能不能在(k,i+1)的位置放置
attack=temp;
//恢復queen的狀態,說明此時皇后不放置在(k,i)位置
queen[k][i]='.';
}
}
}
//坐標(x,y)為皇后所處的位置
//更新attack
privatevoidcheckQueenAttack(intx,inty,int[][]attack){
//對于每一個坐標(x,y)來說,都有上、下、左、右、左上、左下、右上、右下八個方向
//【左上】的坐標為(x-1,y-1)
//【上】的坐標為(x-1,y)
//【右上】的坐標為(x+1,y+1)
//【左】的坐標為(x,y+1)
//【右】的坐標為(x,y-1)
//【左下】的坐標為(x+1,y-1)
//【下】的坐標為(x+1,y)
//【右下】的坐標為(x+1,y+1)
//通過兩個一維數組可以表示這八個方向
//dx表示x的方向
intdx[]={-1,-1,-1,0,0,1,1,1};
//dy表示y的方向
intdy[]={-1,0,1,-1,1,-1,0,1};
//皇后所處的坐標肯定是皇后能攻擊的位置,設置為1
attack[x][y]=1;
//以坐標(x,y)為中心,去更新它八個方向的坐標
for(intj=0;j8;j++){
//由內向外的進行更新
for(inti=1;i//新的位置的坐標行為x+i*dx[j]
intnx=x+i*dx[j];
//新的位置的坐標列為y+i*dy[j]
intny=y+i*dy[j];
//如果新位置的坐標在n*n的棋盤范圍內
if(nx>=0&&nx=0&&ny//那么這些位置就是在坐標為(x,y)的皇后的攻擊范圍內,更新為1
attack[nx][ny]=1;
}
}
}
}
}
審核編輯 :李倩
聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
-
代碼
+關注
關注
30文章
4751瀏覽量
68359 -
回溯算法
+關注
關注
0文章
10瀏覽量
6591
原文標題:回溯算法經典題目之 N 皇后
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
dp接口的最新技術發展
深度優先搜索(DFS)是一種基本的算法,用于遍歷或搜索樹或圖。它從一個頂點開始,盡可能深地搜索樹的分支。當搜索到最深節點時,然后回溯。DFS可以用于解決許多問題,如尋找路徑、檢測循環、拓撲排序等
時間復雜度為 O(n^2) 的排序算法
作者:京東保險 王奕龍 對于小規模數據,我們可以選用時間復雜度為 O(n2) 的排序算法。因為時間復雜度并不代表實際代碼的執行時間,它省去了低階、系數和常數,僅代表的增長趨勢,所以在小規模數據情況下

RVBacktrace RISC-V極簡棧回溯組件
RVBacktrace組件簡介一個極簡的RISC-V棧回溯組件。功能在需要的地方調用組件提供的唯一API,開始當前環境的棧回溯支持輸出addr2line需要的命令,使用addr2line進行棧回溯支持結合反匯編,棧

回溯英特爾在跨越半個世紀的發展歷程
我們以英特爾三位風云人物的三句名言為線索,回溯英特爾在跨越半個世紀的發展歷程中,如何利用芯片技術的力量,影響信息時代,開啟未來之門。
機器學習的經典算法與應用
關于數據機器學習就是喂入算法和數據,讓算法從數據中尋找一種相應的關系。Iris鳶尾花數據集是一個經典數據集,在統計學習和機器學習領域都經常被用作示例。數據集內包含3類共150條記錄,每類各50個數

什么是經典藍牙模塊?
? 什么是經典藍牙模塊? 前面我們已經就藍牙模塊的概念做了了解,隨著時間的推移,產品越來越智能,需要的藍牙模塊也就越來越廣泛,本篇文章我們就一起了解下什么是經典藍牙模塊。 經典藍牙模塊(BT)泛指

求助,關于STM32上開發函數調用堆棧回溯的問題求解
1、stm32f1系列
2、上了FreeRTOS
3、想開發函數調用回溯功能
在編譯選項中增加了--use_frame_pointer,編程一個正常的程序(之前一直run的),測試發現,程序啟動即crash,請問有沒有高手之前遇到過?
發表于 05-10 07:32
C語言實現經典排序算法概覽
冒泡排序(英語:Bubble Sort)是一種簡單的排序算法。它重復地走訪過要排序的數列,一次比較兩個元素,如果他們的順序(如從大到小、首字母從A到Z)錯誤就把他們交換過來。

十大排序算法總結
排序算法是最經典的算法知識。因為其實現代碼短,應該廣,在面試中經常會問到排序算法及其相關的問題。一般在面試中最常考的是快速排序和歸并排序等基本的排序
什么是后量子密碼學?量子計算機vs經典計算機
后量子密碼學(Post-Quantum Cryptography,PQC)是在經典計算機上定義和執行算法,研究量子計算機和經典計算機都無法破解的新密碼系統。后量子密碼學的提出是為了抵抗量子計算機的攻擊,所以又稱抗量子計算密碼學。
大佬總結!這篇把單片機數字濾波算法講絕了
實驗得到。
(2)中值濾波算法
該運算的過程是對某一參數連續采樣N次(N一般為奇數),然后把N次采樣的值按從小到大排列,再取中間值作為本次采樣值,整個過程實際上是一個序列排序的過程。
發表于 11-30 18:39




 回溯算法經典題目之N皇后
回溯算法經典題目之N皇后
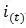










評論