用過DSP的應該都知道Q格式吧;
-
1 前言
-
2 Q數據的表示
-
2.1 范圍和精度
-
2.2 推導
-
-
3 Q數據的運算
-
3.1 0x7FFF
-
3.2 0x8000
-
3.3 加法
-
3.4 減法
-
3.5 乘法
-
3.6 除法
-
-
4 常見Q格式的數據范圍
-
5 0x5f3759df
-
6 總結
1 前言
Q格式是二進制的定點數格式,相對于浮點數,Q格式指定了相應的小數位數和整數位數,在沒有浮點運算的平臺上,可以更快地對浮點數據進行處理,以及應用在需要恒定分辨率的程序中(浮點數的精度是會變化的);
需要注意的是Q格式是概念上小數定點,通過選擇常規的二進制數整數位數和小數位數,從而達到所需要的數值范圍和精度,這里可能有點抽象,下面繼續看介紹。
2 Q數據的表示
2.1 范圍和精度
定點數通常表示為,其中m為整數個數,n為小數個數,其中最高位位符號位并且以二進制補碼的形式存儲;
- 范圍:
- 精度:
無符號的用表示;
- 范圍:
- 精度:
2.2 推導
無符號Q格式數據的推導這里以一個16位無符號整數為例,所能表示的最大數據的二進制形式如下圖所示;

所以不難看出,的范圍大小和精度;根據等比數列求和公式得到,整數域最大值如下:
小數域最大值如下:
因此的范圍滿足 ;
有符號Q格式數據的推導這里以一個16位有符號整數為例,所能表示的最大數據的二進制形式如下圖所示;

所以不難求出,的范圍大小和精度;根據等比數列求和公式得到,整數域最大值如下:
小數域最大值如下:
因此最大能表示的數為:;
所能表示的最小數據的二進制形式如下圖所示;

可以從圖中看到,該數表示為;
補充一下:負數在計算機中是補碼的形式存在的,
補碼=反碼+1,符號位為1則表示為負數;
那么-4該如何表示呢?
以8 bit數據為例,如下所示;
原碼:0B 0000 100
反碼:0B 1111 011
補碼:0B 1111 100
綜上,可以得到有符號的范圍是:
3 Q數據的運算
3.1 0x7FFF
最大數的十六進制為0x7FFF,如下圖所示;

3.2 0x8000
最小數的十六進制為0X8000,如下圖所示;

上述這兩種情況,下面都會用到。
3.3 加法
加法和減法需要兩個Q格式的數據定標相同,即和滿足以下條件;
int16_tq_add(int16_ta,int16_tb)
{
returna+b;
}
上面的程序其實并不安全,在一般的DSP芯片具有防止溢出的指令,但是通常需要做一下溢出檢測,具體如下所示;
//https://great.blog.csdn.net/
int16_tq_add_sat(int16_ta,int16_tb)
{
int16_tresult;
int32_ttmp;
tmp=(int32_t)a+(int32_t)b;
if(tmp>0x7FFF)
tmp=0x7FFF;
if(tmp-1*0x8000)
tmp=-1*0x8000;
result=(int16_t)tmp;
returnresult;
}
3.4 減法
類似于加法的操作,需要相同定標的兩個Q格式數進行相減,但是不會存在溢出的情況;
//https://great.blog.csdn.net/
int16_tq_sub(int16_ta,int16_tb)
{
returna-b;
}
3.5 乘法
乘法同樣需要考慮溢出的問題,這里通過sat16函數,對溢出做了處理;
//https://great.blog.csdn.net/
//precomputedvalue:
#defineK(1<
//saturatetorangeofint16_t
int16_tsat16(int32_tx)
{
if(x>0x7FFF)return0x7FFF;
elseif(x-0x8000)return-0x8000;
elsereturn(int16_t)x;
}
int16_tq_mul(int16_ta,int16_tb)
{
int16_tresult;
int32_ttemp;
temp=(int32_t)a*(int32_t)b;//resulttypeisoperand'stype
//Rounding;midvaluesareroundedup
temp+=K;
//Correctbydividingbybaseandsaturateresult
result=sat16(temp>>Q);
returnresult;
}
3.6 除法
//https://great.blog.csdn.net/
int16_tq_div(int16_ta,int16_tb)
{
/*pre-multiplybythebase(UpscaletoQ16sothattheresultwillbeinQ8format)*/
int32_ttemp=(int32_t)a</*Rounding:midvaluesareroundedup(downfornegativevalues).*/
/*ORcomparemostsignificantbitsi.e.if(((temp>>31)&1)==((b>>15)&1))*/
if((temp>=0&&b>=0)||(temp0&&b0)){
temp+=b/2;/*ORshift1biti.e.temp+=(b>>1);*/
}else{
temp-=b/2;/*ORshift1biti.e.temp-=(b>>1);*/
}
return(int16_t)(temp/b);
}
4 常見Q格式的數據范圍
定點數和浮點數轉換的關系滿足以下公式:
其中為,
m表示整數位數,n表示小數位數;
#include
運行得到結果如下所示;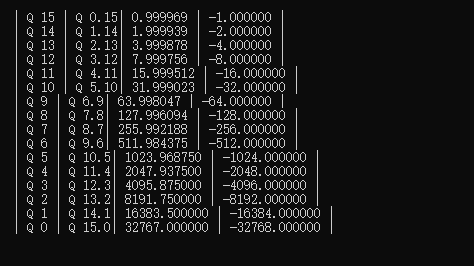
| Q | Qmn | Max | Min |
|---|---|---|---|
| Q 15 | Q 0.15 | 0.999969 | -1.000000 |
| Q 14 | Q 1.14 | 1.999939 | -2.000000 |
| Q 13 | Q 2.13 | 3.999878 | -4.000000 |
| Q 12 | Q 3.12 | 7.999756 | -8.000000 |
| Q 11 | Q 4.11 | 15.999512 | -16.000000 |
| Q 10 | Q 5.10 | 31.999023 | -32.000000 |
| Q 9 | Q 6.9 | 63.998047 | -64.000000 |
| Q 8 | Q 7.8 | 127.996094 | -128.000000 |
| Q 7 | Q 8.7 | 255.992188 | -256.000000 |
| Q 6 | Q 9.6 | 511.984375 | -512.000000 |
| Q 5 | Q 10.5 | 1023.968750 | -1024.000000 |
| Q 4 | Q 11.4 | 2047.937500 | -2048.000000 |
| Q 3 | Q 12.3 | 4095.875000 | -4096.000000 |
| Q 2 | Q 13.2 | 8191.750000 | -8192.000000 |
| Q 1 | Q 14.1 | 16383.500000 | -16384.000000 |
| Q 0 | Q 15.0 | 32767.000000 | -32768.000000 |
5 0x5f3759df
Q格式雖然十分抽象,但是且看看這個數字0x5f3759df,感覺和Q格式有某種聯系,它是雷神之錘3中的一個算法的魔數,畢竟游戲引擎需要充分考慮到效率,具體的由來可以看一下論文《Fast Inverse Square Root》,下面是源碼中剝出來的快速平方根算法;
floatQ_rsqrt(floatnumber)
{
longi;
floatx2,y;
constfloatthreehalfs=1.5F;
x2=number*0.5F;
y=number;
i=*(long*)&y;//evilfloatingpointbitlevelhacking
i=0x5f3759df-(i>>1);//whatthefuck?
y=*(float*)&i;
y=y*(threehalfs-(x2*y*y));//1stiteration
//y=y*(threehalfs-(x2*y*y));//2nditeration,thiscanberemoved
#ifndefQ3_VM
#ifdef__linux__
assert(!isnan(y));//bk010122-FPE?
#endif
#endif
returny;
}
6 總結
本文介紹了Q格式的表示方式以及相應的運算,另外需要注意在Q格式運算的時候,兩者定標必須相同,對于數據的溢出檢測也要做相應的處理。
審核編輯:湯梓紅
-
dsp
+關注
關注
552文章
7962瀏覽量
348255 -
二進制
+關注
關注
2文章
793瀏覽量
41597 -
Q格式
+關注
關注
0文章
2瀏覽量
1578
原文標題:浮點運算耗時,那試試定點運算~(C語言的Q格式)
文章出處:【微信號:嵌入式情報局,微信公眾號:嵌入式情報局】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Q格式計算
音頻信號在AIC3106和McASP之間的傳遞格式只能是Q15定點表示嗎?
F28335的Q30格式有幾位有效數字?
什么是HDV格式?什么是HDV標準?以及HDV的優點
電機的控制方式以及程序的編寫
EtherCAT 數據幀格式和尋址方式簡介





 Q格式的表示方式以及相應的運算
Q格式的表示方式以及相應的運算











評論