嵌套命名實(shí)體識(shí)別是命名實(shí)體識(shí)別中的一個(gè)頗具挑戰(zhàn)的子問(wèn)題。我們?cè)凇秾?shí)體識(shí)別LEAR論文閱讀筆記》與《實(shí)體識(shí)別BERT-MRC論文閱讀筆記》中已經(jīng)介紹過(guò)針對(duì)這個(gè)問(wèn)題的兩種方法。今天讓我們通過(guò)本文來(lái)看看在嵌套實(shí)體識(shí)別上哪一個(gè)方法更勝一籌。

1. 嵌套實(shí)體識(shí)別

1.1 什么是嵌套實(shí)體識(shí)別

嵌套實(shí)體識(shí)別是命名實(shí)體識(shí)別中一個(gè)子問(wèn)題。那么什么才是嵌套實(shí)體呢？我們看下面這個(gè)例子：

“北京天安門”是地點(diǎn)實(shí)體；

“北京天安門”中“北京”也是地點(diǎn)實(shí)體；兩者存在嵌套關(guān)系。

1.2 嵌套實(shí)體識(shí)別方法

CRF等傳統(tǒng)序列標(biāo)注方法無(wú)法應(yīng)用于嵌套實(shí)體識(shí)別。現(xiàn)階段，業(yè)界比較流行的是構(gòu)建實(shí)體矩陣，即用一個(gè)矩陣 來(lái)代表語(yǔ)料中的所有實(shí)體及其類型。

其中任一元素 表示類為 ，起點(diǎn)為 ，結(jié)尾為 的實(shí)體。比如在下圖所示實(shí)體矩陣中，就有兩個(gè)Location類的實(shí)體：北京、北京天安門。

通過(guò)這樣的標(biāo)注方式我們可以對(duì)任何嵌套實(shí)體進(jìn)行標(biāo)注，從而解決訓(xùn)練和解碼的問(wèn)題。

在本文中，我們將對(duì)比目前接觸到的部分實(shí)體矩陣的構(gòu)建方法在 CMeEE 數(shù)據(jù)集（醫(yī)學(xué)NER，有一定比例的嵌套實(shí)體）上的表現(xiàn)。

2. 實(shí)體矩陣構(gòu)建框架

2.1 變量與符號(hào)約定

為了方便后續(xù)對(duì)比說(shuō)明，這里我們先定義幾個(gè)統(tǒng)一的變量與符號(hào)。

首先，上文中 表示類為 ，起點(diǎn)為 ，結(jié)尾為 的實(shí)體。

在本實(shí)驗(yàn)中，我們均使用 bert-base-chinese 作為 編碼器。假設(shè) 表示最后一層隱藏層中第 個(gè) token 的 embedding，那么 和 分別表示經(jīng)過(guò)編碼器之后實(shí)體 start 和 end token 的embedding。

我們有公式 ，其中 就表示我們所需要對(duì)比的實(shí)體矩陣構(gòu)建頭（姑且這么稱呼）。

2.2 相關(guān)配置

在對(duì)比實(shí)驗(yàn)中，除了不同實(shí)體矩陣構(gòu)建頭對(duì)應(yīng)的batch_size，learning_rate不同，所使用的編碼器、損失函數(shù)、評(píng)估方式以及訓(xùn)練輪次均保持一致。

2.3 對(duì)比方法

本文選取了四種實(shí)體矩陣構(gòu)建方法進(jìn)行比較，分別是：

GlobalPointer；

TPLinker（Muti-head selection)；

Tencent Muti-head；

Deep Biaffine（雙仿射）。

3. 代碼實(shí)現(xiàn)

3.1 GlobalPointer

GlobalPointer 出自蘇劍林的博客GlobalPointer：用統(tǒng)一的方式處理嵌套和非嵌套NER[1]。

Global Pointer 的核心計(jì)算公式為：

其中 ，。

GlobalPointer 的核心思想類似 attention的打分機(jī)制，將多個(gè)實(shí)體類型的識(shí)別視為 Muti-head機(jī)制，將每一個(gè)head視為一種實(shí)體類型識(shí)別任務(wù)，最后利用attention的score(QK)作為最后的打分。

為考慮Start和end之間距離的關(guān)鍵信息，作者在此基礎(chǔ)上引入了旋轉(zhuǎn)式位置編碼（RoPE），在其文中顯示引入位置信息能給結(jié)果帶來(lái)極大提升，符合預(yù)期先驗(yàn)。

classGlobalPointer(Module):
"""全局指針模塊
將序列的每個(gè)(start,end)作為整體來(lái)進(jìn)行判斷
"""
def__init__(self,heads,head_size,hidden_size,RoPE=True):
super(GlobalPointer,self).__init__()
self.heads=heads
self.head_size=head_size
self.RoPE=RoPE
self.dense=nn.Linear(hidden_size,self.head_size*self.heads*2)

defforward(self,inputs,mask=None):
inputs=self.dense(inputs)
inputs=torch.split(inputs,self.head_size*2,dim=-1)
inputs=torch.stack(inputs,dim=-2)
qw,kw=inputs[...,:self.head_size],inputs[...,self.head_size:]
#RoPE編碼
ifself.RoPE:
pos=SinusoidalPositionEmbedding(self.head_size,'zero')(inputs)
cos_pos=pos[...,None,1::2].repeat(1,1,1,2)
sin_pos=pos[...,None,::2].repeat(1,1,1,2)
qw2=torch.stack([-qw[...,1::2],qw[...,::2]],4)
qw2=torch.reshape(qw2,qw.shape)
qw=qw*cos_pos+qw2*sin_pos
kw2=torch.stack([-kw[...,1::2],kw[...,::2]],4)
kw2=torch.reshape(kw2,kw.shape)
kw=kw*cos_pos+kw2*sin_pos
#計(jì)算內(nèi)積
logits=torch.einsum('bmhd,bnhd->bhmn',qw,kw)
#排除padding,排除下三角
logits=add_mask_tril(logits,mask)
returnlogits/self.head_size**0.5

3.2 TPLinker

TPLinker 來(lái)自論文《TPLinker: Single-stage Joint Extraction of Entities and Relations Through Token Pair Linking》[2]。

TPLinker 原本是為解決實(shí)體關(guān)系抽取設(shè)計(jì)的方法，原型為《Joint entity recognition and relation extraction as a multi-head selection problem》[3]論文中的 Muti-head selection機(jī)制。此處選取其中用于識(shí)別實(shí)體部分的機(jī)制，作為對(duì)比方法。

TPLinker中相應(yīng)的計(jì)算公式如下：

，

其中

與GlobalPointer不同的是，GlobalPointer 是乘性的，而 Muti-head是加性的。這兩種機(jī)制，誰(shuí)的效果更好，我們無(wú)法僅通過(guò)理論進(jìn)行分析，因此需要做相應(yīng)的對(duì)比實(shí)驗(yàn)，從結(jié)果進(jìn)行倒推。但是在實(shí)際實(shí)現(xiàn)的過(guò)程中，筆者發(fā)現(xiàn)加性比乘性占用更多的內(nèi)存，但是與GlobalPointer中不同的是，加性仍然能實(shí)現(xiàn)快速并行，需要在計(jì)算設(shè)計(jì)上加入一些技巧。

classMutiHeadSelection(Module):

def__init__(self,hidden_size,c_size,abPosition=False,rePosition=False,maxlen=None,max_relative=None):
super(MutiHeadSelection,self).__init__()
self.hidden_size=hidden_size
self.c_size=c_size
self.abPosition=abPosition
self.rePosition=rePosition
self.Wh=nn.Linear(hidden_size*2,self.hidden_size)
self.Wo=nn.Linear(self.hidden_size,self.c_size)
ifself.rePosition:
self.relative_positions_encoding=relative_position_encoding(max_length=maxlen,
depth=2*hidden_size,max_relative_position=max_relative)

defforward(self,inputs,mask=None):
input_length=inputs.shape[1]
batch_size=inputs.shape[0]
ifself.abPosition:
#由于為加性拼接，我們無(wú)法使用RoPE,因此這里直接使用絕對(duì)位置編碼
inputs=SinusoidalPositionEmbedding(self.hidden_size,'add')(inputs)
x1=torch.unsqueeze(inputs,1)
x2=torch.unsqueeze(inputs,2)
x1=x1.repeat(1,input_length,1,1)
x2=x2.repeat(1,1,input_length,1)
concat_x=torch.cat([x2,x1],dim=-1)
#與TPLinker原論文中不同的是，通過(guò)重復(fù)+拼接的方法構(gòu)建的矩陣能滿足并行計(jì)算的要求。
ifself.rePosition:
#如果使用相對(duì)位置編碼，我們則直接在矩陣上實(shí)現(xiàn)相加
relations_keys=self.relative_positions_encoding[:input_length,:input_length,:].to(inputs.device)
concat_x+=relations_keys
hij=torch.tanh(self.Wh(concat_x))
logits=self.Wo(hij)
logits=logits.permute(0,3,1,2)
logits=add_mask_tril(logits,mask)
returnlogits

3.3 Tencent Muti-head

《EMPIRICAL ANALYSIS OF UNLABELED ENTITY PROBLEM IN NAMED ENTITY RECOGNITION》[4] 提出了一種基于片段標(biāo)注解決實(shí)體數(shù)據(jù)標(biāo)注缺失的訓(xùn)練方法，并在部分?jǐn)?shù)據(jù)集上達(dá)到了SOTA。關(guān)注其實(shí)體矩陣構(gòu)建模塊，相當(dāng)于Muti-head的升級(jí)版，因此我把它叫做Tencent Muti-head。

Tencent Muti-head的計(jì)算公式如下：

其中

與TPLinker相比，Tencent Muti-head在加性的基礎(chǔ)上加入了更多信息交互元素，比如 （作差與點(diǎn)乘），但同時(shí)也提高了內(nèi)存的占用量。

classTxMutihead(Module):

def__init__(self,hidden_size,c_size,abPosition=False,rePosition=False,maxlen=None,max_relative=None):
super(TxMutihead,self).__init__()
self.hidden_size=hidden_size
self.c_size=c_size
self.abPosition=abPosition
self.rePosition=rePosition
self.Wh=nn.Linear(hidden_size*4,self.hidden_size)
self.Wo=nn.Linear(self.hidden_size,self.c_size)
ifself.rePosition:
self.relative_positions_encoding=relative_position_encoding(max_length=maxlen,
depth=4*hidden_size,max_relative_position=max_relative)

defforward(self,inputs,mask=None):
input_length=inputs.shape[1]
batch_size=inputs.shape[0]
ifself.abPosition:
#由于為加性拼接，我們無(wú)法使用RoPE,因此這里直接使用絕對(duì)位置編碼
inputs=SinusoidalPositionEmbedding(self.hidden_size,'add')(inputs)
x1=torch.unsqueeze(inputs,1)
x2=torch.unsqueeze(inputs,2)
x1=x1.repeat(1,input_length,1,1)
x2=x2.repeat(1,1,input_length,1)
concat_x=torch.cat([x2,x1,x2-x1,x2.mul(x1)],dim=-1)
ifself.rePosition:
relations_keys=self.relative_positions_encoding[:input_length,:input_length,:].to(inputs.device)
concat_x+=relations_keys
hij=torch.tanh(self.Wh(concat_x))
logits=self.Wo(hij)
logits=logits.permute(0,3,1,2)
logits=add_mask_tril(logits,mask)
returnlogits

3.4 Deep Biaffine

此處使用的雙仿射結(jié)構(gòu)出自《Named Entity Recognition as Dependency Parsing》[5]。原文用于識(shí)別實(shí)體依存關(guān)系，因此也可以直接用于實(shí)體命名識(shí)別。

Deep Biaffine的計(jì)算公式如下：

簡(jiǎn)單來(lái)說(shuō)雙仿射分別 為頭 為尾的實(shí)體類別后驗(yàn)概率建模 + 對(duì) 或 為尾的實(shí)體類別的后驗(yàn)概率分別建模 + 對(duì)實(shí)體類別 的先驗(yàn)概率建模。

不難看出Deep Biaffine是加性與乘性的結(jié)合。在筆者復(fù)現(xiàn)的關(guān)系抽取任務(wù)中，雙仿射確實(shí)帶來(lái)的一定提升，但這種建模思路在實(shí)體識(shí)別中是否有效還有待驗(yàn)證。

classBiaffine(Module):

def__init__(self,in_size,out_size,Position=False):
super(Biaffine,self).__init__()
self.out_size=out_size
self.weight1=Parameter(torch.Tensor(in_size,out_size,in_size))
self.weight2=Parameter(torch.Tensor(2*in_size+1,out_size))
self.Position=Position
self.reset_parameters()

defreset_parameters(self):
torch.nn.init.kaiming_uniform_(self.weight1,a=math.sqrt(5))
torch.nn.init.kaiming_uniform_(self.weight2,a=math.sqrt(5))

defforward(self,inputs,mask=None):
input_length=inputs.shape[1]
hidden_size=inputs.shape[-1]
ifself.Position:
#引入絕對(duì)位置編碼，在矩陣乘法時(shí)可以轉(zhuǎn)化為相對(duì)位置信息
inputs=SinusoidalPositionEmbedding(hidden_size,'add')(inputs)
x1=torch.unsqueeze(inputs,1)
x2=torch.unsqueeze(inputs,2)
x1=x1.repeat(1,input_length,1,1)
x2=x2.repeat(1,1,input_length,1)
concat_x=torch.cat([x2,x1],dim=-1)
concat_x=torch.cat([concat_x,torch.ones_like(concat_x[...,:1])],dim=-1)
#bxi,oij,byj->boxy
logits_1=torch.einsum('bxi,ioj,byj->bxyo',inputs,self.weight1,inputs)
logits_2=torch.einsum('bijy,yo->bijo',concat_x,self.weight2)
logits=logits_1+logits_2
logits=logits.permute(0,3,1,2)
logits=add_mask_tril(logits,mask)
returnlogits

4. 實(shí)驗(yàn)結(jié)果

實(shí)驗(yàn)所用的GPU為: P40 24G (x1)。為了把各方法的內(nèi)存占用情況考慮在內(nèi)，本次對(duì)比實(shí)驗(yàn)全都在一張P40 24G的GPU上進(jìn)行，并把Batch_size開(kāi)到最大：

僅GlobalPointer可達(dá)到16；

Tencent Muti-head batch_size只能達(dá)到4。

Tencent Muti-head因?yàn)樾枰獦?gòu)建超大矩陣，所以占用內(nèi)存較大，batch_size最大只能到4。從中，我們可以看出GlobalPointer的性能優(yōu)勢(shì)。

需要注意的是，我們這里只比較了各方法在訓(xùn)練過(guò)程中在驗(yàn)證集上的最好表現(xiàn)：

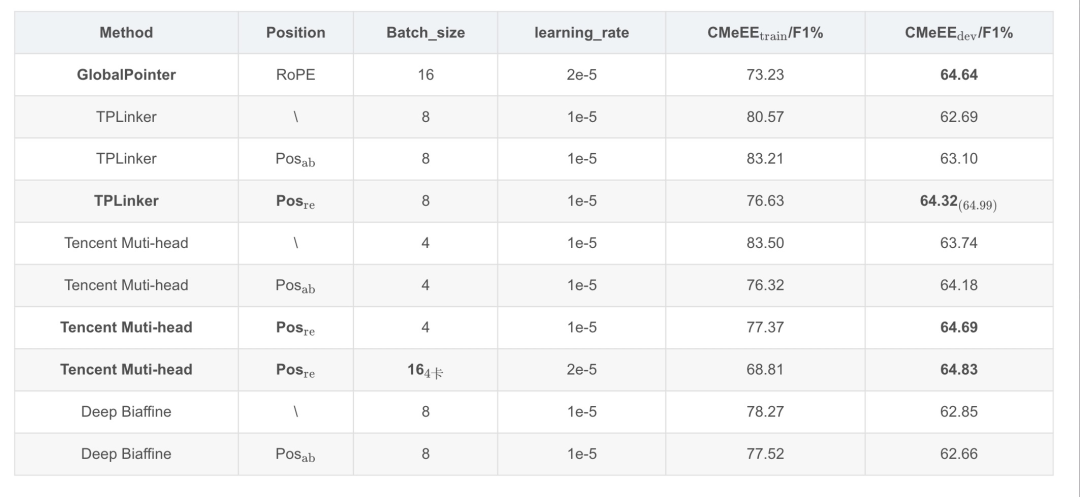
總結(jié)

GlobalPointer作為乘性方法，在空間內(nèi)存占用上明顯優(yōu)于其他方法，并且訓(xùn)練速度較快，能達(dá)到一個(gè)具有競(jìng)爭(zhēng)力的效果。

TPLinker 和 Tencent Muti-head作為加性方法，在優(yōu)化過(guò)程中均表現(xiàn)出 相對(duì)位置編碼 > 絕對(duì)位置編碼 > 不加入位置編碼 的特征。這意味著在通過(guò)構(gòu)建實(shí)體矩陣進(jìn)行實(shí)體命名識(shí)別時(shí)位置信息具有絕對(duì)重要的優(yōu)勢(shì)，且直接引入相對(duì)位置信息較優(yōu)。

在絕對(duì)位置編碼和不加入位置編碼的測(cè)試中Tencent Muti-head的效果明顯優(yōu)于TPLinker而兩者均差于GlobalPointer，但在引入相對(duì)位置信息后Tencent Muti-head略微超越了GlobalPointer，而TPLinker提點(diǎn)顯著，作為Tencent Muti-head的原型在最高得分上甚至可能有更好的表現(xiàn)。

Biaffine雙仿射表現(xiàn)不佳，意味著這種建模思路不適合用于實(shí)體命名識(shí)別。

在計(jì)算資源有限的情況下GlobalPointer是最優(yōu)的baseline選擇，如果擁有足夠的計(jì)算資源且對(duì)訓(xùn)練、推理時(shí)間的要求較為寬松，嘗試使用TPLinker/Tencent Muti-head + 相對(duì)位置編碼或許能取得更好的效果。