本節將詳細講解切比雪夫濾波器(ChebyshevI和ChebyshevII)的綜合設計,結合之前電路仿真的工作,現將Chebyshev型濾波器集成到了濾波器設計App中,提供一個試用版本,并提供GitHub開源鏈接。
切比雪夫濾波器特點和用途
Chebyshev(切比雪夫)濾波器是Cauer于1930-1931年首先使用切比雪夫多項式(Chebyshev polynomials)逼近來進行設計的濾波器,其特點是通帶內具有等紋波特性,對比Butterworth濾波器其更具陡峭的截止特性,被廣泛用于實際工程應用之中。
另外,實際上Butterworth濾波器是Chebyshev濾波器在紋波為0的一個特殊情況(文中有解釋)。
關于Chebyshev(Pafnuty Lvovich Chebyshev ,俄語原名: Пафну?тий Льво?вич Чебышёв, IPA: [p?f?nut??j ?l?vov??t? t??b???of], 英語曾用名: Tchebycheff, 法語:Tchebyshev,德語:Tschebyschow,中文名:切比雪夫,車比雪夫)本人的相關信息可以參考陳關榮|切比雪夫,他帶起了俄羅斯現代數學的發展。
切比雪夫多項式(Chebyshev polynomials)
首先我們要清楚Cauer當年怎么想到使用切比雪夫多項式來進行濾波器設計的,這里我們要明白一個概念--濾波器逼近(Filter Approximation)。通過電路分析章節可知,我們可以通過電路實現一個多項式,那么反過來,我們可以由一個多項式實現一個電路,為了實現一個特定頻率響應的濾波器,問題轉換為找到一個合適的多項式來對濾波器進行逼近。
以頻率響應曲線為目標的濾波器設計最關鍵的是對0附近進行擬合,是不是有點懵,對吧,0有什么好擬合的,不就好了嘛,對于濾波器而言,我們希望在無窮頻率遠處衰減為無窮(也可以從能量角度來理解,頻率無限遠處能量必須為0),要求當的時候,所以必須是一個以x為自變量的多項式。
最簡單的我們可以用:來擬合,讓我們看看效果:
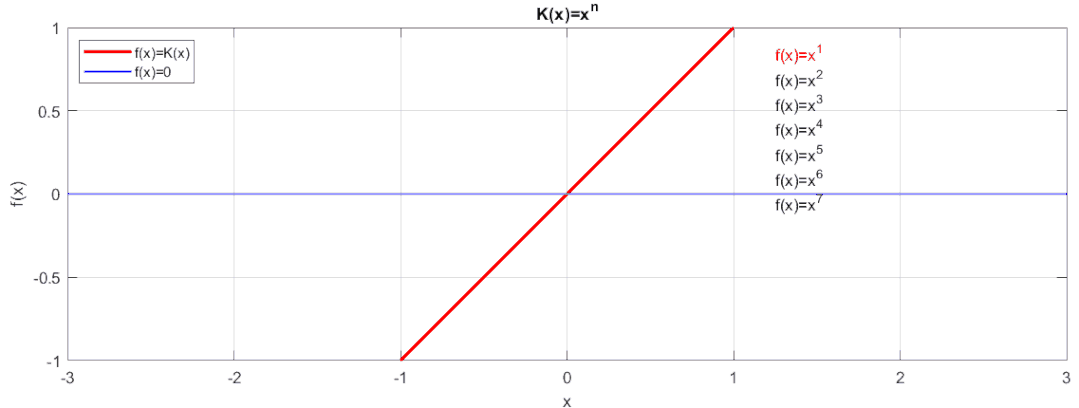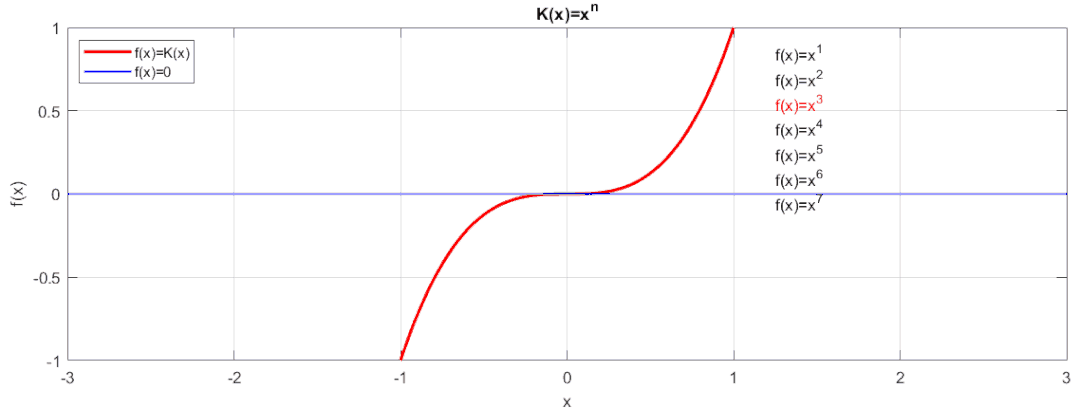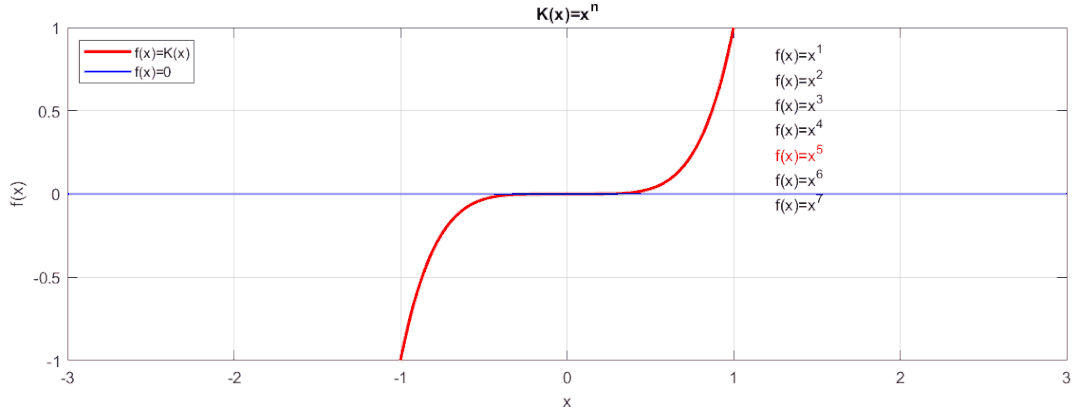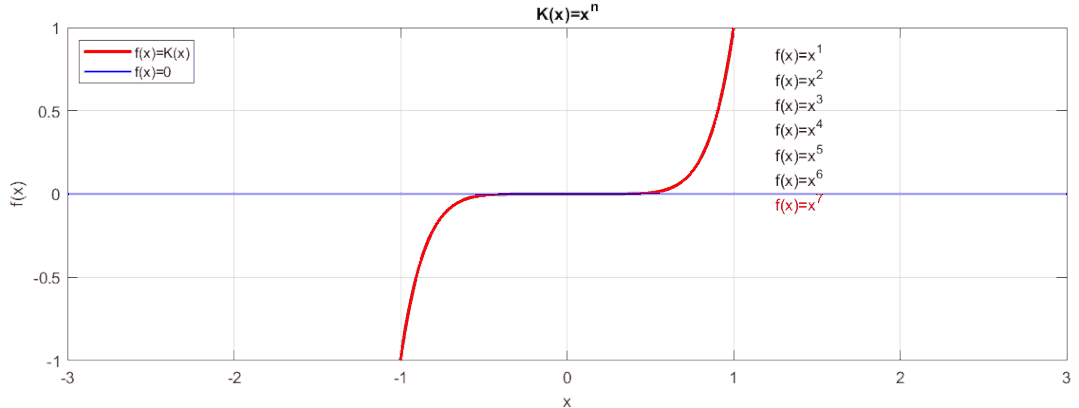
相信大家也看到了,這種擬合是不是隨著n的增大,函數值在[-1,1]范圍內越接近于0。
我們還有更好的多項式(或函數)來逼近0嗎?
有!那就是切比雪夫多項式(字母T就是切比雪夫音譯的首字母):大家看到沒有,函數值被限制在cos函數的正負1以內,這也是等紋波的底層原因。
做億點點變形,看看切比雪夫多項式原本的模樣:
當時:
當時:
當時,使用三角函數的倍角公式得到:令即可得到切比雪夫多項式的遞推公式(可用歸納法證明):由遞推公式可以得到不同值下的切比雪夫多項式,來看看實際的函數值和0值得逼近效果:
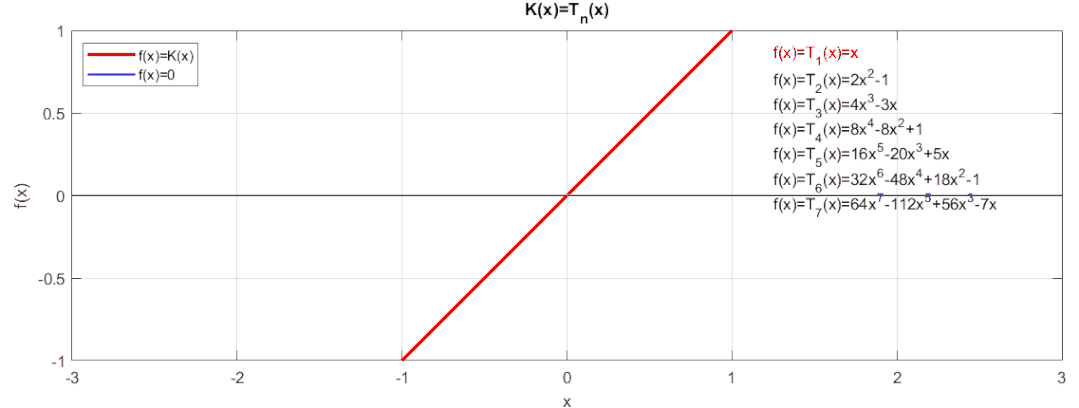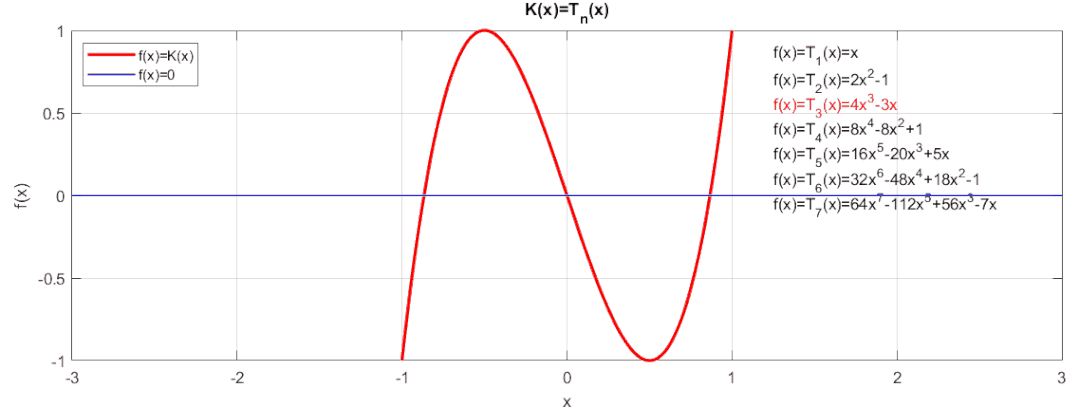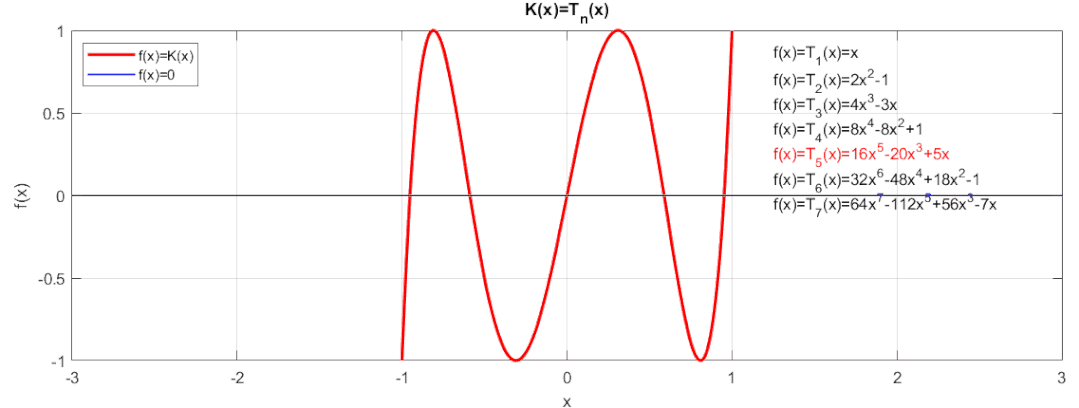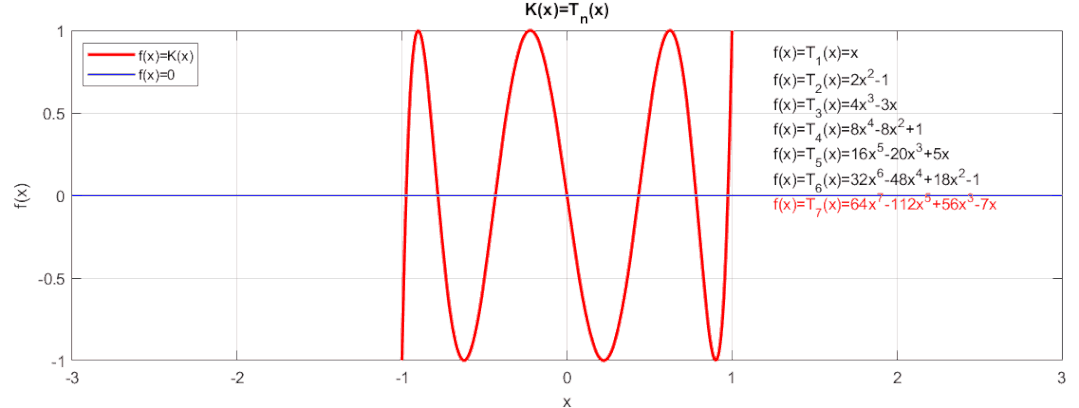
這等紋波的逼近效果是不是非常棒呢,在[-1,1]區間內,誤差絕對不會超過+/-1。
這里的簡單多項式和切比雪夫多項式實際上就是濾波器的特征多項式(另,特征函數的嚴格定義是)。當時,就是Butterworth濾波器的特征多項式,當時,就是切比雪夫濾波器的特征多項式。
寫到這里實際上本合集最初的目標基本要實現了--綜合得到直線衰減特性的濾波器。我們只需要綜合出逼近的特征多項式就可以完成濾波器的綜合,這里暫時不展開,先挖個坑,后面續繼續聊。
匹配型切比雪夫低通濾波器的綜合
匹配型濾波器表示輸入輸出阻抗不為0且相等,這時濾波器兩端都與終端阻抗相互匹配,濾波器負載電阻可以獲得信號源最大功率。
匹配型奇數階切比雪夫低通濾波器的頻率傳遞函數為:其中是濾波器紋波大小(由于在通帶范圍內是,所以我們可以控制就可控制紋波大小),是切比雪夫多項式.
得到傳遞函數后首先通過解析開拓計算出極點,選擇左半邊極點可以獲得,由特征函數解析開拓,選擇合適的零點得到,然后由和得到歸一化阻抗,最后通過輾轉相除得到元器件值。
我們以3階切比雪夫濾波器為例說明綜合過程,紋波,帶寬為,源阻抗為,負載阻抗為:
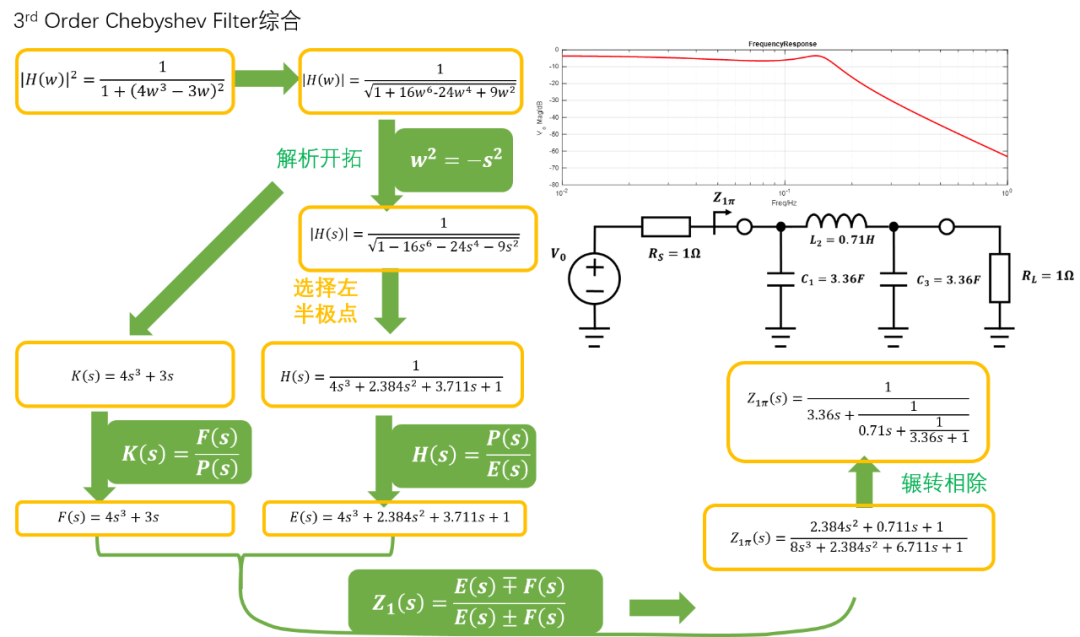
匹配型切比雪夫濾波器有現成的參數計算公式:詳細推導過程可以參考。
匹配型偶數階切比雪夫低通濾波器傳遞函數假設還用前式,不知道有沒有發現一個問題,當時:所以對于偶數階切比雪夫濾波器,則得到:由于切比雪夫濾波器紋波不為0,所以有,這和匹配型的最初定義相互矛盾,所以在匹配狀態下我們不能使用和奇數階濾波器相同的傳遞函數表達式。
那么如何解決這一問題的呢?
使用頻率變換的方法,對于一個4階的低通濾波器,我們可以這樣轉化達到目的:
將4階低通濾波器的形狀轉化為一個3階低通濾波器的形狀,我們找到4階低通濾波器的最接近0頻率的且衰減為0的一個點,我們想要的是當輸入頻率時,給到函數的頻率,當輸入頻率為時,給到函數的頻率,當輸入頻率為無窮是,給到函數的頻率也為無窮,相當于將4次濾波器的往0頻壓縮,如下動圖所示效果(藍色線為原始切比雪夫函數的4階濾波器,紅色線顯示了通過頻率變換后的4階頻率響應曲線,頻率變換后,其截止特性要比原本的差一點,但是總的來說比低一階的要好):
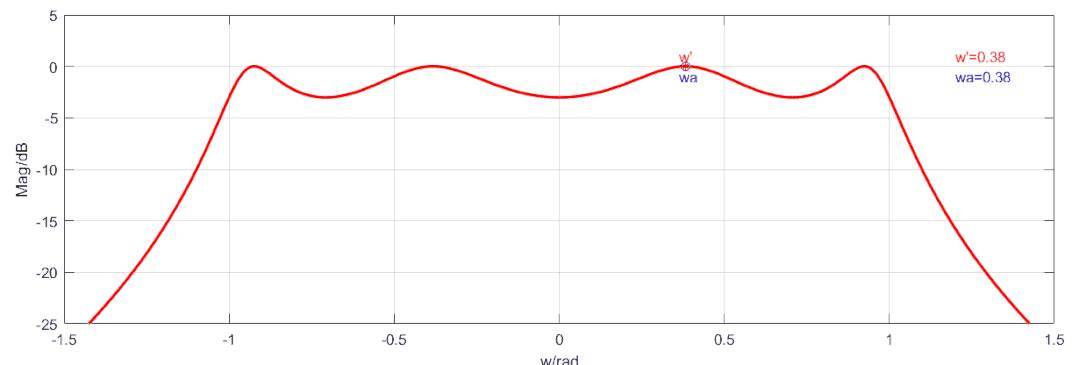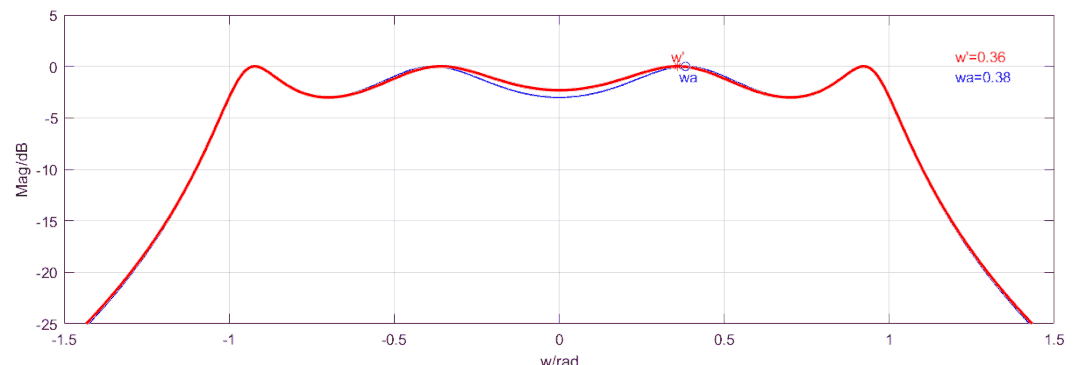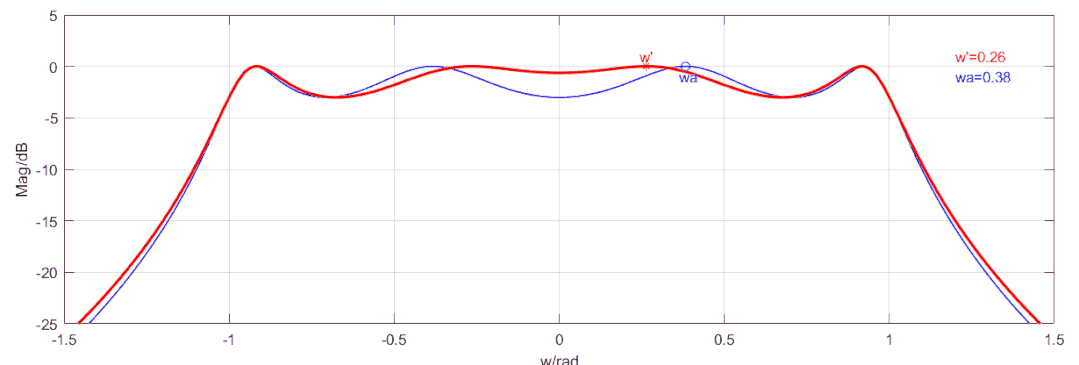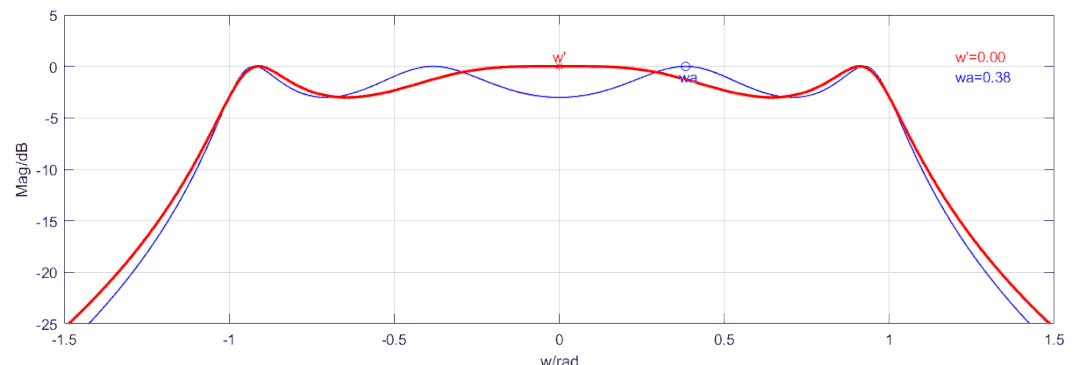
頻率變換公式如下:其中,可以滿足上述要求,所以最終得到偶數階匹配的切比雪夫低通濾波器傳遞函數為:下圖為4階切比雪夫低通濾波器的設計過程,紋波,帶寬為,源阻抗為,負載阻抗為:
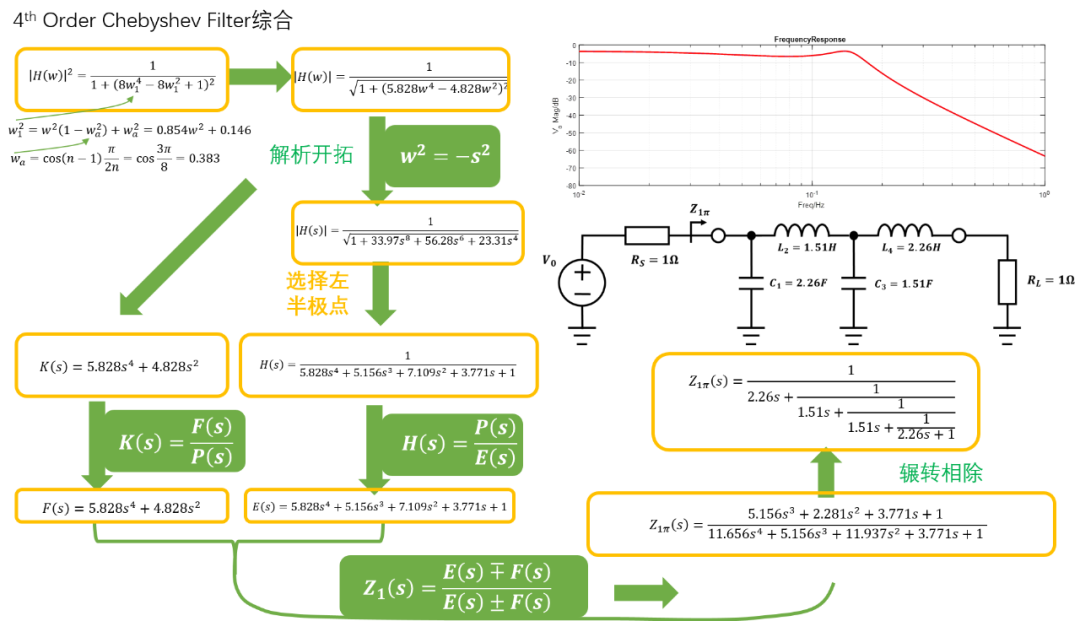
偶數階切比雪夫濾波器綜合沒有現成的公式,只能使用這種輾轉相除的辦法去綜合實際器件,為了普適性,濾波器軟件中采用輾轉相除法計算器件系數。
由衰減確定濾波器階數
設濾波器綜合中通帶頻率為,其紋波為dB,截止頻率為,衰減為dB.示意圖如下:
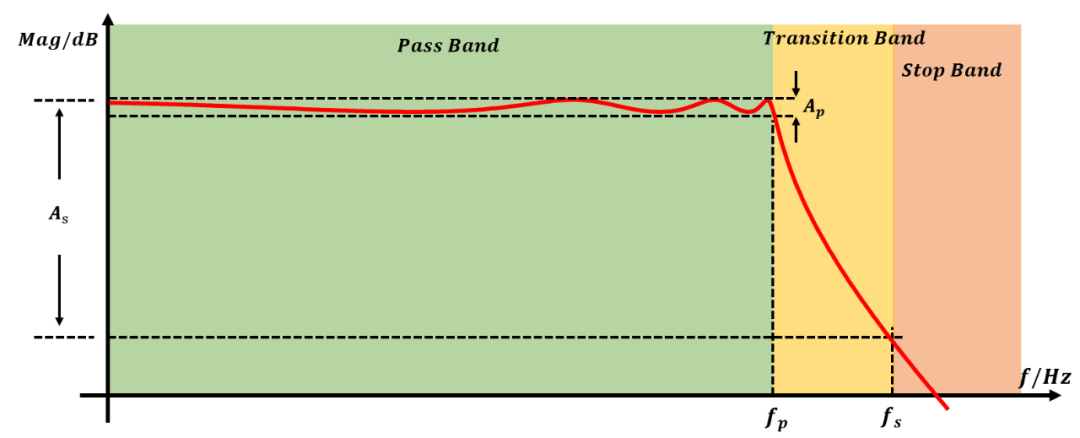
所要求的通帶到阻帶的衰減是,可以通過計算得到衰減和階數關系為:當比較大時相同條件下切比雪夫濾波器的衰減比巴特沃斯濾波器衰減大.
非匹配型切比雪夫濾波器綜合
非匹配型切比雪夫濾波器的頻率傳遞函數為:其中是一個"增益因子",這個增益因子的求解可以通過在時求解,當時,濾波器為直通狀態,整個電路就是兩個電阻的分壓,計算有效衰減值得到:如則得到。
這里要注意的是濾波器設計中的傳遞函數計算使用的是有效衰減值,而不是插入損耗,兩者有明顯的區別。有效衰減計算的是負載所獲得的功率比上負載可能獲得的最大功率;而插入損耗是系統中接入網絡后的輸出電壓比不接入網絡輸出電壓比。
有效衰減定義:插入衰減定義兩者關系,如下:當時,兩者衰減量一致,但是當時,這兩者存在明顯差異,總是要大于,這種差異在衰減器設計中尤其會誤導設計人員,如, ,這時若使用不同的衰減來計算會得到不同的結果,大多數情況下設計軟件采用的是有效衰減,但是有效衰減有個致命缺陷是當或時,定義會失效,其根本原因是有效衰減是以功率計算的,當滿足上述條件時,負載獲得的功率為0,這會使得定義失去意義。
非匹配型切比雪夫濾波器的極點位置和匹配性的完全相同,唯一不同的是特征函數。
使用解析開拓來進行求解,其他過程相同,具體推導過程見附件資料。
切比雪夫濾波器的零極點分析
切比雪夫低通濾波器的極點在一個橢圓上,可以通過的公式(這里僅僅討論匹配型切比雪夫濾波器)進行推導:令公式的分母等于0,得到極點位置公式為:根據切比雪夫公式得到:還是使用歐拉公式:通過求解得到:
實部:虛部:其中:可見的極點落在一個橢圓上,我們取復平面的左邊極點即可得到的通項公式。
不同通帶類型濾波器零極點圖如下:
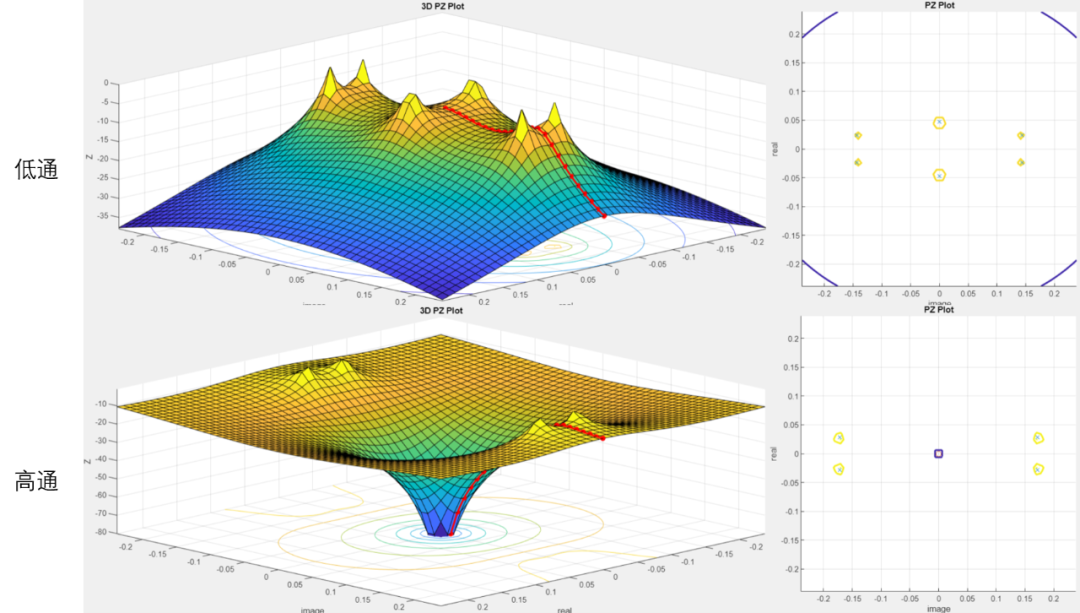
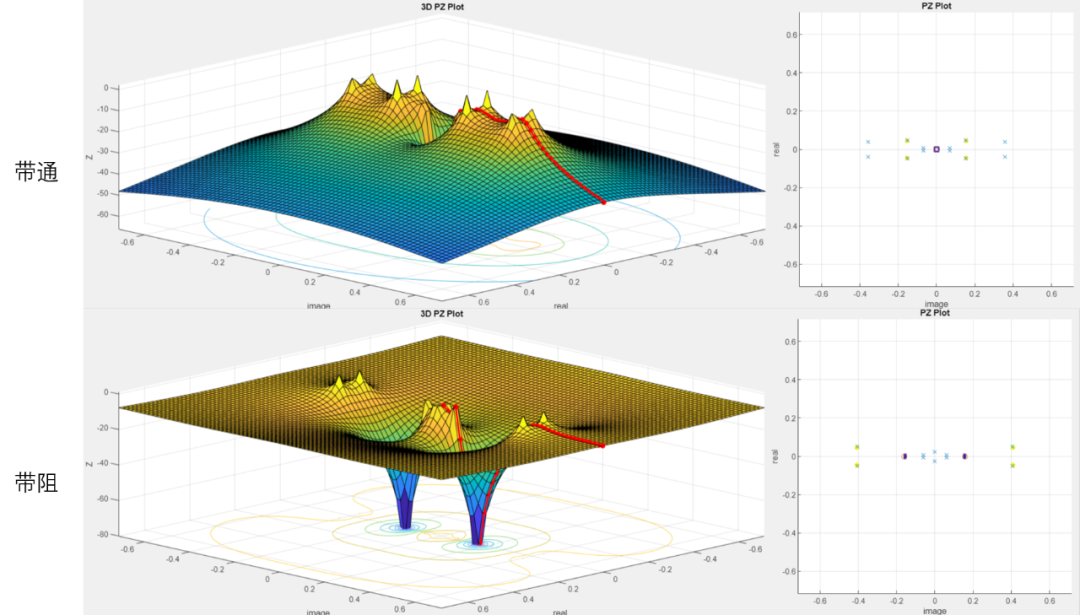
設低通極點位置為則:
高通極點位置為:帶通極點位置為(表示):
帶阻極點位置為(表示):
不同濾波器通帶類型之間的轉換
只要有了低通原型,其他濾波器通帶類型之間的轉換同模擬無源濾波器設計(五)-Butterworth濾波器設計詳解。
逆切比雪夫濾波器設計
逆切比雪夫(Inverse Chebyshev)濾波器也稱為Chebyshev II濾波器,其特點是有最平坦的通帶頻率響應,阻帶具有等紋波特性。那么怎么從切比雪夫濾波器出發推導出切比雪夫濾波器呢?
請看如下變換關系:
首先考慮切比雪夫低通濾波器在通帶內具有等紋波特性,阻帶隨著頻率升高幅度逐漸衰減到0,同之前分析高通濾波器那樣,使用替代即可得到高通濾波器特性,從圖形中可以看到,若我們用1減去這個高通濾波器,則可以得到逆切比雪夫濾波器,如下動畫展示了此過程:
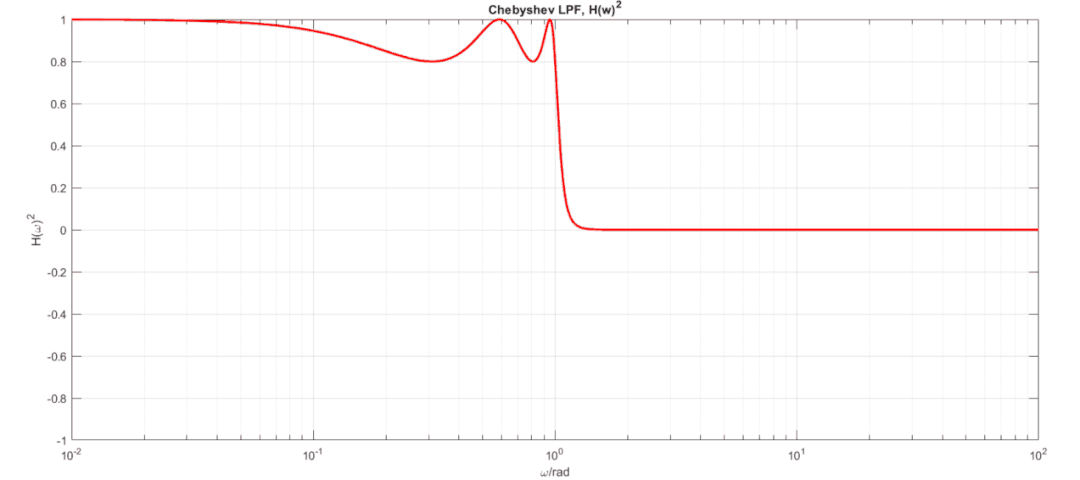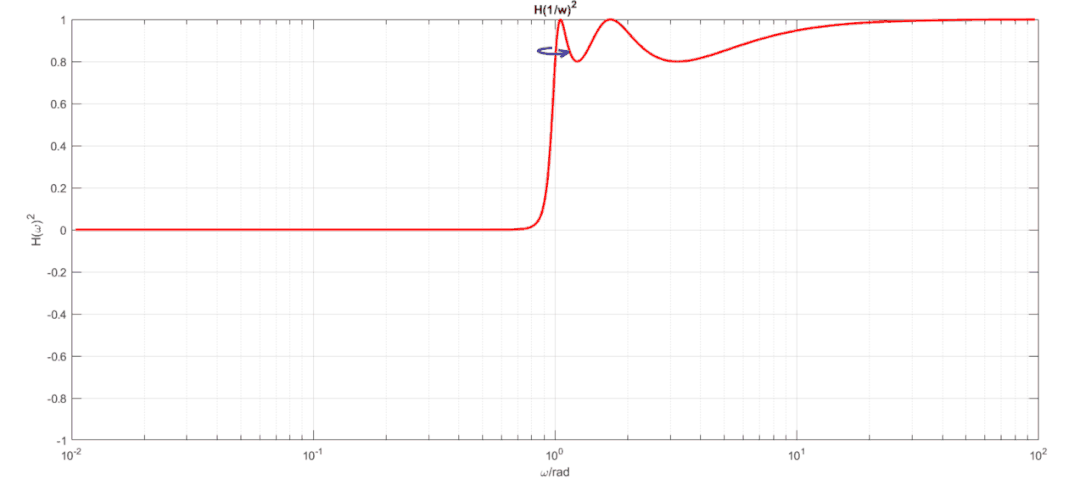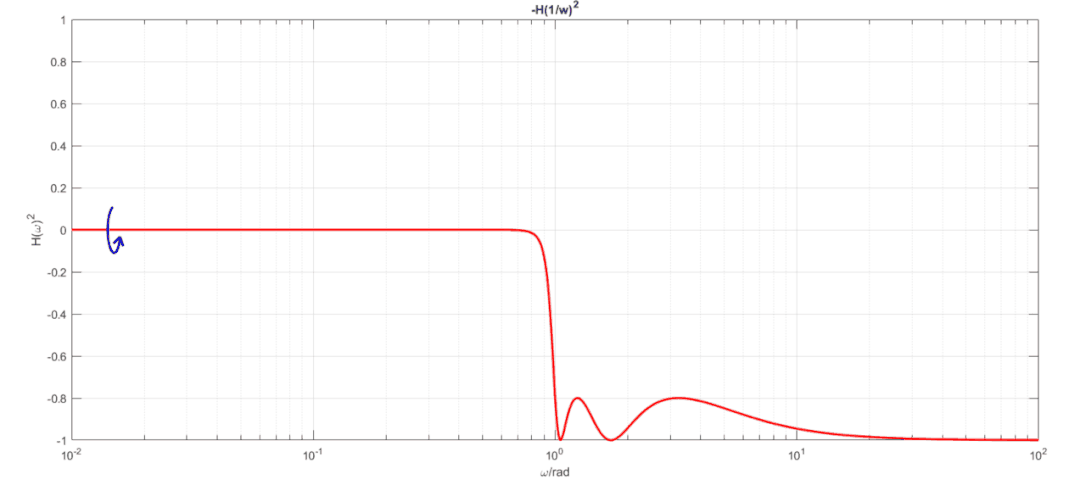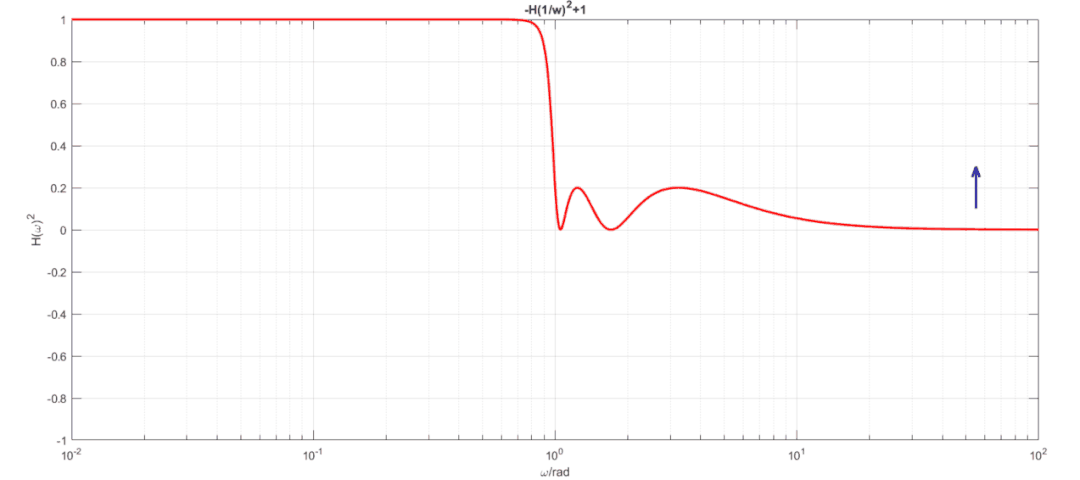
通過這個變換我們得到了逆切比雪夫濾波器幅度公式:從中可以看到逆切比雪夫濾波器除了有極點還有零點。
逆切比雪夫濾波器零點位置為:極點位置為:逆切比雪夫濾波器的極點和切比雪夫濾波器極點互為倒數。
在進行逆切比雪夫濾波器設計時也需要特別注意偶數階濾波器設計,也是需要和前述切比雪夫濾波器一樣進行頻率變換的。原因可以這樣理解,由于未變換前逆切比雪夫濾波器在頻率為無窮大時不可能衰減不為0,所以需要進行頻率變換讓頻率無窮大時濾波器衰減為0.
逆切比雪夫濾波器是從切比雪夫濾波器導出,原切比雪夫濾波器的3dB截止頻率點變為逆切比雪夫的截止頻率點,所以截止頻率位置也需要進行頻率變換:逆切比雪夫濾波器的器件綜合過程中,由于存在零點,故再也不能使用全極點的輾轉相除的辦法求得器件參數值,只能通過零點移位技術(Zero-Shifting Technique)來求得器件參數,Matlab代碼中已經實現了這一過程。
如下圖所示為匹配型3階逆切比雪夫濾波器的綜合過程,衰減,紋波,帶寬為,源阻抗為,負載阻抗為:
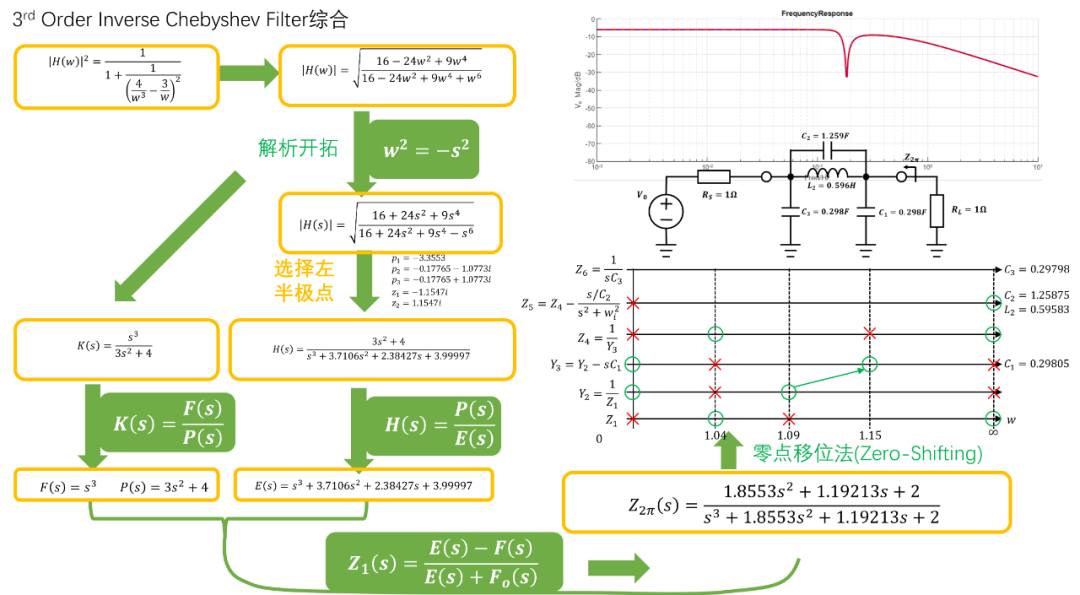
如下圖所示為非匹配性3階逆切比雪夫濾波器的綜合過程,衰減,紋波,帶寬為,源阻抗為,負載阻抗為:
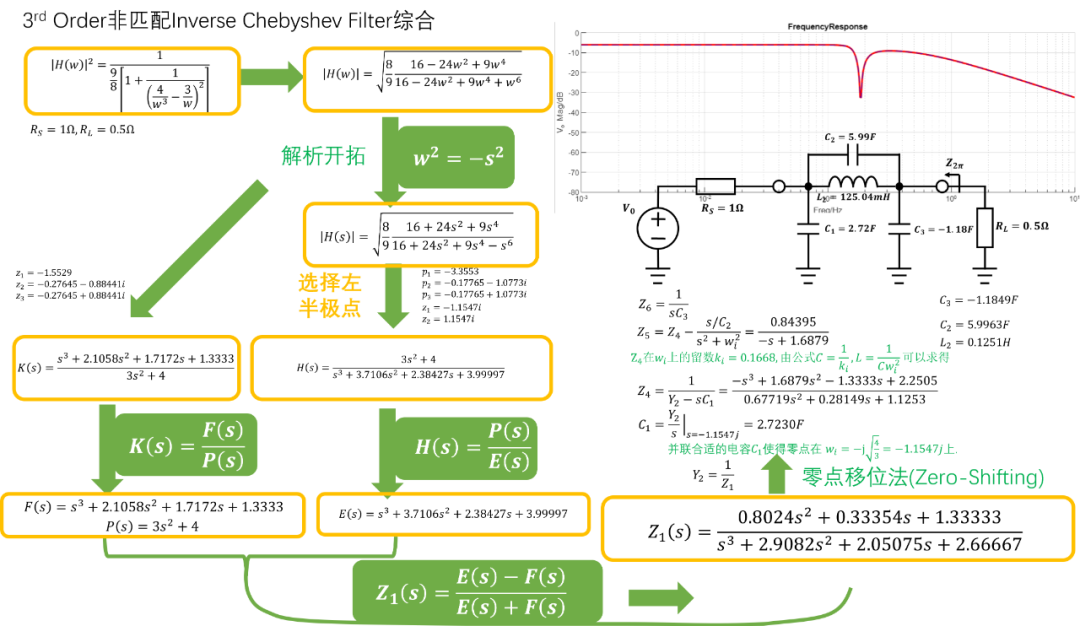
不同濾波器類型零極點對比
切比雪夫濾波器和巴特沃斯濾波器
切比雪夫濾波器和巴特沃斯濾波器無零點,屬于全極點濾波器。
切比雪夫濾波器極點排布為一個橢圓,橢圓長短半軸比越大紋波越大,這也是容易理解的,低頻的極點越靠近虛軸,那么極點所帶來的影響越大,紋波也越大。當紋波Ap特別小時,可以看到極點非常接近一個圓,這時濾波器就呈現巴特沃斯濾波器特性,所以從這點看巴特沃斯濾波器只是切比雪夫濾波器的一種特殊情況(即Ap=0,但是如果你用切比雪夫濾波器軟件來實現會出現錯誤,因為當紋波Ap=0dB時,截止頻率Fp=0Hz,這種情況下軟件會報錯)。
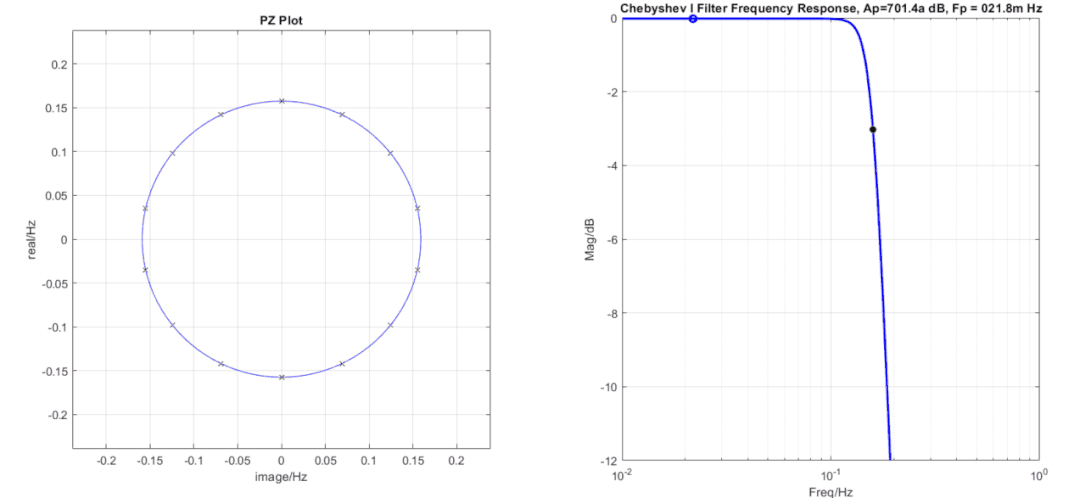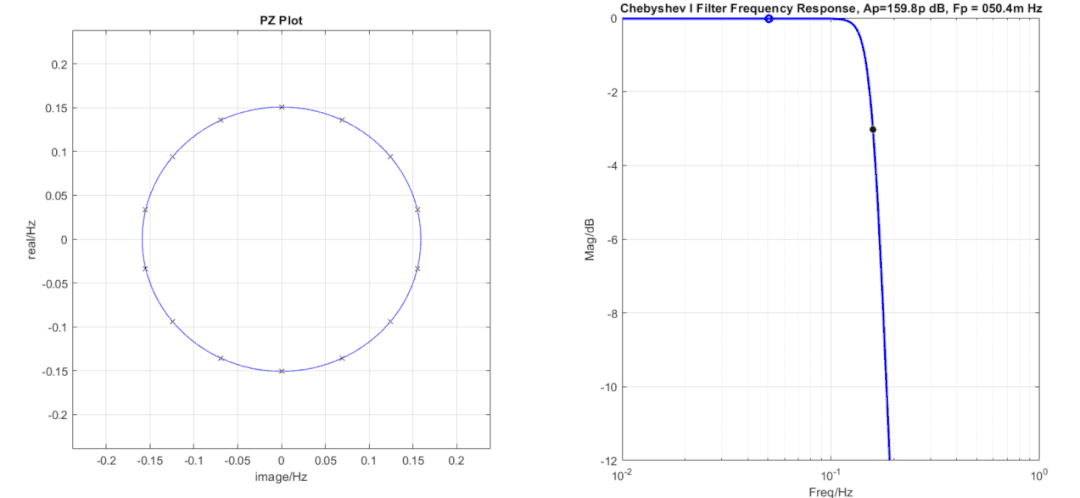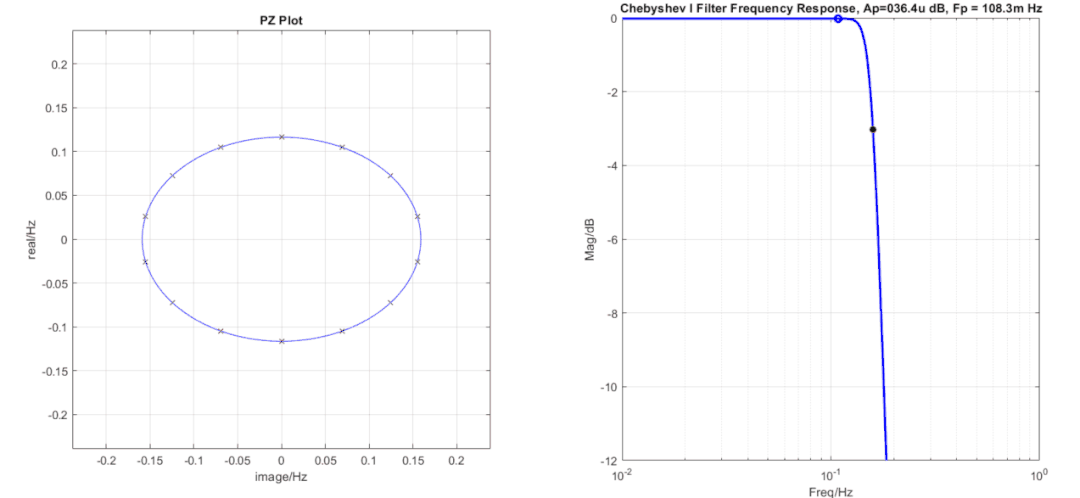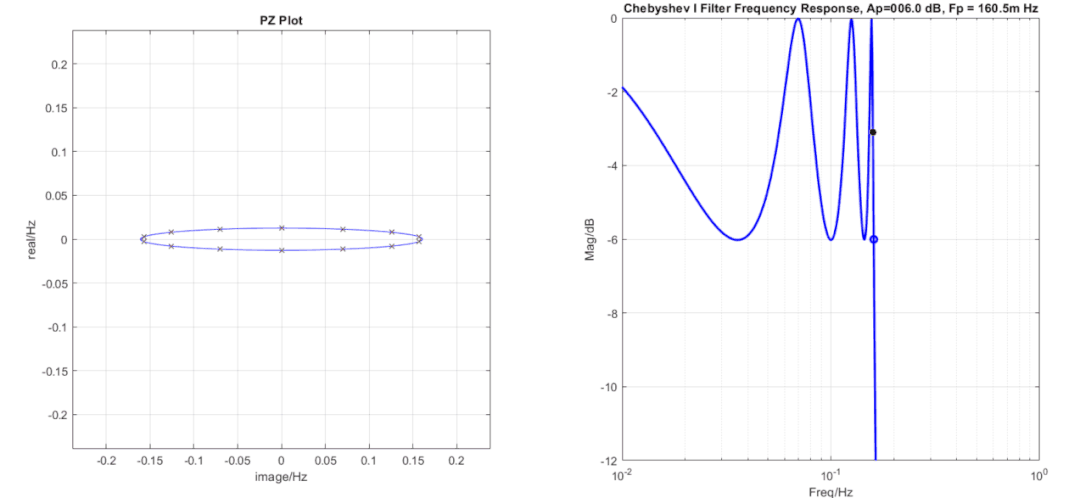
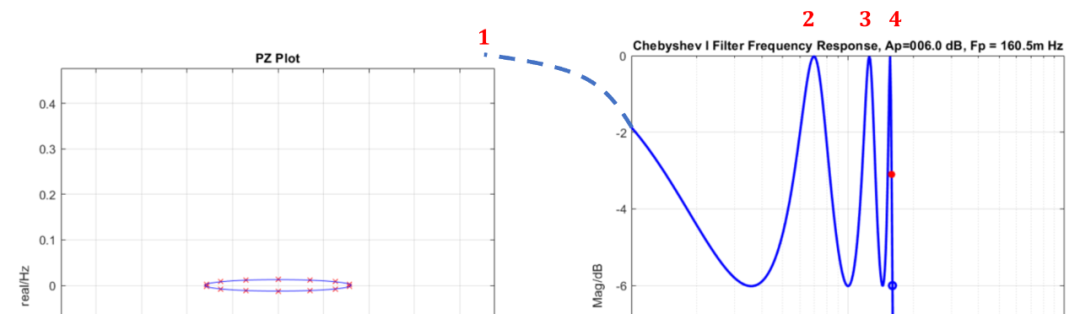
切比雪夫濾波器當階數和-3dB截止頻率位置一定時,不同紋波的濾波器其極點的虛軸坐標位置不變。利用這一點可以通過頻響曲線鼓包來推測濾波器階數,切比雪夫濾波器的紋波起伏是怎么來的呢,其中的衰減最小點是由極點帶來的,因為每個極點都會在對應的頻率點提供一個頻率鼓包,兩個頻率之間的位置上就有一個凹坑,頻響曲線上有多少個鼓包就有多少個對應的極點,如上圖中的曲線在頻率響應曲線上帶來了4個鼓包,那么就有4個極點對應,由于在負頻率上有另外一半,減去0頻率上的多算的一個,濾波器階數即為4*2-1=7階。
逆切比雪夫濾波器
與前面切比雪夫濾波器類似,逆切比雪夫濾波器的零極點動畫如下:

圖中的藍色虛線是對應的切比雪夫濾波器極點位置,是一個橢圓曲線,綠色虛線是巴特沃斯極點位置是一個圓,而逆切比雪夫濾波器的極點位置如圖紅色虛線所示,位置為切比雪夫濾波器極點關于圓的特殊對稱點,若以逆切比雪夫極點為起點過零點畫一條直線,那么這條直線必經過對應切比雪夫濾波器的一個極點,并且兩個極點到圓的距離呈現反比關系。
另外逆切比雪夫濾波器在阻帶衰減非常大時,這時零點位置比較遠,極點接近一個圓,這也反映了逆切比雪夫濾波器在通帶有最大平坦度這一特性。下圖所示的就是三種濾波器的零極點圖,只是這三個極點幾乎要重合為同一個圓了。
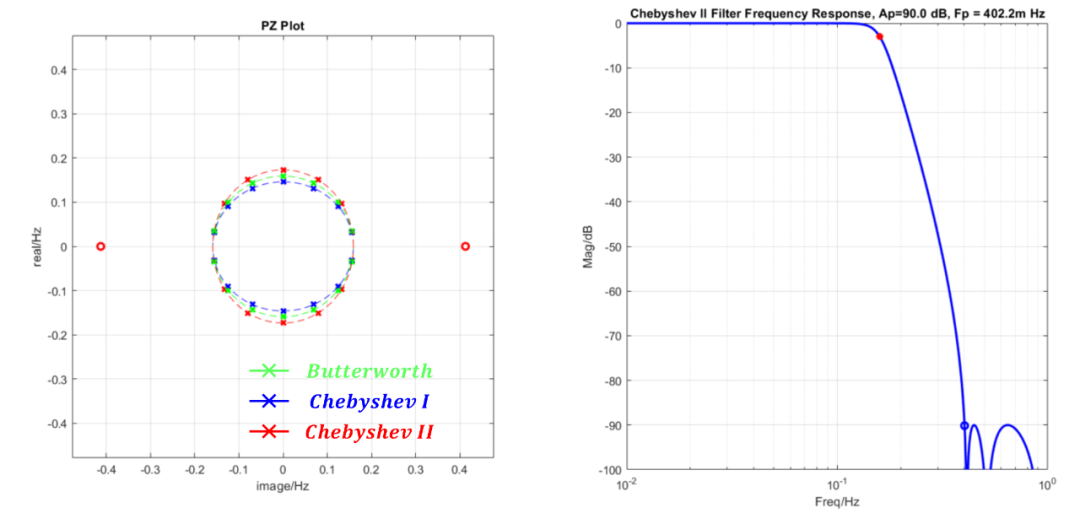
各位看官,到這里不知道大家有沒有考慮過若在上述情況下將極點位置由一個圓變為橢圓會怎么樣?是不是這樣我們既可以在通帶等紋波又可以阻帶等紋波?對了,這也是我們下一回將要講到的橢圓函數濾波器設計。
切比雪夫濾波器設計軟件
基于Matlab的appdesign工具開發了一套切比雪夫濾波器設計軟件,主要特點是:
支持切比雪夫濾波器(Chebyshev I)、逆切比雪夫濾波器(Chebyshev II, Inverse Chebyshev)、巴特沃斯濾波器(Butterworth)設計
支持4種不同濾波器通帶類型(LPF,HPF,BPF,BRF)設計
T型和PI型結構濾波器隨意切換
可以設置阻帶衰減決定濾波器階數
可以設置通帶衰減來綜合濾波器
可以隨意配置負載和終端阻抗,并支持一端接載(源端電阻短路,源端電流源,終端開路,終端短路)設計
可以幅頻響應分析、零極點分析、瞬態分析
可以顯示理想頻率響應、零極點和實際仿真的的頻率響應、零極點
可以支持實際標準器件逼近設計
切比雪夫LPF設計舉例
設計一款-3dB截止頻率為1GHz,7階低通Chebyshev濾波器,輸入輸出阻抗為50歐姆,設計過程如下:

最終設計參數如下:
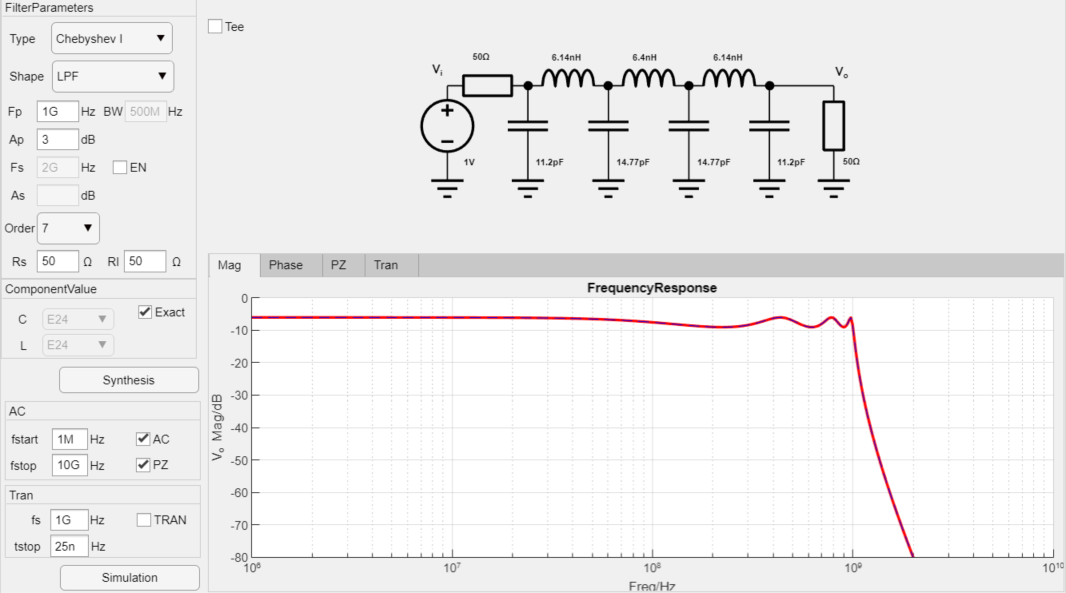
零極點仿真結果:
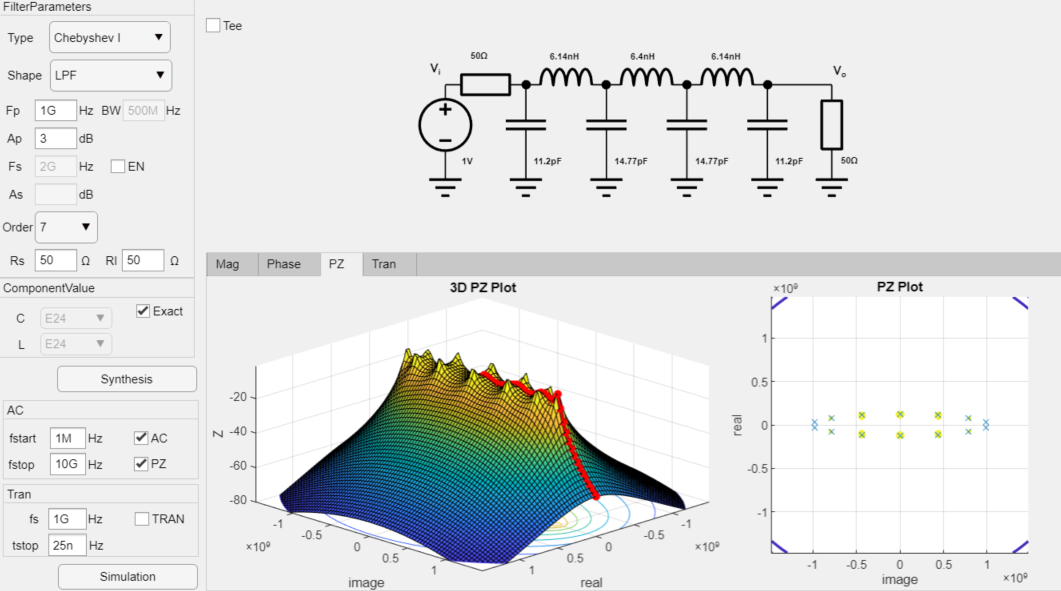
逆切比雪夫BPF設計舉例
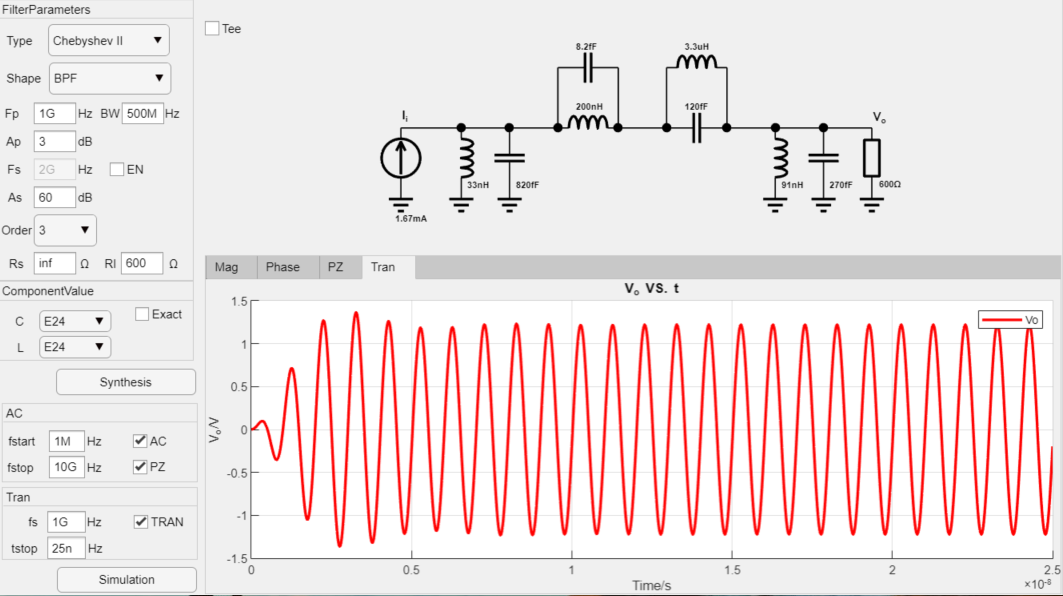
設計3階帶通逆切比雪夫濾波器(Chebyshev II),中心頻率為1GHz,帶寬為500MHz,電流輸入,輸出阻抗為600歐姆,并且選擇E24系列器件進行綜合,最后進行瞬態仿真,設計過程如下:

最終設計參數如下(可以看到使用實際的E24系列電感和電容設計帶通濾波器頻率響應和理論值偏差很大,這部分功能還有優化空間):
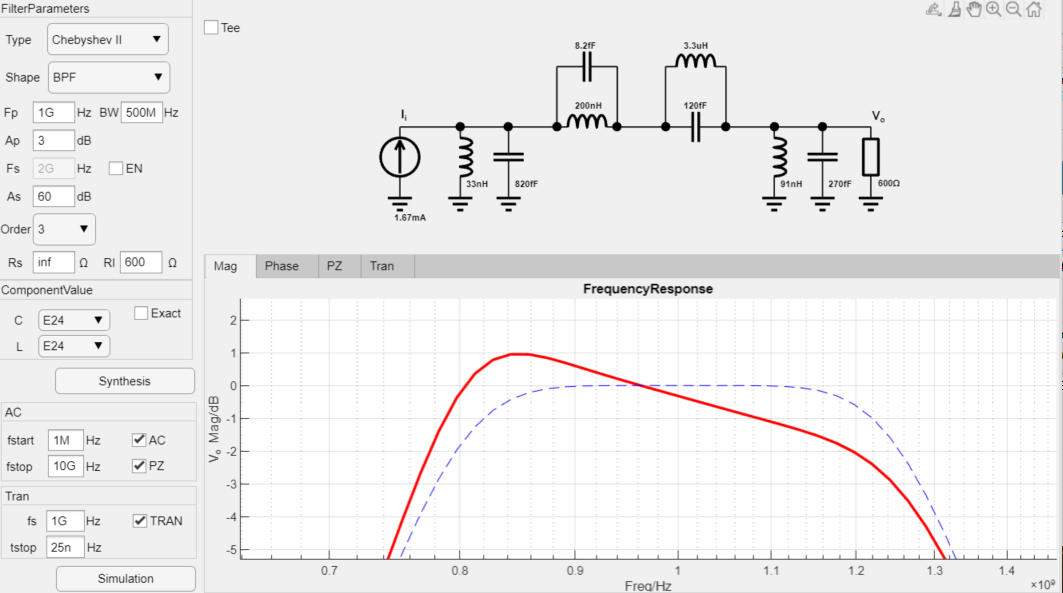
瞬態仿真結果:
程序的Matalb源碼已經上傳GitHub中(https://github.com/etools361/MatlabChebyshevFilterDesignApp.git),有興趣的同學可以下載試用體驗,當然也歡迎技術交流。
審核編輯:湯梓紅
-
濾波器
+關注
關注
160文章
7749瀏覽量
177735 -
Chebyshev
+關注
關注
0文章
4瀏覽量
7524
原文標題:模擬無源濾波器設計(六)-Chebyshev濾波器設計詳解
文章出處:【微信號:電路設計小工具,微信公眾號:電路設計小工具】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
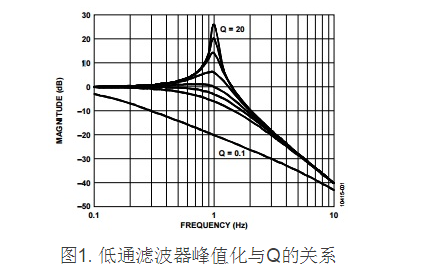
濾波器的截止頻率和品質因數詳解
切比雪夫濾波器模型建立及測試

labview中巴特沃斯濾波器和切比雪夫濾波器的異同
巴特沃斯濾波器與其他類型濾波器的比較
切比雪夫濾波器
采用感應濾波設計的雙調諧濾波器綜合技術

濾波器有幾種?四種濾波器之間對比詳解
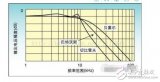
基于MATLAB的理想低通濾波器的設計
在連續時間域中比較Papoulis濾波器和Chebyshev濾波器





 切比雪夫濾波器的綜合設計
切比雪夫濾波器的綜合設計










評論