線性回歸是最簡單的機器學習模型之一。它通常不僅是學習數據科學的起點,也是構建快速簡單的最小可行產品( MVP )的起點,然后作為更復雜算法的基準。
一般來說,線性回歸擬合最能描述特征和目標值之間線性關系的直線(二維)或超平面(三維及三維以上)。該算法還假設特征的概率分布表現良好;例如,它們遵循高斯分布。
異常值是位于預期分布之外的值。它們導致特征的分布表現較差。因此,模型可能會向異常值傾斜,正如我已經建立的那樣,這些異常值遠離觀測的中心質量。自然,這會導致線性回歸發現更差和更有偏差的擬合,預測性能較差。
重要的是要記住,異常值可以在特征和目標變量中找到,所有場景都可能惡化模型的性能。
有許多可能的方法來處理異常值:從觀察值中刪除異常值,處理異常值(例如,將極端觀察值限制在合理值),或使用非常適合自己處理此類值的算法。本文重點介紹了這些穩健的方法。
安裝程序
我使用相當標準的庫:numpy、pandas、scikit-learn。我在這里使用的所有模型都是從scikit-learn的linear_model模塊導入的。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn import datasets from sklearn.linear_model import (LinearRegression, HuberRegressor, RANSACRegressor, TheilSenRegressor)
數據
鑒于目標是展示不同的魯棒算法如何處理異常值,第一步是創建定制的數據集,以清楚地顯示行為中的差異。為此,請使用scikit-learn中提供的功能。
首先創建一個包含 500 個觀察值的數據集,其中包含一個信息性特征。只有一個特征和目標,繪制數據以及模型的擬合。此外,指定噪聲(應用于輸出的標準差),并創建包含基礎線性模型系數的列表;也就是說,如果線性回歸模型適合生成的數據,系數會是多少。在本例中,系數的值為 64.6 。提取所有模型的系數,并使用它們來比較它們與數據的擬合程度。
接下來,用異常值替換前 25 個觀察值(占觀察值的 5% ),遠遠超出生成的觀察值的質量。請記住,先前存儲的系數來自沒有異常值的數據。包括他們會有所不同。
N_SAMPLES = 500 N_OUTLIERS = 25 X, y, coef = datasets.make_regression( n_samples=N_SAMPLES, n_features=1, n_informative=1, noise=20, coef=True, random_state=42 ) coef_list = [["original_coef", float(coef)]] # add outliers np.random.seed(42) X[:N_OUTLIERS] = 10 + 0.75 * np.random.normal(size=(N_OUTLIERS, 1)) y[:N_OUTLIERS] = -15 + 20 * np.random.normal(size=N_OUTLIERS) plt.scatter(X, y);
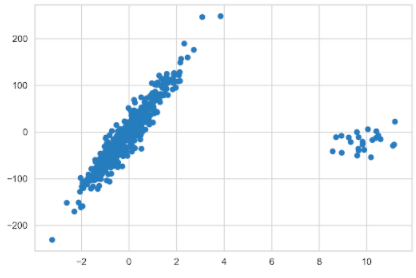
線性回歸
從良好的舊線性回歸模型開始,該模型可能受到異常值的高度影響。使用以下示例將模型與數據擬合:
lr = LinearRegression().fit(X, y) coef_list.append(["linear_regression", lr.coef_[0]])
然后準備一個用于繪制模型擬合的對象。plotline_X對象是一個 2D 數組,包含在生成的數據集指定的間隔內均勻分布的值。使用此對象獲取模型的擬合值。它必須是 2D 數組,因為它是scikit-learn中模型的預期輸入。然后創建一個fit_df數據框,在其中存儲擬合值,通過將模型擬合到均勻分布的值來創建。
plotline_X = np.arange(X.min(), X.max()).reshape(-1, 1) fit_df = pd.DataFrame( index = plotline_X.flatten(), data={"linear_regression": lr.predict(plotline_X)} )
準備好數據框架后,繪制線性回歸模型與具有異常值的數據的擬合圖。
fix, ax = plt.subplots() fit_df.plot(ax=ax) plt.scatter(X, y, c="k") plt.title("Linear regression on data with outliers");
圖 2 顯示了異常值對線性回歸模型的顯著影響。
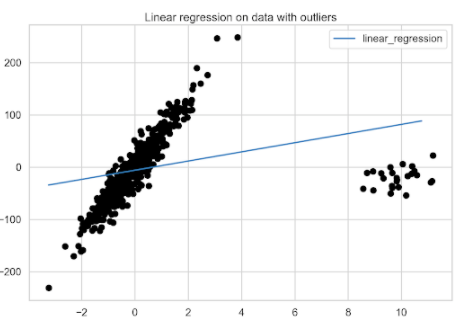
使用線性回歸獲得了基準模型。現在是時候轉向穩健回歸算法了。
Huber Regression
Huber regression 是穩健回歸算法的一個示例,該算法為被識別為異常值的觀察值分配較少的權重。為此,它在優化例程中使用 Huber 損耗。下面讓我們更好地了解一下這個模型中實際發生了什么。
Huber 回歸最小化以下損失函數:
其中,表示標準差,
表示特征集,
是回歸的目標變量,
是估計系數的向量,
是正則化參數。該公式還表明,根據 Huber 損失,對異常值的處理與常規觀測不同:
Huber 損失通過考慮殘差來識別異常值,用z表示。如果觀察被認為是規則的(因為殘差的絕對值小于某個閾值),然后應用平方損失函數。否則,將觀察值視為異常值,并應用絕對損失。話雖如此,胡伯損失基本上是平方損失函數和絕對損失函數的組合。
好奇的讀者可能會注意到,第一個方程類似于 Ridge regression ,即包括 L2 正則化。 Huber 回歸和嶺回歸的區別在于異常值的處理。
通過分析兩種常用回歸評估指標:均方誤差( MSE )和平均絕對誤差( MAE )之間的差異,您可能會認識到這種損失函數的方法。與 Huber 損失的含義類似,我建議在處理異常值時使用 MAE ,因為它不會像平方損失那樣嚴重地懲罰這些觀察值。
與前一點相關的是,優化平方損失會導致均值周圍的無偏估計,而絕對差會導致中值周圍的無偏估計。中位數對異常值的魯棒性要比平均值強得多,因此預計這將提供一個偏差較小的估計。
使用默認值 1.35 ,這決定了回歸對異常值的敏感性。 Huber ( 2004 )表明,當誤差服從正態分布且= 1 和= 1.35 時,相對于 OLS 回歸,效率達到 95% 。
對于您自己的用例,我建議使用網格搜索等方法調整超參數alpha和epsilon。
使用以下示例將 Huber 回歸擬合到數據:
huber = HuberRegressor().fit(X, y) fit_df["huber_regression"] = huber.predict(plotline_X) coef_list.append(["huber_regression", huber.coef_[0]])
圖 3 顯示了擬合模型的最佳擬合線。

RANSAC 回歸
隨機樣本一致性( RANSAC )回歸 是一種非確定性算法,試圖將訓練數據分為內聯(可能受到噪聲影響)和異常值。然后,它僅使用內聯線估計最終模型。
RANSAC 是一種迭代算法,其中迭代包括以下步驟:
從初始數據集中選擇一個隨機子集。
將模型擬合到選定的隨機子集。默認情況下,該模型是線性回歸模型;但是,您可以將其更改為其他回歸模型。
使用估計模型計算初始數據集中所有數據點的殘差。絕對殘差小于或等于所選閾值的所有觀察值都被視為內聯,并創建所謂的共識集。默認情況下,閾值定義為目標值的中值絕對偏差( MAD )。
如果足夠多的點被分類為共識集的一部分,則擬合模型保存為最佳模型。如果當前估計模型與當前最佳模型具有相同的內聯數,則只有當其得分更好時,才認為它更好。
迭代執行步驟的次數最多,或者直到滿足特殊停止標準。可以使用三個專用超參數設置這些標準。如前所述,最終模型是使用所有內部樣本估計的。
將 RANSAC 回歸模型與數據擬合。
ransac = RANSACRegressor(random_state=42).fit(X, y) fit_df["ransac_regression"] = ransac.predict(plotline_X) ransac_coef = ransac.estimator_.coef_ coef_list.append(["ransac_regression", ransac.estimator_.coef_[0]])
如您所見,恢復系數的過程有點復雜,因為首先需要使用estimator_訪問模型的最終估計器(使用所有已識別的內聯線訓練的估計器)。由于它是一個LinearRegression對象,請像前面一樣繼續恢復系數。然后,繪制 RANSAC 回歸擬合圖(圖 4 )。
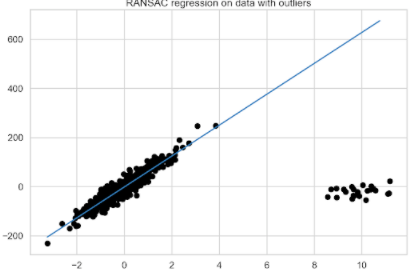
使用 RANSAC 回歸,您還可以檢查模型認為是內聯值和離群值的觀察值。首先,檢查模型總共識別了多少異常值,然后檢查手動引入的異常值中有多少與模型的決策重疊。訓練數據的前 25 個觀察值都是引入的異常值。
inlier_mask = ransac.inlier_mask_
outlier_mask = ~inlier_mask
print(f"Total outliers: {sum(outlier_mask)}")
print(f"Outliers you added yourself: {sum(outlier_mask[:N_OUTLIERS])} / {N_OUTLIERS}")
運行該示例將打印以下摘要:
Total outliers: 51 Outliers you added yourself: 25 / 25
大約 10% 的數據被確定為異常值,所有引入的觀察結果都被正確歸類為異常值。然后可以快速將內聯線與異常值進行比較,以查看標記為異常值的其余 26 個觀察值。
plt.scatter(X[inlier_mask], y[inlier_mask], color="blue", label="Inliers")
plt.scatter(X[outlier_mask], y[outlier_mask], color="red", label="Outliers")
plt.title("RANSAC - outliers vs inliers");
圖 5 顯示,距離原始數據的假設最佳擬合線最遠的觀測值被視為異常值。
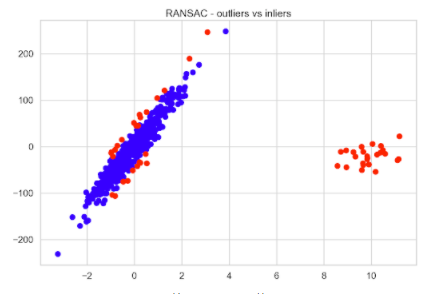
泰爾森回歸
scikit-learn中可用的最后一種穩健回歸算法是 Theil-Sen regression 。這是一種非參數回歸方法,這意味著它不假設基礎數據分布。簡而言之,它涉及在訓練數據子集上擬合多元回歸模型,然后在最后一步聚合系數。
下面是算法的工作原理。首先,它計算從訓練集 X 中的所有觀察值創建的大小為 p (超參數n_subsamples)的子集上的最小二乘解(斜率和截距)。如果計算截距(可選),則必須滿足以下條件p 》= n_features + 1。直線的最終斜率(可能還有截距)定義為所有最小二乘解的(空間)中值。
該算法的一個可能缺點是計算復雜度,因為它可以考慮等于n_samples choose n_subsamples的最小二乘解總數,其中n_samples是 X 中的觀測數。鑒于這一數字可能迅速擴大,可以做幾件事:
在樣本數量和特征方面,只對小問題使用該算法。然而,由于明顯的原因,這可能并不總是可行的。
調整n_subsamples超參數。值越低,對異常值的魯棒性越高,但效率越低,而值越高,魯棒性越低,效率越高。
使用max_subpopulation超參數。如果n_samples choose n_subsamples的總值大于max_subpopulation,則該算法僅考慮給定最大大小的隨機子種群。自然,僅使用所有可能組合的隨機子集會導致算法失去一些數學特性。
此外,請注意,估計器的穩健性隨著問題的維數迅速降低。要了解這在實踐中的效果,請使用以下示例估計泰爾森回歸:
theilsen = TheilSenRegressor(random_state=42).fit(X, y) fit_df["theilsen_regression"] = theilsen.predict(plotline_X) coef_list.append(["theilsen_regression", theilsen.coef_[0]])
模型比較
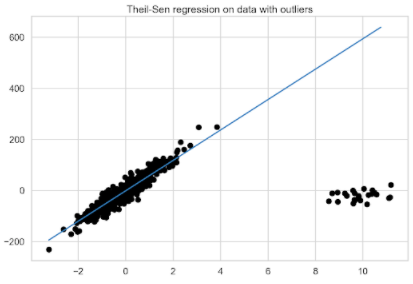
到目前為止,已經對包含異常值的數據擬合了三種穩健回歸算法,并確定了各個最佳擬合線。現在是進行比較的時候了。
從圖 7 的目視檢查開始。為了顯示太多行,未打印原始數據的擬合行。然而,考慮到大多數數據點的方向,很容易想象它是什么樣子。顯然, RANSAC 和泰爾森回歸得到了最準確的最佳擬合線。

圖 7 。所有考慮的回歸模型的比較
更準確地說,請查看估計系數。表 1 顯示, RANSAC 回歸結果最接近原始數據之一。有趣的是, 5% 的異常值對正則線性回歸擬合的影響有多大。
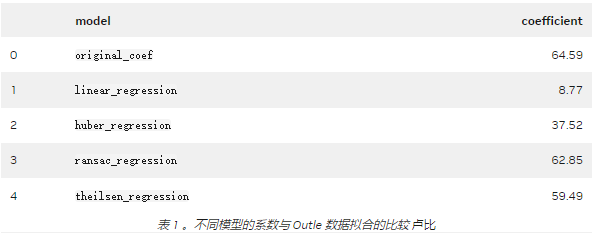
你可能會問哪種穩健回歸算法最好?通常情況下,答案是“視情況而定”以下是一些指導原則,可以幫助您找到適合您具體問題的正確模型:
一般來說,在高維環境中進行穩健擬合是困難的。
與泰爾·森和蘭薩克不同的是,休伯回歸并沒有試圖完全過濾掉異常值。相反,它會減少它們對貼合度的影響。
Huber 回歸應該比 RANSAC 和 Theil-Sen 更快,因為后者適用于較小的數據子集。
泰爾森和 RANSAC 不太可能像 使用默認超參數的 Huber 回歸。
RANSAC 比泰爾森更快,并且隨著樣本數的增加,其擴展性更好。
RANSAC 應該更好地處理 y 方向上的大異常值,這是最常見的場景。
考慮到前面的所有信息,您還可以根據經驗對所有三種穩健回歸算法進行實驗,看看哪一種最適合您的數據。
關于作者
Eryk Lewinson 是一位數據科學家,有定量金融方面的背景。在他的職業生涯中,他曾為兩家咨詢公司工作,一家金融科技公司,最近為荷蘭最大的在線零售商工作。在他的工作中,他使用機器學習為公司生成可操作的見解。
審核編輯:郭婷
-
機器學習
+關注
關注
66文章
8377瀏覽量
132406 -
數據集
+關注
關注
4文章
1205瀏覽量
24641
發布評論請先 登錄
相關推薦
回歸算法有哪些,常用回歸算法(3種)詳解
TensorFlow實現簡單線性回歸
TensorFlow實現多元線性回歸(超詳細)
使用PyMC3包實現貝葉斯線性回歸
使用KNN進行分類和回歸
基于支持向量回歸的交易模型的穩健性策略
基于Weierstrass逼近定理在非線性回歸模型中應用
8種用Python實現線性回歸的方法對比分析_哪個方法更好?
數據清洗、缺失值填充和異常值處理
靜電放電ESD三種模型及其防護設計





 使用三種穩健線性回歸模型處理異常值
使用三種穩健線性回歸模型處理異常值
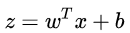










評論