導讀:自9月以來,我的《教你Matlab有限元編程對懸臂梁進行受力分析》原創文章發布以來,我的精品課《Matlab有限元編程從入門到精通10講》受到了越來越多的工程師朋友的關注,已超過50多人已經訂閱學習,歡迎大家加入訂閱用戶交流群一起討論Matlab有限元編程那些事(哈哈哈,為大家答疑和分享資料)。
今天,我接著分享Matlab有限元編程專業技能。之前的課程我們學習了一維梁單元,二維平面單元,三維板殼單元的matlab有限元編程,本次案例主要講解如何用matlab實現針對四面體單元劃分的三維結構進行有限元編程,具體案例是一個懸臂梁受集中荷載的問題。圖1為本案例Matlab編程計算得到的結果。主要內容涉及四面體單元的有限元基本理論的推導,主要是單元剛度矩陣的推導,此外還包括等參單元和Hammer數值積分以及三維問題的后處理計算。
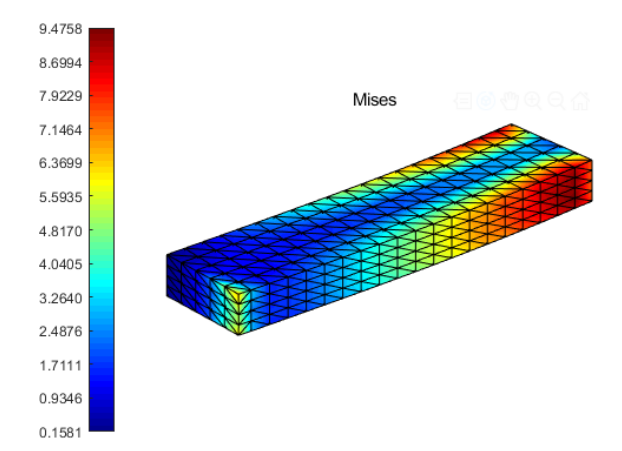
圖1 懸臂梁受集中荷載的應力云圖
一個完整的有限元程序基本組成部分包括前處理模塊、分析主程序模塊和后處理模塊。在前處理模塊中,實現節點坐標輸入、單元節點編號、網絡劃分以及邊界條件輸入等工作;在分析主程序模塊中,求解整體剛度方程;在后處理模塊中,實現結果顯示、數據輸出等工作。
對應的有限元法的基本步驟:
(1)幾何域離散,獲得標準化的單元; (2)通過能量原理(虛功原理或最小勢能原理,獲得單元剛度方程; (3)單元的集成(裝配); (4)處理位移邊界條件; (5)計算位移場;
(6)計算單元的其他物理量(應力應變)。
這幾步中,最核心的內容是單元研究,具體包括:
(1)節點描述(不同坐標系節點坐標的變化); (2)場描述(位移場,應變場,應力場,形函數);
(3)單元剛度方程(基于能量原理推導)。
需要說明的是后文的四面體單元有限元方程的推導過程是基于等參單元的基本理論從局部坐標(自然坐標、體積坐標)出發來推導四面體單元的剛度矩陣,因為這樣做比較規范自然,推導過程也適用于其他類型單元。但是因為四面體單元相對簡單也可以直接從直角坐標(全局坐標)進行推導,具體推導過程可參考清華大學曾攀老師的課程,直接從直角坐標(全局坐標)進行推導的過程省去了等參單元雅各比矩陣呀等坐標系映射的各種概念,理解起來相對容易。
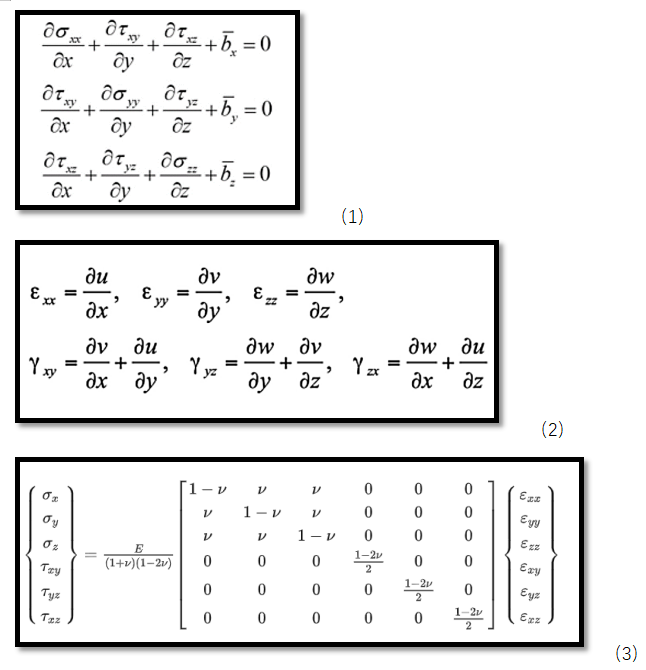
公式(1)-(3)為彈性力學中三維空間彈性問題的完整描述,分別是空間問題的平衡方程、幾何方程、物理方程,這是我們推導有限元方程的基礎。這些公式會在后面的有限元方程推導過程中用到。
四面體單元的坐標描述涉及了等參單元的概念,在有限元方法中,若要離散邊界為曲線或曲面的求解域,需要建立將形狀規則的單元變換為邊界為曲線或曲面的單元的方法,在有限元法中對應此問題所采用的變換方法是等參變換,即單元幾何形狀的變換和單元內場函數采用相同數目的節點及相同的插值函數進行變換。四面體單元的參數坐標就是體積坐標,體積坐標的定義如圖2所示。
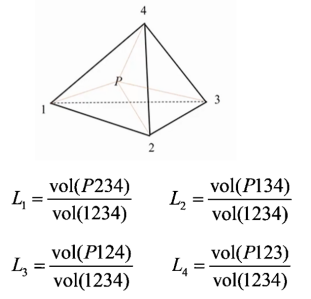
圖2 四面體單元體積坐標的定義
參數坐標系下的形函數等于對應的體積坐標,四個節點對應四個形函數,如下式,
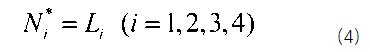
這樣就實現了自然坐標系和物理坐標系下的坐標映射,如下式,
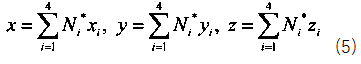
同樣形函數也可以用于物理場的插值,公式(6)是位移場的插值表達式。
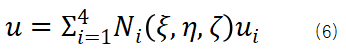
有了位移場插值的表達式就可以通過公式(2)-(3)的幾何方程和物理方程推導應變場和應力場的有限元表達式,但是公式(2)的幾何方程中存在對于xy也就是物理坐標系下的偏導數,代入公式(6)后也就是形函數對物理坐標的偏導數,因為我們的形函數是在自然坐標系下定義的,是關于ξ, η, ζ的函數,想要知道他對x,y的偏導,這里利用了鏈式求導法則,即可建立如下式(7)所示的形函數對自然坐標的物理坐標偏導數的映射關系。中間的這個矩陣就叫Jacob矩陣。
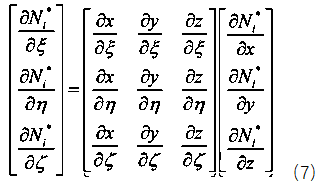
如何求Jacob矩陣呢?將公式(5)代入公式(7)可以得到如下式(8)所示的自然坐標偏導矩陣乘以一個坐標矩陣,
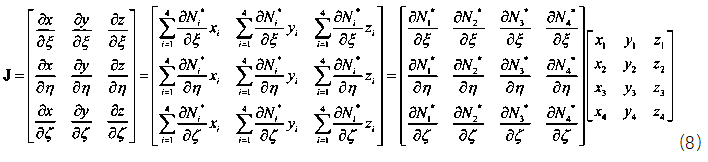
得到jacob矩陣后求逆,再乘以自然坐標偏導矩陣就可以得到形函數對物理坐標的導數。如下式(9),
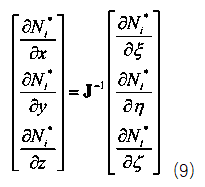
上述形函數對物理坐標的導數的求解過程對應的matlab代碼如下:
function [NDxyz,JacobiDET] = ShapeFunction(ElementNodeCoordinate) %計算形函數及形函數對局部坐標ksi eta zeta的導數 NDL = [-1 1 0 0;-1 0 1 0;-1 0 0 1];%3*4 [N1Dksi N2Dksi N3Dksi N4Dksi;N1Deta N2Deta N3Deta N4Deta……] Jacobi = NDL*ElementNodeCoordinate;%計算雅可比矩陣3*4 4*3 JacobiDET = det(Jacobi);%計算雅可比行列式3*3 [DxDksi DyDksi DzDksi;DxDeta…… JacobiINV=inv(Jacobi);%對雅可比行列式求逆3*3 NDxyz=JacobiINV*NDL;%利用雅可比行列式的逆計算形函數對結構坐標的導數[DN1Dx DN2Dx DN3Dx;DN1Dy DN2Dy DN3Dy;……] end這樣求出形函數對物理坐標的導數后就可以代入公式(2)幾何方程求出應變場矩陣B,經過能量原理的推導可以得到單元剛度矩陣的表達式,注意剛度矩陣的表達式是一個積分的運算,由于被積函數較為復雜,如果代數積分進行計算要消耗大量的計算資源,因此有限元理論中引入數值積分,即我們熟悉的高斯積分和hammer積分,對于直角坐標系我們采用高斯積分,對于面積或者體積坐標系我們采用hammer數值積分,具體這兩類積分的原理大家可以參考相關數值積分教材即可,這里我們只利用hammer數值積分的結論。四面體單元具體的數值積分公式如下:
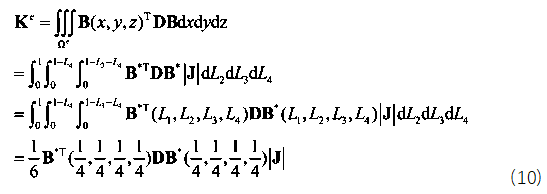
其中,對應的B矩陣如下式所示:
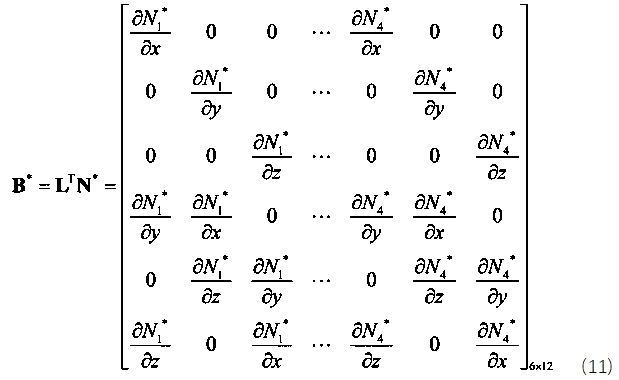
單元剛度矩陣確定好之后,將其按照自由度索引組裝到全局剛度矩陣中,組裝的核心思想就是確定好每個單元中的每個節點中的每個自由度在整體剛度矩陣中的位置即可。
整體剛度矩陣確定之后,就是荷載向量p的定義,這個很簡單,只要依次確定每個節點每個自由度的外力荷載即可。
剛度矩陣和荷載向量確定后接下來就是邊界條件的施加,大家最熟悉的可能就是直接劃行劃列的方法,這個方法的弊端在于劃去自由度為零的行列之后,整體單元剛度矩陣的編號以及自由度編號都會改變,對于大規模計算非常不方便,影響計算效率。為了解決這個問題出現了乘大數法和置一法,置一法只能解決零邊界問題,乘大數法可以解決零邊界和非零邊界,應用非常廣泛。邊界條件的施加這里我們采用乘大數法。針對邊界條件采用乘大數法施加邊界的方式為:在自由度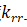 上乘以一個很大的數a,然后在相應的外力向量對應的自由度上乘以
上乘以一個很大的數a,然后在相應的外力向量對應的自由度上乘以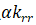 ,具體如下式(22)所示
,具體如下式(22)所示
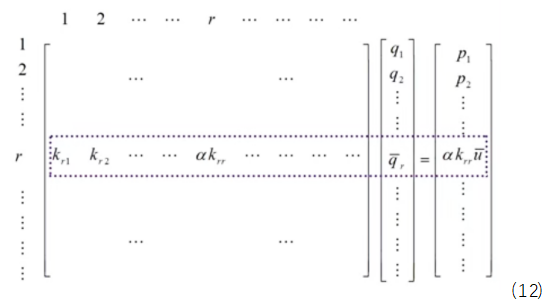
為了驗證乘大數法的可靠性,將對應行列寫成代數表達式的形式,如下式所示
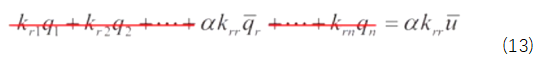
考慮到遠大于,所以公式(13)可以寫成,
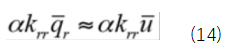
即可得到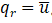 。可見乘大數法與實際邊界條件是等價的。
。可見乘大數法與實際邊界條件是等價的。
施加了邊界條件的剛度矩陣K與荷載矩陣p之后,可直接利用matlab中的高斯消去法 計算符“”,完成位移的求解,即u=Kp。
求出節點位移之后通常我們做受力分析時還會需要知道應力應變的分布情況,具體通過下述公式求解:
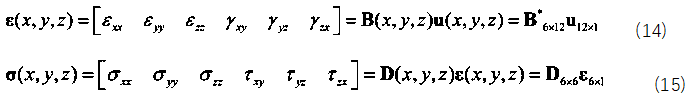
對應的提取應力和應變的后處理代碼如下:
% 計算形函數導數
[NDxyz, ~] = ShapeFunction(ElementNodeCoordinate);%[DN1Dx DN2Dx DN3Dx;DN1Dy DN2Dy DN3Dy;……]
ElementNodeDisplacement=U(ElementNodeDOF);%12*1 節點位移列陣
ElementNodeDisplacement=reshape(ElementNodeDisplacement,Dof,4);%3*4
% 計算單元應變 Strain3_3 3*3的應變矩陣
Strain3_3=ElementNodeDisplacement*NDxyz';%高斯積分點處應變 3*4 4*3
%把單元應變矩陣改寫成6*1
Strain=[Strain3_3(1,1) Strain3_3(2,2) Strain3_3(3,3) ...
Strain3_3(1,2)+Strain3_3(2,1)....
Strain3_3(2,3)+Strain3_3(3,2) Strain3_3(1,3)+Strain3_3(3,1)]';
Stress(1:6,1) = D*Strain;%高斯積分點處應變
利用繪圖命令Patch我們可以得到如圖1所示的應力云圖。另外計算得到的變形和位移云圖如圖3-4所示。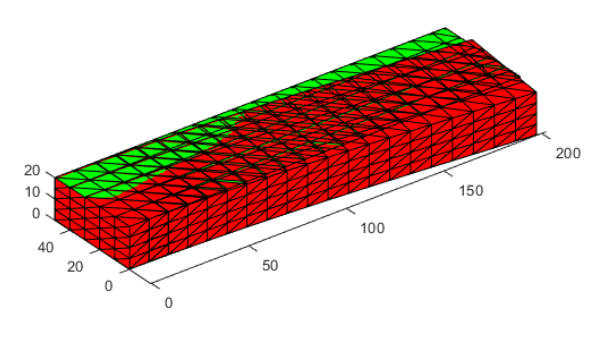
圖3 變形前后的網格對比
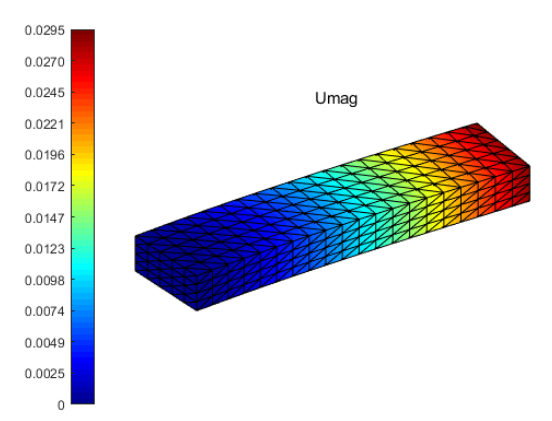
圖4 位移云圖
審核編輯:劉清
-
matlab
+關注
關注
182文章
2963瀏覽量
230195 -
矩陣
+關注
關注
0文章
422瀏覽量
34504 -
信號處理模塊
+關注
關注
1文章
6瀏覽量
6997
原文標題:案例實操:四面體單元懸臂梁的Matlab有限元編程過程講解
文章出處:【微信號:sim_ol,微信公眾號:模擬在線】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
MATLAB有限元分析與應用
HFSS 仿真算法及其應用場景詳解:有限元算法、積分方程算法、PO算法
利用有限元方法對280M1-2型三相異步電機的法蘭結構強度進行分析校核
膜厚對四面體非晶碳膜機械性能的影響
兩可傾瓦軸承負荷傳感器結構三維有限元分析
人體面骨三維有限元模型重構及碰撞分析
如何使用Matlab進行有限元分析和硬盤的選購與使用資料說明
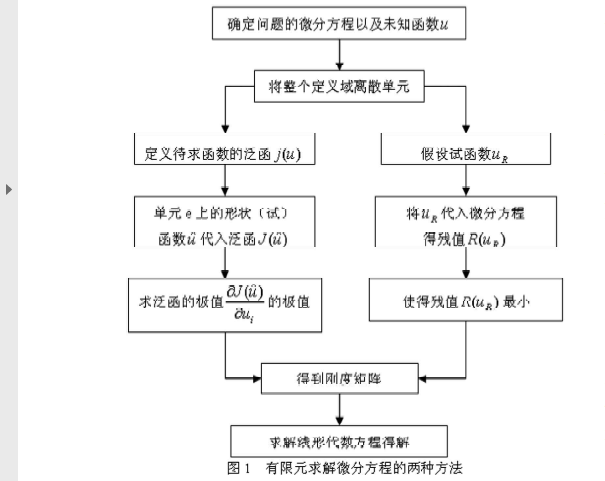
怎樣在3d CAD中創建常規四面體




 如何用matlab實現針對四面體單元劃分的三維結構進行有限元編程
如何用matlab實現針對四面體單元劃分的三維結構進行有限元編程












評論