FPGA浮點轉定點運算、除法轉乘法運算以及運算誤差分析
FPGA在常規運算時不能進行浮點運算,只能進行定點整型運算,在處理數據的小數乘加運算和除法運算時FPGA一般是無能為力的,其中一種常用的處理方法就是數據進行浮點到定點的轉換。
浮點數轉化為定點數一般有兩種方法:
浮點數直接乘以一個數值。浮點小數(X)到定點數據(Xq)的轉換其實很簡單,就是把浮點小數乘以一個很大的2的n次冪的數據Xq=X*2^n,來把小數轉化為整數,然后再進行數據的乘加運算,運算結果通過移位來得到實際對應的理論數據結果。
直接把浮點數轉化為有符號的二進制小數用SxQn來表示,然后進行乘加運算,運算結果通過移位來得到實際對應的理論數據結果。
通過上述兩種方法運算能完成浮點到定點乘加運算的結果,但是上述兩種方法存在一定的問題:
存在浮點小數(X)進行整數轉化定點數據(Xq)后依然還是一個小數的情況。
浮點數轉化為二進制數存在數據位寬激增情況,使得SxQn的數據位寬變大。
數據運算存在一定的截位誤差,這部分誤差只能減小而不能消除。
浮點到定點數據轉化后數據位寬變大,占用邏輯資源增加。
在實際使用時由于直接把浮點數轉化為有符號的二進制小數用SxQn來表示這種方法局限性較多,近而大都采用浮點數直接乘以一個數值這種方式,但是這種方式使用時需要注意截位誤差和量化誤差。
第一種浮點數直接乘以一個數值方法具體過程如下:
浮點數(x)轉換為定點數(xq):xq=(int)x2^Q 定點數(xq)轉換浮點數(x):x= (float)xq2^(-Q) 比如,16進制數2000H,用Q0表示就是8192;若用Q15表示,則為0.25。 下面介紹Q格式運算中Q值的確定:
(1)定點加減法:需要轉換成相同Q格式才能加減 (2)定點乘法:不同Q格式的數據相乘,相當于Q值相加 (3)定點除法:不同Q格式的數據相除,相當于Q值相減 (4)定點左移:相當于Q值增加 (5)定點右移:相當于Q值減少 比如,Q15表示的4000H(浮點數0.5)乘以Q15表示的4000H,4000H×4000H=1000 0000H,乘完之后Q值變為15+15=30,即結果為0.01B,即為浮點數0.25。 對應浮點數的除法運算時是把除法轉換成乘法運算來實現。即分子/分母(A/B)轉化為A*(1/B),這時會面臨B是固定值和變值兩種情況 1、如果B是固定值利用這種方式即可把(1/B)轉化為定點數,然后進行乘法運算,這樣計算速率較塊,且通過合理的選擇放大倍數來減小數據的誤差。 2、如果對應B不是固定值,那么就將B變為對應位寬的整數,然后再進行數據的乘法運算。 數據的誤差來源于浮點轉化為定點時截位和運算結果截位引起的,這里可以通過常用的截位方式來實現截位。 常見的截位方式有:
1、負數直接截位后+1,就是所有數都按絕對值取floor 2、Truncate:直接截位,就是正數取floor,負數按絕對值取ceil 3、Rounding:舍入截位,就是所有數按絕對值取四舍五入
-
FPGA
+關注
關注
1626文章
21665瀏覽量
601806 -
數據
+關注
關注
8文章
6888瀏覽量
88826
原文標題:FPGA浮點轉定點運算、除法轉乘法運算以及運算誤差分析
文章出處:【微信號:gh_9d70b445f494,微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
【安富萊——DSP教程】第7章 DSP定點數和浮點數(重要)
第7章 DSP定點數和浮點數
verilog程序定點數的資料
功能函數中的浮點數轉換為定點數
定點數和浮點數的區別是什么
請問ADSP-21469的匯編指令集ISA/VISA中有沒有專門用來進行浮點數和定點數轉換的指令?
功能:雙字節十六進制定點數轉換成格式化浮點數
在FPGA里浮點數與定點數表示法原理展示

單片機浮點數運算的源碼設計

定點數和浮點數在STM32單片機中使用傅里葉(FFT)變換的理解

定點數和浮點數的概念 浮點數二進制序列與指數表達式之間的轉化
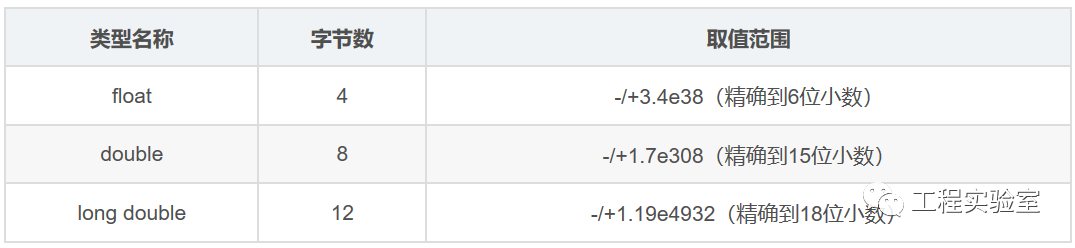




 FPGA浮點數轉化為定點數方法
FPGA浮點數轉化為定點數方法










評論