美團數(shù)據(jù)庫平臺研發(fā)組,面臨日益急迫的數(shù)據(jù)庫異常發(fā)現(xiàn)需求,為了更加快速、智能地發(fā)現(xiàn)、定位和止損,我們開發(fā)了基于AI算法的數(shù)據(jù)庫異常檢測服務(wù)。本文從特征分析、算法選型、模型訓(xùn)練與實時檢測等維度介紹了我們的一些實踐和思考,希望為從事相關(guān)工作的同學(xué)帶來一些啟發(fā)或者幫助。
1. 背景
2. 特征分析
2.1 找出數(shù)據(jù)的變化規(guī)律
3. 算法選型
3.1 分布規(guī)律與算法選擇
3.2 案例樣本建模
4. 模型訓(xùn)練與實時檢測
4.1 數(shù)據(jù)流轉(zhuǎn)過程
4.2 異常檢測過程
5. 產(chǎn)品運營
6. 未來展望
7. 附錄
7.1 絕對中位差
7.2 箱形圖
7.3 極值理論
1. 背景
數(shù)據(jù)庫被廣泛用于美團的核心業(yè)務(wù)場景上,對穩(wěn)定性要求較高,對異常容忍度非常低。因此,快速的數(shù)據(jù)庫異常發(fā)現(xiàn)、定位和止損就變得越來越重要。針對異常監(jiān)測的問題,傳統(tǒng)的固定閾值告警方式,需要依賴專家經(jīng)驗進行規(guī)則配置,不能根據(jù)不同業(yè)務(wù)場景靈活動態(tài)調(diào)整閾值,容易讓小問題演變成大故障。 而基于AI的數(shù)據(jù)庫異常發(fā)現(xiàn)能力,可以基于數(shù)據(jù)庫歷史表現(xiàn)情況,對關(guān)鍵指標(biāo)進行7*24小時巡檢,能夠在異常萌芽狀態(tài)就發(fā)現(xiàn)風(fēng)險,更早地將異常暴露,輔助研發(fā)人員在問題惡化前進行定位和止損。基于以上這些因素的考量,美團數(shù)據(jù)庫平臺研發(fā)組決定開發(fā)一套數(shù)據(jù)庫異常檢測服務(wù)系統(tǒng)。接下來,本文將會從特征分析、算法選型、模型訓(xùn)練與實時檢測等幾個維度闡述我們的一些思考和實踐。
2. 特征分析
2.1 找出數(shù)據(jù)的變化規(guī)律
在具體進行開發(fā)編碼前,有一項非常重要的工作,就是從已有的歷史監(jiān)控指標(biāo)中,發(fā)現(xiàn)時序數(shù)據(jù)的變化規(guī)律,從而根據(jù)數(shù)據(jù)分布的特點選取合適的算法。以下是我們從歷史數(shù)據(jù)中選取的一些具有代表性的指標(biāo)分布圖:
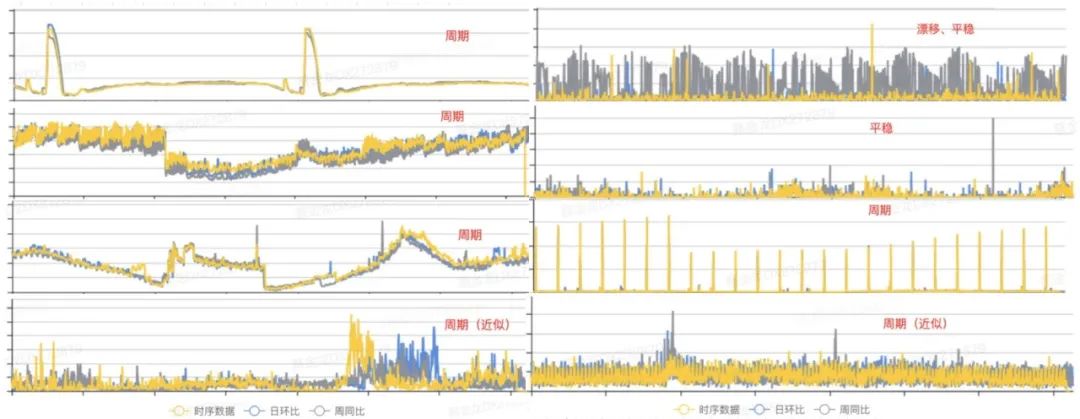
圖1 數(shù)據(jù)庫指標(biāo)形態(tài) 從上圖我們可以看出,數(shù)據(jù)的規(guī)律主要呈現(xiàn)三種狀態(tài):周期、漂移和平穩(wěn)[1]。因此,我們前期可以針對這些普遍特征的樣本進行建模,即可覆蓋大部分場景。接下來,我們分別從周期性、漂移性和平穩(wěn)性這三個角度進行分析,并討論算法設(shè)計的過程。
2.1.1 周期性變化
在很多業(yè)務(wù)場景中,指標(biāo)會由于早晚高峰或是一些定時任務(wù)引起規(guī)律性波動。我們認(rèn)為這屬于數(shù)據(jù)的內(nèi)在規(guī)律性波動,模型應(yīng)該具備識別出周期性成分,檢測上下文異常的能力。對于不存在長期趨勢成分的時序指標(biāo)而言,當(dāng)指標(biāo)存在周期性成分的情況下,,其中T代表的是時序的周期跨度。可通過計算自相關(guān)圖,即計算出t取不同值時 的值,然后通過分析自相關(guān)峰的間隔來確定周期性,主要的流程包括以下幾個步驟:
提取趨勢成分,分離出殘差序列。使用移動平均法提取出長期趨勢項,跟原序列作差得到殘差序列(此處周期性分析與趨勢無關(guān),若不分離趨勢成分,自相關(guān)將顯著受到影響,難以識別周期)。
計算殘差的循環(huán)自相關(guān)(Rolling Correlation)序列。通過循環(huán)移動殘差序列后,與殘差序列進行向量點乘運算來計算自相關(guān)序列(循環(huán)自相關(guān)可以避免延遲衰減)。
根據(jù)自相關(guān)序列的峰值坐標(biāo)來確定周期T。提取自相關(guān)序列的一系列局部最高峰,取橫坐標(biāo)的間隔為周期(如果該周期點對應(yīng)的自相關(guān)值小于給定閾值,則認(rèn)為無顯著周期性)。
具體過程如下:
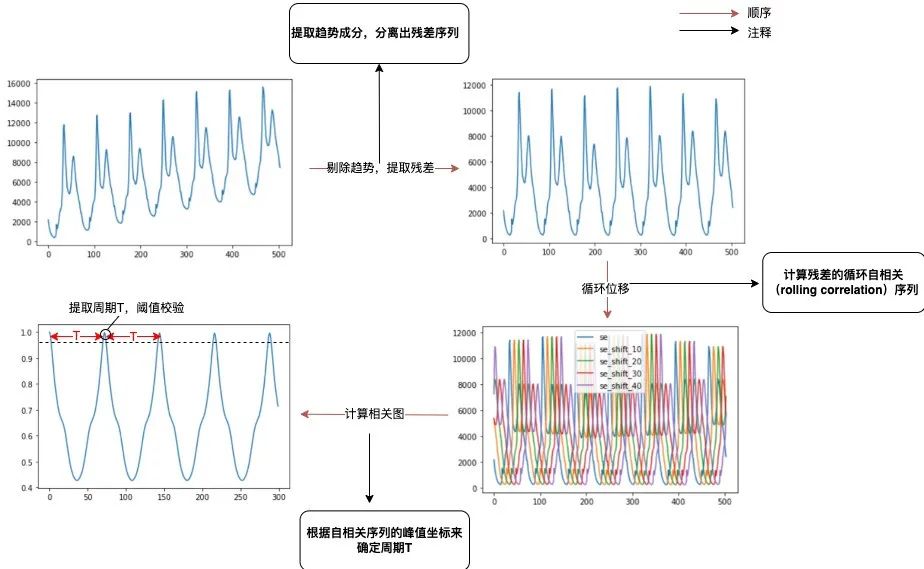
圖2 周期提取流程示意
2.1.2 漂移性變化
對于待建模的序列,通常要求它不存在明顯的長期趨勢或是存在全局漂移的現(xiàn)象,否則生成的模型通常無法很好地適應(yīng)指標(biāo)的最新走勢[2]。我們將時間序列隨著時間的變化出現(xiàn)均值的顯著變化或是存在全局突變點的情況,統(tǒng)稱為漂移的場景。為了能夠準(zhǔn)確地捕捉時間序列的最新走勢,我們需要在建模前期判斷歷史數(shù)據(jù)中是否存在漂移的現(xiàn)象。全局漂移和周期性序列均值漂移,如下示例所示:
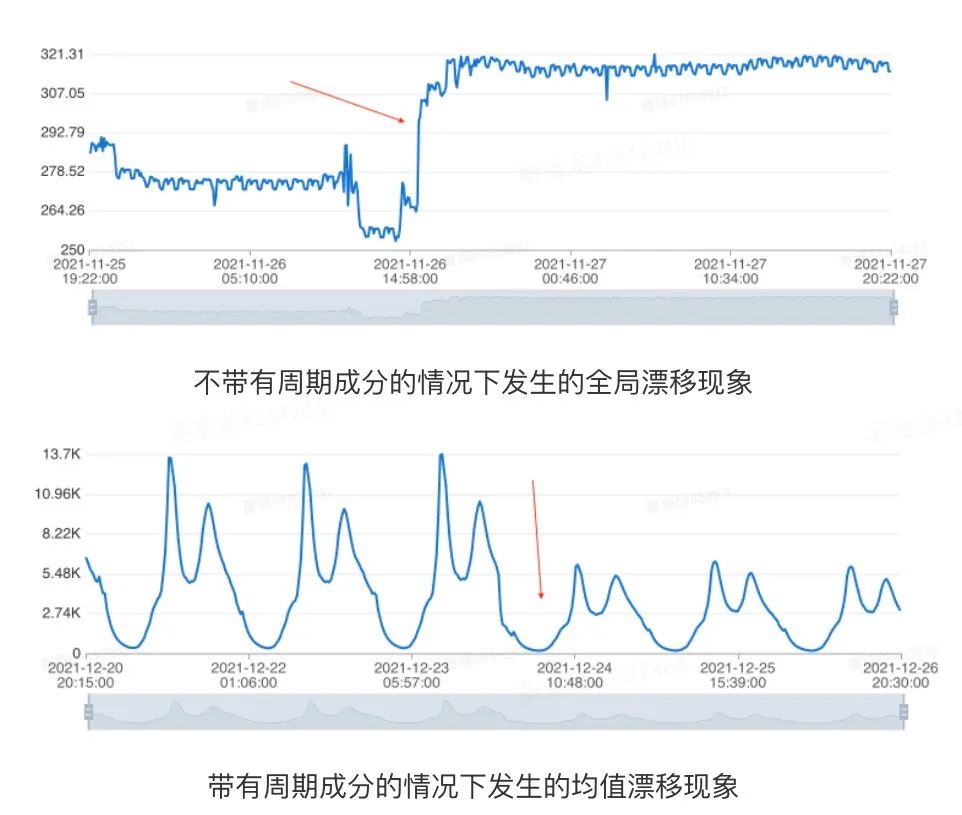
圖3 數(shù)據(jù)漂移示意 數(shù)據(jù)庫指標(biāo)受業(yè)務(wù)活動等復(fù)雜因素影響,很多數(shù)據(jù)會有非周期性的變化,而建模需要容忍這些變化。因此,區(qū)別于經(jīng)典的變點檢測問題,在異常檢測場景下,我們只需要檢測出歷史上很平穩(wěn),之后出現(xiàn)數(shù)據(jù)漂移的情況。綜合算法性能和實際表現(xiàn),我們使用了基于中位數(shù)濾波的漂移檢測方法,主要的流程包含以下幾個環(huán)節(jié): 1. 中位數(shù)平滑
a. 根據(jù)給定窗口的大小,提取窗口內(nèi)的中位數(shù)來獲取時序的趨勢成分。
b. 窗口需要足夠大,以避免周期因素影響,并進行濾波延遲矯正。
c. 使用中位數(shù)而非均值平滑的原因在于為了規(guī)避異常樣本的影響。
2. 判斷平滑序列是否遞增或是遞減 a. 中位數(shù)平滑后的序列數(shù)據(jù),若每個點都大于(小于)前一個點,則序列為遞增(遞減)序列。
b. 如果序列存在嚴(yán)格遞增或是嚴(yán)格遞減的性質(zhì),則指標(biāo)明顯存在長期趨勢,此時可提前終止。
3.遍歷平滑序列,利用如下兩個規(guī)則來判斷是否存在漂移的現(xiàn)象
a. 當(dāng)前樣本點左邊序列的最大值小于當(dāng)前樣本點右邊序列的最小值,則存在突增漂移(上漲趨勢)。
b. 當(dāng)前樣本點左邊序列的最小值大于當(dāng)前樣本點右邊序列的最大值,則存在突降漂移(下跌趨勢)。
2.1.3 平穩(wěn)性變化
對于一個時序指標(biāo),如果其在任意時刻,它的性質(zhì)不隨觀測時間的變化而變化,我們認(rèn)為這條時序是具備平穩(wěn)性的。因此,對于具有長期趨勢成分亦或是周期性成分的時間序列而言,它們都是不平穩(wěn)的。具體示例如下圖所示:
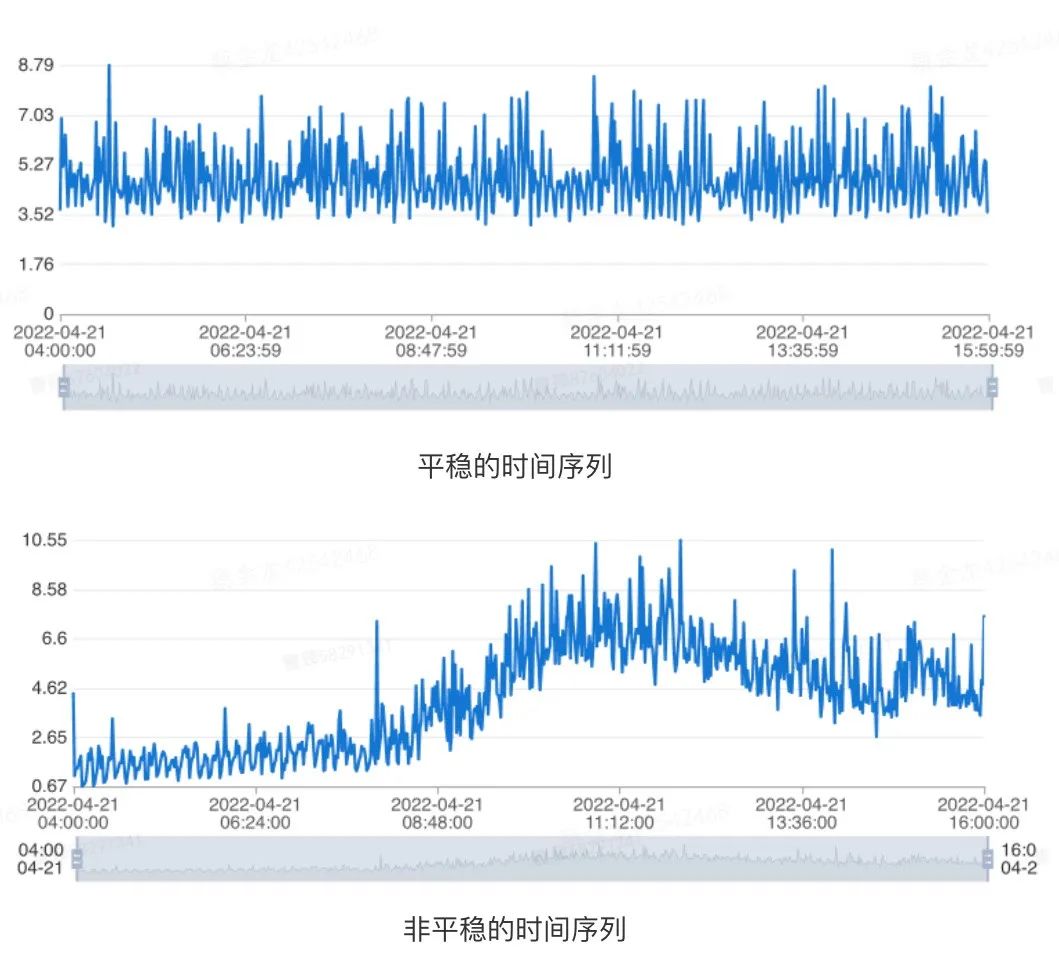
圖4 數(shù)據(jù)平穩(wěn)示意 針對這種情況,我們可以通過單位根檢驗(Augmented Dickey-Fuller Test)[3]來判斷給定的時間序列是否平穩(wěn)。具體地說,對于一條給定時間范圍指標(biāo)的歷史數(shù)據(jù)而言,我們認(rèn)為在同時滿足如下條件的情況下,時序是平穩(wěn)的:
最近1天的時序數(shù)據(jù)通過adfuller檢驗獲得的p值小于0.05。
最近7天的時序數(shù)據(jù)通過adfuller檢驗獲得的p值小于0.05。
3. 算法選型
3.1 分布規(guī)律與算法選擇
通過了解業(yè)界的一些知名公司在時序數(shù)據(jù)異常檢測上公布的產(chǎn)品介紹,加上我們歷史積累的經(jīng)驗,以及對部分線上實際指標(biāo)的抽樣分析,它們的概率密度函數(shù)符合如下情況的分布:
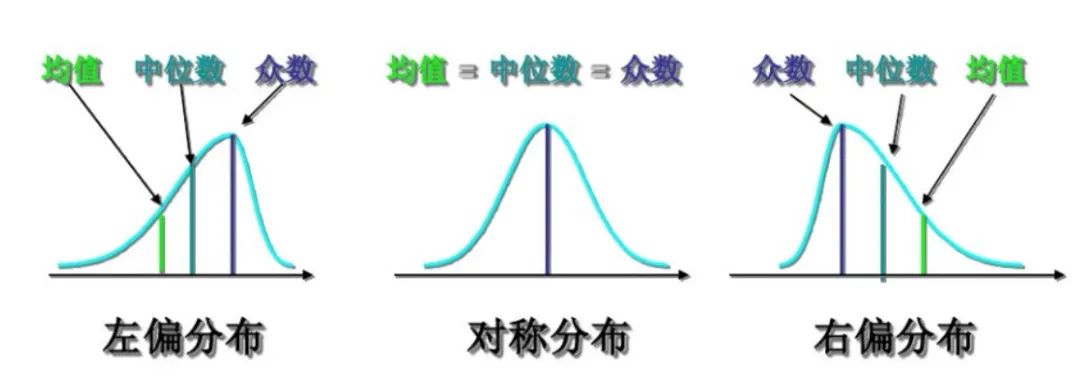
圖5 分布偏斜示意 針對上述的分布,我們調(diào)研了一些常見的算法,并確定了箱形圖、絕對中位差和極值理論作為最終異常檢測算法。以下是對常見時序數(shù)據(jù)檢測的算法對比表:
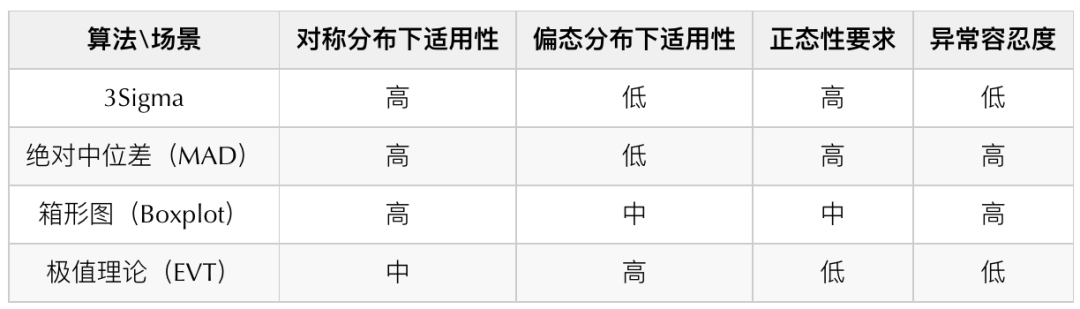
我們沒有選擇3Sigma的主要原因是它對異常容忍度較低,而絕對中位差從理論上而言具有更好的異常容忍度,所以在數(shù)據(jù)呈現(xiàn)高對稱分布時,通過絕對中位差(MAD)替代3Sigma進行檢測。我們對不同數(shù)據(jù)的分布分別采用了不同的檢測算法(關(guān)于不同算法的原理可以參考文末附錄的部分,這里不做過多的闡述):
低偏態(tài)高對稱分布:絕對中位差(MAD)
中等偏態(tài)分布:箱形圖(Boxplot)
高偏態(tài)分布:極值理論(EVT)
有了如上的分析,我們可以得出具體的根據(jù)樣本輸出模型的流程:
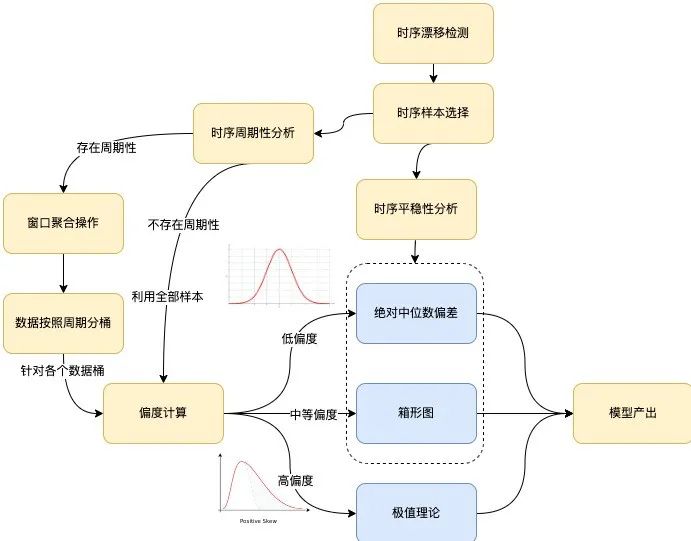
圖6 算法建模流程 算法的整體建模流程如上圖所示,主要涵蓋以下幾個分支環(huán)節(jié):時序漂移檢測、時序平穩(wěn)性分析、時序周期性分析和偏度計算。下面分別進行介紹:
時序漂移檢測。如果檢測存在漂移的場景,則需要根據(jù)檢測獲得的漂移點t來切割輸入時序,使用漂移點后的時序樣本作為后續(xù)建模流程的輸入,記為S={Si},其中i>t。
時序平穩(wěn)性分析。如果輸入時序S滿足平穩(wěn)性檢驗,則直接通過箱形圖(默認(rèn))或是絕對中位差的方式來進行建模。
時序周期性分析。存在周期性的情況下,將周期跨度記為T,將輸入時序S根據(jù)跨度T進行切割,針對各個時間索引j∈{0,1,?,T?1}所組成的數(shù)據(jù)桶進行建模流程。不存在周期性的情況下,針對全部輸入時序S作為數(shù)據(jù)桶進行建模流程。
案例:給定一條時間序列ts={t0,t1,?,tn},假定其存在周期性且周期跨度為T,對于時間索引j而言,其中j∈{0,1,?,T?1},對其建模所需要的樣本點由區(qū)間[tj?kT?m, tj?kT+m]構(gòu)成,其中m為參數(shù),代表窗口大小,k為整數(shù),滿足j?kT?m≥0, j?kT+m≤n。 舉例來說,假設(shè)給定時序自2022/03/01 0000至2022/03/08 0000止,給定窗口大小為5,周期跨度為一天,那么對于時間索引30而言,對其建模所需要的樣本點將來自于如下時間段: [03/01 0000, 03/01 0000]
[03/02 0000, 03/02 0000]
...
[03/07 0000, 03/07 0000]
偏度計算。時序指標(biāo)轉(zhuǎn)化為概率分布圖,計算分布的偏度,若偏度的絕對值超過閾值,則通過極值理論進行建模輸出閾值。若偏度的絕對值小于閾值,則通過箱形圖或是絕對中位差的方式進行建模輸出閾值。
3.2 案例樣本建模
這里選取了一個案例,展示數(shù)據(jù)分析及建模過程,便于更清晰的理解上述過程。其中圖(a)為原始序列,圖(b)為按照天的跨度進行折疊的序列,圖(c)為圖(b)中某時間索引區(qū)間內(nèi)的樣本經(jīng)過放大后的趨勢表現(xiàn),圖(d)中黑色曲線為圖(c)中時間索引所對應(yīng)的下閾值。如下是針對某時序的歷史樣本進行建模的案例:
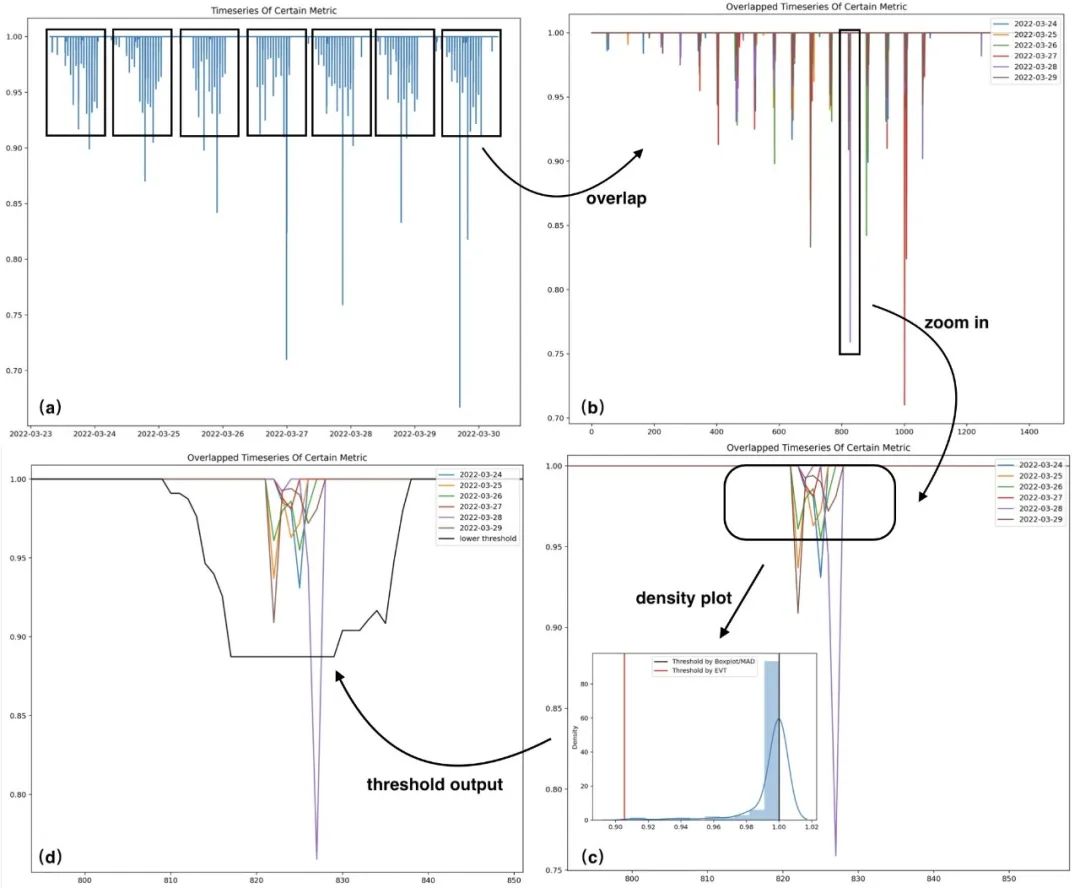
圖7 建模案例 上圖(c)區(qū)域內(nèi)的樣本分布直方圖以及閾值(已剔除其中部分異常樣本),可以看到,在該高偏分布的場景中,EVT算法計算的閾值更為合理。
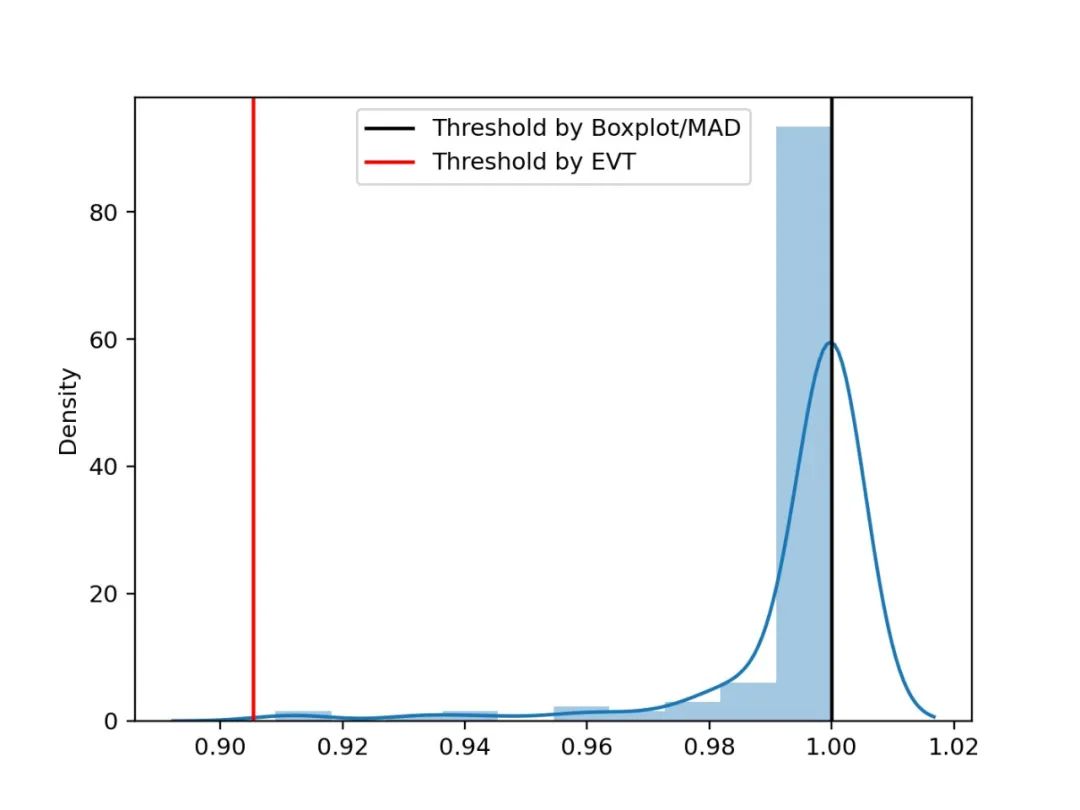
圖8 偏斜分布閾值對比
4. 模型訓(xùn)練與實時檢測
4.1 數(shù)據(jù)流轉(zhuǎn)過程
為了實時檢測規(guī)模龐大的秒級數(shù)據(jù),我們以基于Flink進行實時流處理為出發(fā)點,設(shè)計了如下的技術(shù)方案:
實時檢測部分:基于Flink實時流處理,消費Mafka(美團內(nèi)部的消息隊列組件)消息進行在線檢測,結(jié)果存儲于Elasticsearch(以下簡稱ES)中,并產(chǎn)生異常記錄。
離線訓(xùn)練部分:以Squirrel(美團內(nèi)部的KV數(shù)據(jù)庫)作為任務(wù)隊列,從MOD(美團內(nèi)部運維數(shù)據(jù)倉庫)讀取訓(xùn)練數(shù)據(jù),從配置表讀取參數(shù),訓(xùn)練模型,保存于ES,支持自動和手動觸發(fā)訓(xùn)練,通過定時讀取模型庫的方式,進行模型加載和更新。
以下是具體的離線訓(xùn)練和在線檢測技術(shù)設(shè)計:
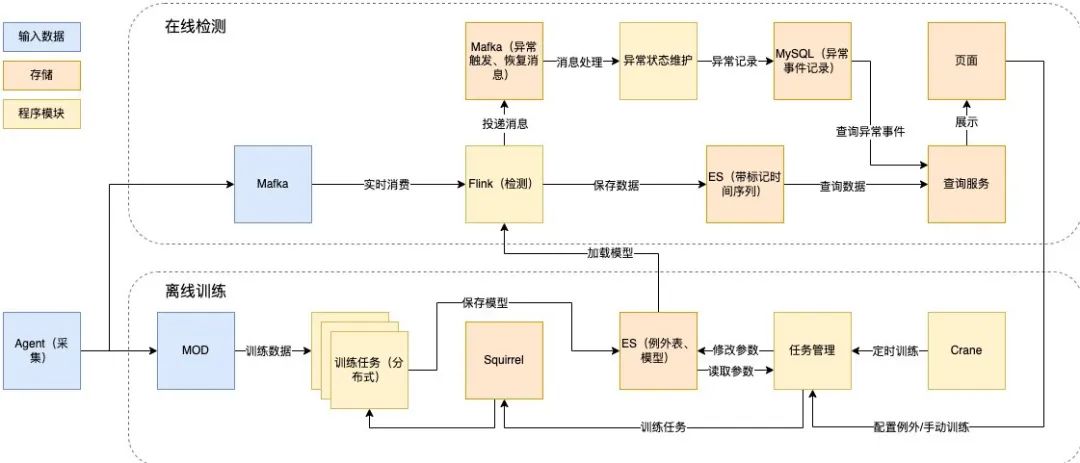
圖9 離線訓(xùn)練和在線檢測技術(shù)設(shè)計
4.2 異常檢測過程
異常檢測算法整體采用分治思想,在模型訓(xùn)練階段,根據(jù)歷史數(shù)據(jù)識別提取特征,選定合適的檢測算法。這里分為離線訓(xùn)練和在線檢測兩部分,離線主要根據(jù)歷史情況進行數(shù)據(jù)預(yù)處理、時序分類和時序建模。在線主要加載運用離線訓(xùn)練的模型進行在線實時異常檢測。具體設(shè)計如下圖所示:
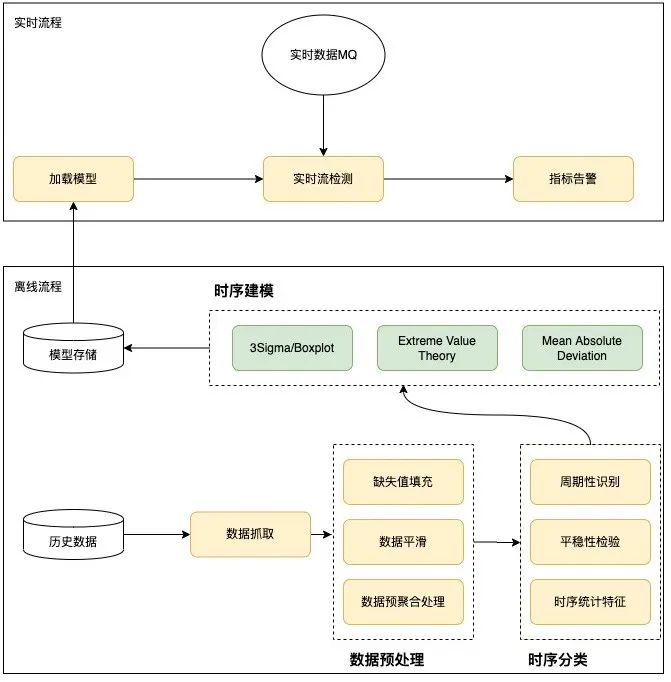
圖10 異常檢測過程
5. 產(chǎn)品運營
為了提高優(yōu)化迭代算法的效率,持續(xù)運營以提高精準(zhǔn)率和召回率,我們借助Horae(美團內(nèi)部可擴展的時序數(shù)據(jù)異常檢測系統(tǒng))的案例回溯能力,實現(xiàn)在線檢測、案例保存、分析優(yōu)化、結(jié)果評估、發(fā)布上線的閉環(huán)。
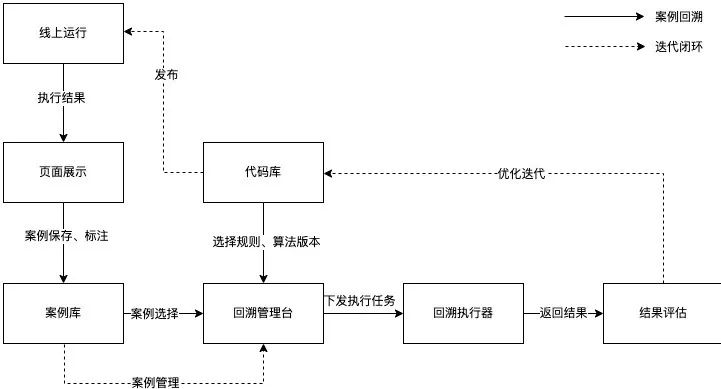
圖11 運營流程
目前,異常檢測算法指標(biāo)如下:
精準(zhǔn)率:隨機選擇一部分檢測出異常的案例,人工校驗其中確實是異常的比例,為81%。
召回率:根據(jù)故障、告警等來源,審查對應(yīng)實例各指標(biāo)異常情況,對照監(jiān)測結(jié)果計算召回率,為82%。
F1-score:精準(zhǔn)率和召回率的調(diào)和平均數(shù),為81%。
6. 未來展望
目前,美團數(shù)據(jù)庫異常監(jiān)測能力已基本構(gòu)建完成,后續(xù)我們將對產(chǎn)品繼續(xù)進行優(yōu)化和拓展,具體方向包括:
具有異常類型識別能力。可以檢測出異常的類型,如均值變化、波動變化、尖刺等,支持按異常類型進行告警訂閱,并作為特征輸入后續(xù)診斷系統(tǒng),完善數(shù)據(jù)庫自治生態(tài)[4]。
構(gòu)建Human-in-Loop環(huán)境。支持根據(jù)反饋標(biāo)注自動學(xué)習(xí),保障模型持續(xù)優(yōu)化[5]。
多種數(shù)據(jù)庫場景的支持。異常檢測能力平臺化以支持更多數(shù)據(jù)庫場景,如DB端到端報錯、節(jié)點網(wǎng)絡(luò)監(jiān)測等。
7. 附錄
7.1 絕對中位差
絕對中位差,即Median Absolute Deviation(MAD),是對單變量數(shù)值型數(shù)據(jù)的樣本偏差的一種魯棒性測量[6],通常由下式計算而得:
其中在先驗為正態(tài)分布的情況下,一般C選擇1.4826,k選擇3。MAD假定樣本中間的50%區(qū)域均為正常樣本,而異常樣本落在兩側(cè)的50%區(qū)域內(nèi)。當(dāng)樣本服從正態(tài)分布的情況下,MAD指標(biāo)相較于標(biāo)準(zhǔn)差更能適應(yīng)數(shù)據(jù)集中的異常值。對于標(biāo)準(zhǔn)差,使用的是數(shù)據(jù)到均值的距離平方,較大的偏差權(quán)重較大,異常值對結(jié)果影響不能忽視,而對MAD而言少量的異常值不會影響實驗的結(jié)果,MAD算法對于數(shù)據(jù)的正態(tài)性有較高要求。
7.2 箱形圖
箱形圖主要通過幾個統(tǒng)計量來描述樣本分布的離散程度以及對稱性,包括:
Q0:最小值(Minimum)
Q1:下四分位數(shù)(Lower Quartile)
Q2:中位數(shù)(Median)
Q3:上四分位數(shù)(Upper Quartile)
Q4:最大值(Maximum)
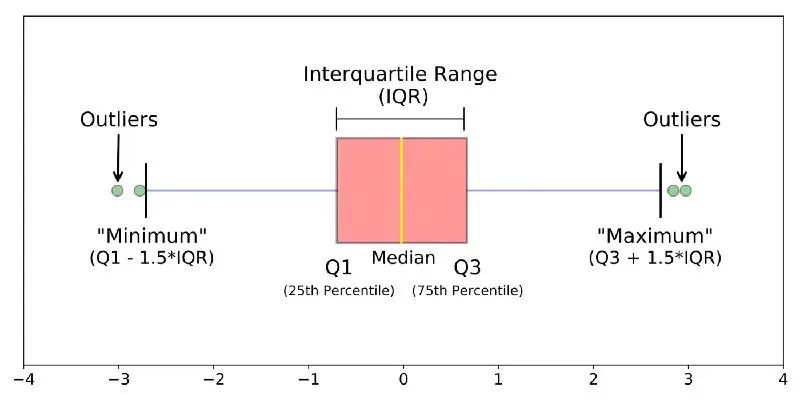
圖12 箱線圖
將Q1與Q3之間的間距稱為IQR,當(dāng)樣本偏離上四分位1.5倍的IQR(或是偏離下四分位數(shù)1.5倍的IQR)的情況下,將樣本視為是一個離群點。不同于基于正態(tài)假設(shè)的三倍標(biāo)準(zhǔn)差,通常情況下,箱形圖對于樣本的潛在數(shù)據(jù)分布沒有任何假定,能夠描述出樣本的離散情況,且對樣本中包含的潛在異常樣本有較高的容忍度。對于有偏數(shù)據(jù),Boxplot進行校準(zhǔn)后建模更加符合數(shù)據(jù)分布[7]。
7.3 極值理論
真實世界的數(shù)據(jù)很難用一種已知的分布來概括,例如對于某些極端事件(異常),概率模型(例如高斯分布)往往會給出其概率為0。極值理論[8]是在不基于原始數(shù)據(jù)的任何分布假設(shè)下,通過推斷我們可能會觀察到的極端事件的分布,這就是極值分布(EVD)。其數(shù)學(xué)表達(dá)式如下(互補累積分布函數(shù)公式):其中t代表樣本的經(jīng)驗閾值,對于不同場景可以設(shè)置不同取值,,分別是廣義帕累托分布中的形狀參數(shù)與尺度參數(shù),在給定樣本超過人為設(shè)定的經(jīng)驗閾值t的情況下,隨機變量X-t是服從廣義帕累托分布的。通過極大似然估計方法我們可以計算獲得參數(shù)估計值與 ,并且通過如下公式來求取模型閾值: 上述公式中q代表風(fēng)險參數(shù),n是所有樣本數(shù)量,Nt是滿足x-t>0的樣本數(shù)量。由于通常情況下對于經(jīng)驗閾值t的估計沒有先驗的信息,因此可以使用樣本經(jīng)驗分位數(shù)來替代數(shù)值t,這里經(jīng)驗分位數(shù)的取值可以根據(jù)實際情況來選擇。
審核編輯:湯梓紅
-
算法
+關(guān)注
關(guān)注
23文章
4601瀏覽量
92671 -
AI
+關(guān)注
關(guān)注
87文章
30239瀏覽量
268474 -
數(shù)據(jù)庫
+關(guān)注
關(guān)注
7文章
3767瀏覽量
64279
原文標(biāo)題:基于AI算法的數(shù)據(jù)庫異常監(jiān)測系統(tǒng)的設(shè)計與實現(xiàn)
文章出處:【微信號:OSC開源社區(qū),微信公眾號:OSC開源社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
CE6.0內(nèi)置數(shù)據(jù)庫CEDB的異常檢測與修復(fù)
大型網(wǎng)絡(luò)異常數(shù)據(jù)庫的快速數(shù)據(jù)定位模型仿真
OpenStack數(shù)據(jù)庫服務(wù)與Trove的介紹
基于樹結(jié)構(gòu)的回溯異常檢測算法
數(shù)據(jù)庫引擎是什么

面向NoSQL數(shù)據(jù)庫的JSON文檔異常檢測模型
基于PCA和隨機樹的數(shù)據(jù)庫異常訪問檢測算法
云數(shù)據(jù)庫和服務(wù)器數(shù)據(jù)庫的區(qū)別是什么,哪個比較好
AlloyDB數(shù)據(jù)庫云服務(wù)的優(yōu)勢
MySQL數(shù)據(jù)庫服務(wù)器、數(shù)據(jù)庫和表之間是什么關(guān)系
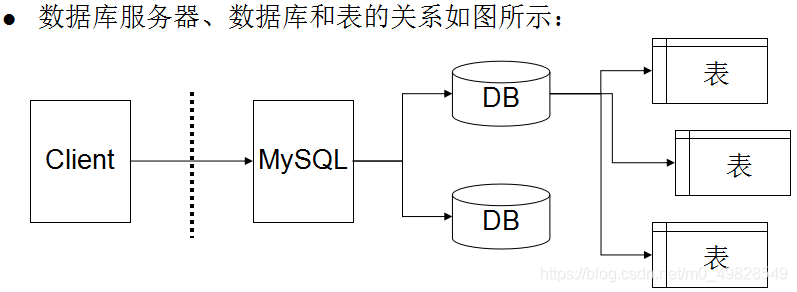
服務(wù)器怎么用數(shù)據(jù)庫建設(shè)網(wǎng)站
云數(shù)據(jù)庫和普通數(shù)據(jù)庫區(qū)別?|PetaExpress云端數(shù)據(jù)庫
oracle數(shù)據(jù)庫alert日志作用
oracle數(shù)據(jù)恢復(fù)—服務(wù)器斷電導(dǎo)致Oracle數(shù)據(jù)庫異常的數(shù)據(jù)恢復(fù)案例
Oracle數(shù)據(jù)恢復(fù)—異常斷電后Oracle數(shù)據(jù)庫啟庫報錯的數(shù)據(jù)恢復(fù)案例




 基于AI算法的數(shù)據(jù)庫異常檢測服務(wù)
基于AI算法的數(shù)據(jù)庫異常檢測服務(wù)










評論