一. 前言
到目前為止,我的雙目立體匹配系列文章已經完成了接近經典視差優化算法的介紹,讓我們觀察一下現在的進度:
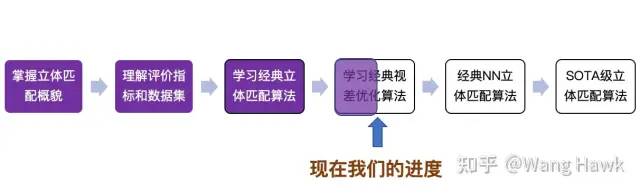
今天的文章,我們先從回顧立體匹配的評價指標開始,MiddleBurry立體匹配排行榜的評價指標:
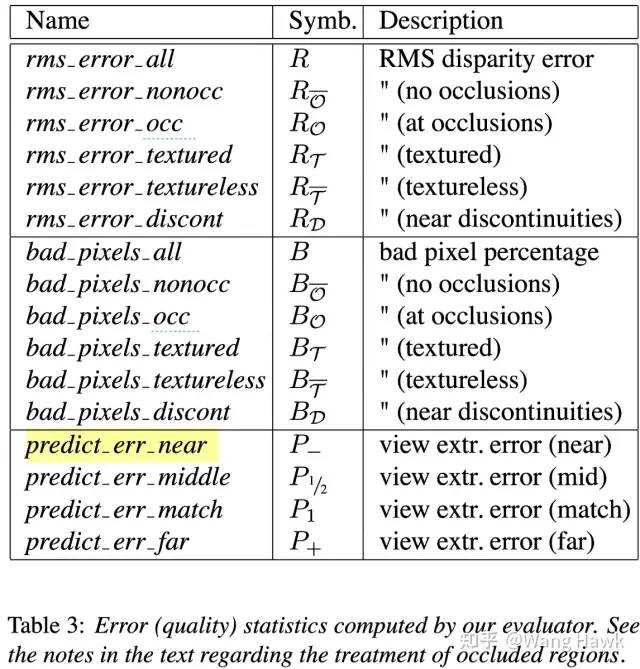
MiddleBurry立體匹配評價指標 這些評價指標大概包括:
在全圖上計算視差圖和理想視差圖之間的均方根誤差,及錯誤像素占比
在無紋理區域,有紋理區域,遮擋區域,非遮擋區域,深度不連續區域共5個區域計算和理想視差圖之間的均方根誤差,及錯誤像素占比
在不同視角下進行反向變換,計算變換后的投影誤差,即所謂預測誤差
在我介紹其他的數據集里,基本上采用了類似的評價指標。我不知道你想過沒有,這些評價指標有什么特點? 事實上,這些指標都在強調視差圖在視差方向上的準確性,卻沒有怎么強調視差圖與原圖之間的貼合性——或者說,它們都在強調Z方向的準確性,卻沒有重視其在X/Y方向上的準確性。 對于很多三維重建的應用,比如測距、尺寸測量、甚至自動駕駛中的障礙物檢測識別,似乎這也沒有構成很大的問題。然而有一類應用,對重建后的深度或視差在X/Y方向上的準確性確有很高很高的要求,虛化渲染類應用——事實上我認為絕大多數像素級渲染類的應用,都對場景模型和圖像紋理之間的貼合度有很高的要求,而這也意味著我們要求深度圖中的內容和原始的彩色圖之間也需要緊密貼合。

虛化渲染對邊緣貼合有很高要求 如果不能做到這點,我們渲染的結果就會出現非常突兀的瑕疵,比如下面這樣的:

邊緣不貼合出錯 或是這樣的:

邊緣不貼合出錯 很顯然,一般的基于MiddleBurry類數據集評價指標開發的立體匹配算法是無法滿足這種需求的。我們所需要的算法,必須要從原理上能夠保證這種貼邊,今天我將要展示的算法就做到了這一點。按照作者的說法,根據這種算法的原理你甚至無法生成不貼邊的視差圖! 在正式介紹今天的算法之前,讓我們先來看看效果。首先我們來看看一對輸入的經過立體校正的圖像,及其局部(下方):

然后我們看看普通的SGM算法得到的視差圖,以及用這種視差圖進行淺景深虛化渲染的結果。你可以很清楚的看到細節部分出現了嚴重的不貼邊現象:

SGM算法結果和渲染圖 下面則是我今天將要介紹的算法的結果。真是不怕不識貨,就怕貨比貨啊,從渲染的結果看上去明顯好了很多!

本文算法結果和渲染圖 下面是另外一個場景,注意看原圖中雕塑的細節部分。由于上采樣看細節的緣故,小圖顯得不那么清晰,可以忽略這一點。

輸入原始圖 我們先看看一個叫做SPS-StFI的算法結果:

SPS-StFI算法渲染結果 表面上看起來視差圖還OK,但我們看看渲染的細節,很明顯在雕塑的邊緣處出現了奇怪的瑕疵,你可以和上面的原圖對比一下,這顯然是由于視差圖中的邊緣錯誤導致的

SPS-StFI算法渲染結果細節 現在來看看本文將要介紹的算法的結果:

本文算法結果 看細節,很明顯主體和虛化背景的邊界非常自然,沒有出現上面SPS-StFI算法的邊緣瑕疵:

本文算法渲染細節 小結一下我們現在得到的信息: 傳統的基于類似MiddleBurry這樣的數據集的評價指標來設計的雙目立體匹配算法,大多數側重于視差值或者深度值的準確性,卻對視差圖貼合原圖物體邊緣的程度不夠重視,不適合圖形圖像渲染類應用。而有一類算法,比如說我今天將要介紹這種算法,特別強調視差圖與原圖目標邊緣的貼合程度,從而比較適合產生渲染類應用所需要的視差圖(深度圖)。 那么是什么樣的算法能夠從原理上保證這一點呢?它是如何做到的呢?讓我請出今天的主角吧:

對,就是Jon Barron,有的朋友可能已經知道他了。如果我再提及他參與提出的NeRF(神經輻射場),就肯定有更多人會哇哦了。 我們今天要談的是Jon Barron在2015年CVPR上演講展示的一篇文章Fast Bilateral-Space Stereo for Synthetic Defocus

它首先從原理上保證了視差圖的貼邊,而且速度還大大超越其他算法,在下圖中我們看到它比之前最快的算法還快十幾倍!
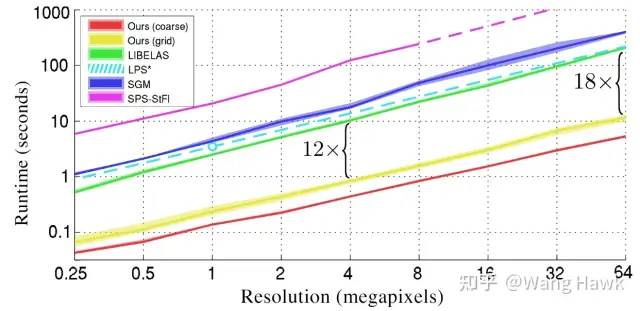
本文算法速度非常快 那么,它是如何做到的呢?要回答這個問題,我們需要先回顧一下立體匹配的全局優化法的思想。
二. 全局優化算法的思想
在我的文章72. 三維重建7-立體匹配3,立體匹配算法中的視差優化中,我曾經講過,立體匹配的全局代價優化法的思想是希望尋找到每個像素的最優視差結果,使得全局的、整體的匹配代價最小,這一步被稱為視差優化(Disparity Optimization)。于是這個過程就變成了一個最優化某個能量函數的過程,該函數通常寫成如下的形式:
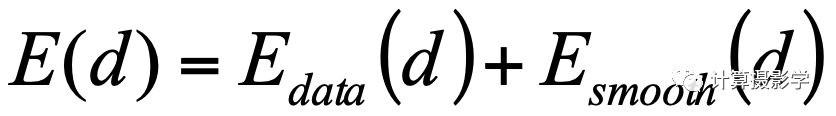
等號右邊第1項是數據項,它衡量計算出的視差與實際輸入圖像關系的差異。一般來說,可以用下面的式子來表示,其中C表示代價函數。
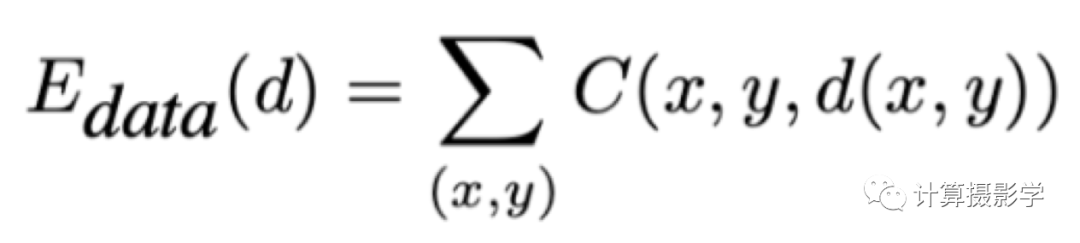
這一項用于約束全局代價最小化。但是代價函數中通常含有噪聲和錯誤,直接最小化求得的結果也會有很多問題,所以還需要第2項平滑項。這一項一般用于給出某些額外的約束條件,比如通常假設整個圖像的視差是平滑變化的。這樣視差的大變化只會在場景內視差邊緣處產生,一般也和圖像內物體邊緣高度相關。 很顯然,這個全局代價的優化是非常困難和復雜的問題。比如,一幅1024x1024的圖像,如果其有效視差范圍為128,那么上面的數據項就是一個有著1024x1024x128=134217728個元素的巨大的立方體。這還沒有算上后面的平滑項的復雜度。 其實,雖然如此復雜,但似乎也不是不可以接受,無非就是多花些時間吧。然而,在有些應用場景下,我們需要高速進行深度重建,甚至實時深度重建,比如我提到的手機上的各種渲染應用就是如此。你想象一下,你拿起手機要給女朋友/男朋友拍一張人像照,肯定是希望所見即所得,并且按下快門立馬得到結果,而不是等上幾分鐘都看不到效果吧。 所以,總結下Jon Barron要想解決的問題:用極高的速度解決立體匹配的全局代價優化問題 在計算機科學中,甚至在所有門類的科學中,有一種思想是問題的轉換。我們不是說上面的全局代價函數的規模太大,導致優化復雜嗎?那么,就先把這種大規模的全局代價函數轉換成小規模的全局代價函數吧,這樣求解起來不就簡單了嗎?
我們接著來看看Jon是如何一步步做到這種轉換的。
三. 視差圖的平滑性與雙邊濾波
現在重新想想我們的視差圖需要滿足什么樣的特性:視差圖總體上是平滑變化的,視差的突然變化只會在場景內物體的邊緣處產生。你想到什么了嗎?這和什么算法有相通之處? 是的,這和我之前講過的雙邊濾波有非常大的相似之處,讓我們回憶下4. 數碼相機內的圖像處理-更多圖像濾波中的內容: 高斯濾波只使用了空間距離來衡量像素的權重,而雙邊濾波則在空間距離的基礎上,加入了像素亮度距離。而由于邊緣兩邊的亮度值差異很大,因此越過邊緣的像素的濾波權重很小,這就是雙邊濾波能夠保持邊緣的秘訣。 雙邊濾波的圖示如下:
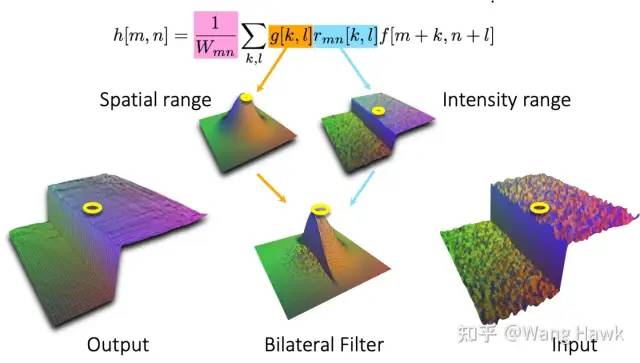
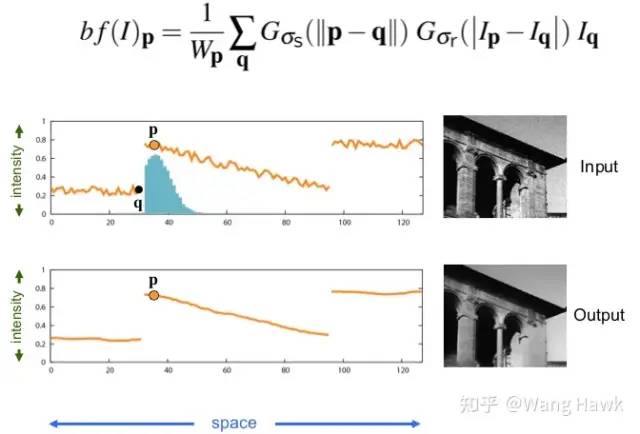
雙邊濾波有這種優異的性質,但其計算量卻非常大,這也促使了人們想了各種各樣的辦法來快速計算雙邊濾波。其中有一種稱為雙邊網格的方法特別有意思,這是2007年Chen Jiawen等人提出的。

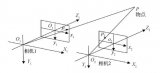
我們看下面的圖,這就是Bilateral Grid(雙邊網格)的思想。一幅2D的灰度圖像中的每個像素,按照其x坐標、y坐標、灰度值,被分組放到了一個3D的立方體中,每一小組就是一個格子。這樣,原本在2D空間中相鄰的像素,到了雙邊網格空間中,就不相鄰了,至少被放到了不同的格子里。
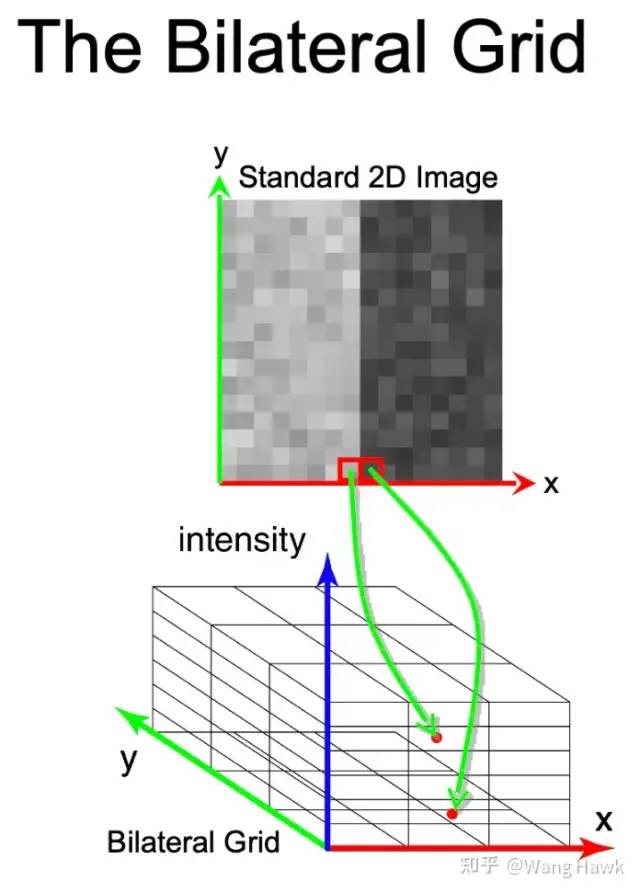
利用這種思想,我們實際上是對原始圖像進行了降維,并且使得灰度值差異較大的像素不會相互污染:
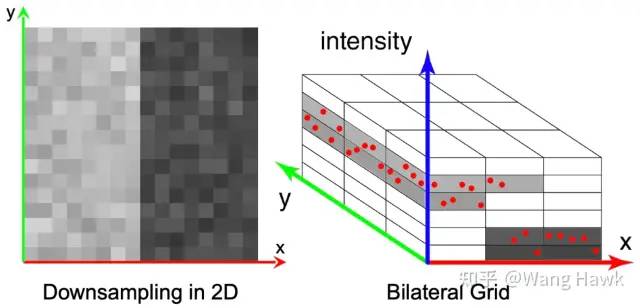
利用這種思想,可以實現快速的雙邊濾波,我們以一個一維圖像來舉例。首先,我們用剛才的思想把圖像投射到 雙邊網格中。接下來,我們在雙邊網格空間中進行高斯濾波。最后再把濾波后的雙邊網格重新投射回原始的圖像,如下圖所示:
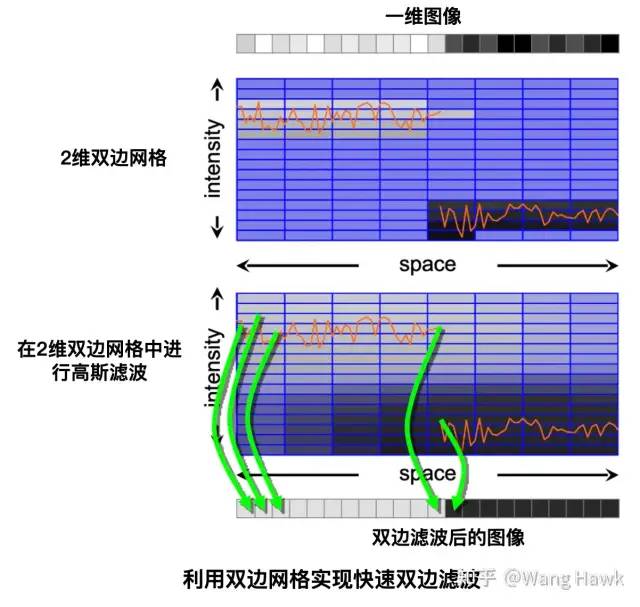
由于雙邊網格的規模大大小于原始圖像,比如一幅八百萬像素的圖像投射到雙邊網格中可能只有70*70*10=49000個格子。而高斯濾波又比雙邊濾波的計算量低很多,并且很容易通過GPU來并行計算。因此通過這樣的方式,就可以實現非常快速的雙邊濾波了。 比如Chen JiaWen等在演講中提到,一幅兩百萬像素的圖像,如果用原始的CPU上實現的雙邊濾波需要10分鐘,而用他們的雙邊網格思想在2006年的G80 GPU上實現,只需要9毫秒!這就是將難解問題轉換成易解問題的威力,讓我們再看一遍這個圖,即便你研究的領域并非立體匹配,并非圖像濾波,今天這篇文章的其他內容你都可以忘記,但我希望你記住這幅圖:

在相關文獻中,把從原始圖像到雙邊空間的過程稱為Splat,在雙邊空間中進行濾波稱為Blur,把濾波后的結果轉換到原始圖像像素空間中的過程稱為Slice。Splat-Blur-Slice,就是這類方法的三個重要步驟。由于高斯濾波是可以分解的,在雙邊網格中的高斯濾波可以變換為每個維度上(對于1維圖像來說是space和intensity兩個維度)分別進行的一維濾波相加的結果(這是一種近似)
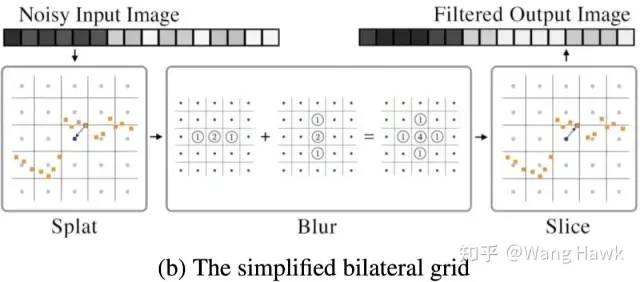
那么,這對我們今天講的立體匹配全局代價函數優化有什么啟示呢? Jon Barron在演講材料中寫道:

什么意思?前人的工作是將圖像信號投射(Splat)到雙邊空間,在雙邊空間中濾波(Blur),再反投射(Slice)濾波后的圖像信號到原始像素空間。而Jon Barron的工作則是將所要求解的最小化問題投射(Splat)到雙邊空間,在雙邊空間中求解(Solve)該問題,再將求解結果重新投射(Slice)到原始空間。 由于雙邊空間中的問題規模大大小于原始問題,因此問題求解就變得很快速很容易了。我們在下一節,進一步看看Jon是如何做到的。
四. 利用雙邊空間優化全局代價函數
我們看看下面Jon構建的代價函數,加號前面一項是平滑項,后面一項是數據項,我們就是要最小化這個式子,
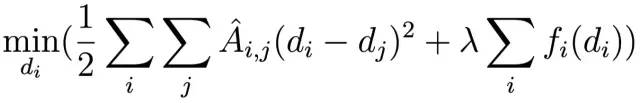
全局匹配代價函數
4.1 平滑項
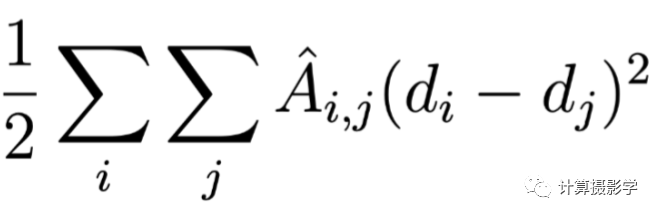
平滑項 平滑項中的di和dj是一幅視差圖中不同位置的像素的視差值。這個時候,我們要把視差圖看作展開的一維向量。一個寬高分別為W和H的視差圖,展開后就是WHx1的一維向量,于是i和j就是不同像素的編號,或者坐標值。 最神秘的是這里的矩陣,為了理解它,我們首先得重新回到雙邊濾波器的矩陣表達,如果x是一個一維表示的尺寸為WHx1的圖像,我們可以用下面的公式來表示雙邊濾波,等號坐標是濾波后的圖像y,尺寸還是WHx1:
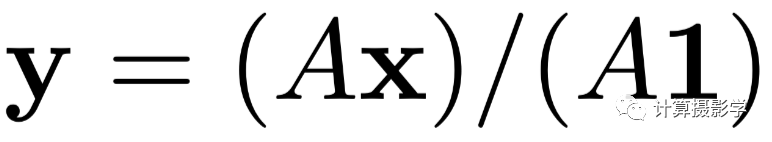
雙邊濾波矩陣表示法 這里的矩陣A是一個對稱的矩陣,尺寸是WHxWH。對于彩色圖像的雙邊濾波,A矩陣的每個元素如下:
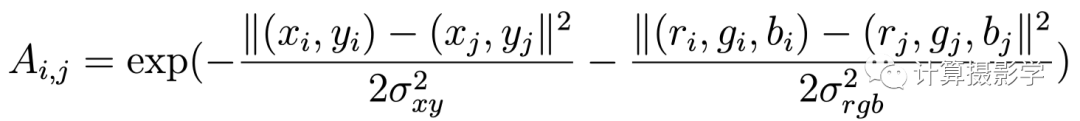
雙邊濾波權重 它實際上是表示第j個像素和第i個像素間的在空間和顏色上的相似度。如果兩個像素越靠近,并且顏色越相似,其對應的A元素就越大,當然如果是單色圖像那么就只是計算空間和亮度上的相似度。 我們看看下面這個3x3的小圖像(我們假設其中存儲的就是對應像素的視差)

3x3的小圖像 按照上面的公式很容易計算得到其雙邊濾波矩陣如下
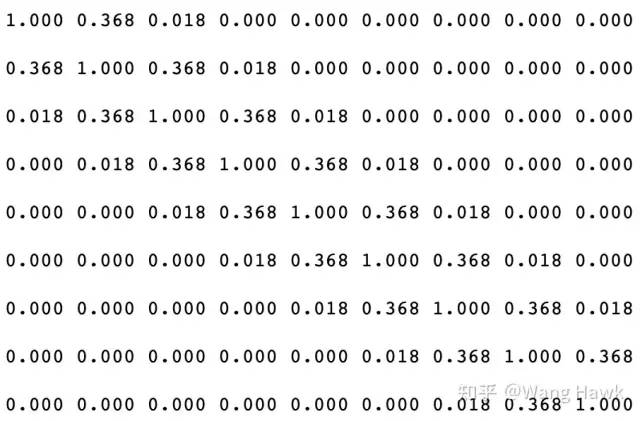
權重矩陣A示意 利用這個矩陣,可以把任何我們認為相鄰的像素的視差值加權平均到一起,得到最后的濾波結果。而我們前面數據項中的矩陣則是雙邊濾波矩陣A的某種特殊歸一化形式,其最大特點是每一行和每一列的和都為1。 4.2 平滑項轉換到雙邊網格空間 我們可以用下面的公式表示雙邊網格算法,其中S矩陣代表我最開始提到的Splat操作,將像素值投射到雙邊空間。B矩陣代表雙邊空間中進行的模糊操作,而ST矩陣則代表上面提到的Slice操作,將雙邊空間中的濾波結果重新投射到原始像素空間。在雙邊網格的構造過程中,每個網格的頂點采用了最近鄰方式采樣,所以這種方式是對原始雙邊濾波的一種近似:
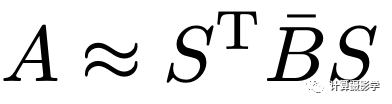
雙邊網格是矩陣分解過程 進行變量替換后,雙邊濾波就變成了下面這樣:
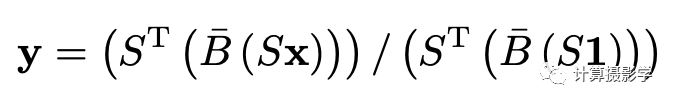
在雙邊空間中進行濾波 而作者最精妙的一點是,把匹配代價中的平滑項按照類似的方法,投射到了雙邊空間。為了做到這一點,首先是把原始的平滑項寫成矩陣表達形式, 再通過變量替換轉換到雙邊空間

下面對雙邊網格中的各個變量作出解釋,請注意在雙邊空間中的這些矩陣和向量的規模都是大大低于像素空間中的對應實體的,這也為之后的快速求解打下了基礎。
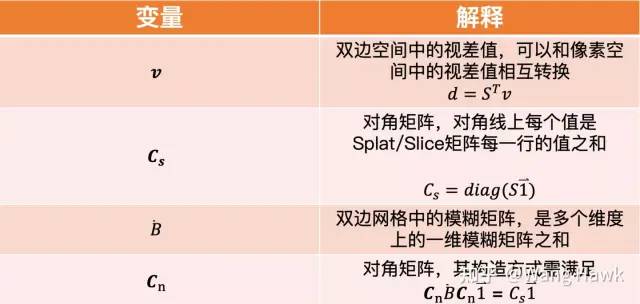
你可能對為什么Jon Barron能夠把原始像素空間中的平滑項做上面所說的轉換感興趣。這里面有非常復雜的數學推導過程,都記錄在了其論文的附加材料里面。不過很多人直接閱讀此份附加材料也是看不懂的(也許你就在這些人里面 )。如果你對此感興趣的話,可以私聊我。如果咨詢的人足夠多,我還打算在我的知識星球中做更詳細的講解,包括針對代價做細致的分析。
4.2 數據項
現在我們來看看數據項。正如前面所說,數據項表示的是像素點的匹配代價
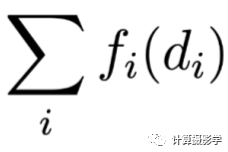
數據項 我們把它也要投射到雙邊空間中——每個雙邊網格所對應的代價值是多個原始像素代價值的加權平均:
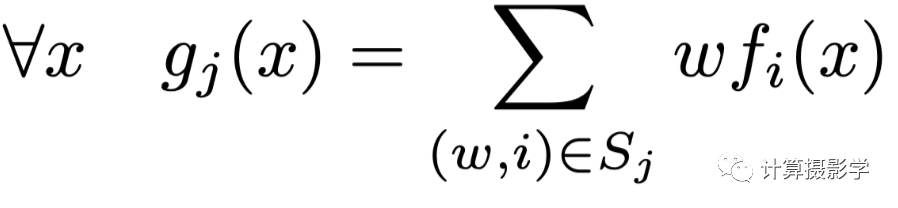
編號為j的網格對應的匹配代價 比如,這里j代表第j個雙邊網格中的格子,其中包含了多個以下標i表示的原始像素,w代表像素的權重。這樣就把像素空間中的代價fi轉換成了雙邊空間中的代價gj 現在我們匯總一下,原始的代價函數為:
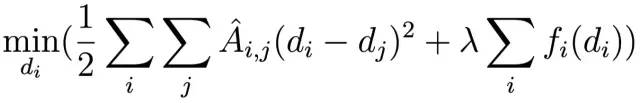
像素空間全局代價函數 在雙邊空間中的代價函數為:
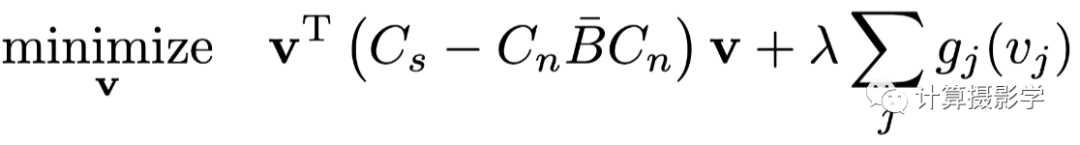
雙邊空間全局代價函數 為了讓計算盡可能簡單,而且可優化,這就需要g是一個連續函數,且可導,這也意味著f是一個連續可導的函數,現在我們必須寫出g函數。 我在之前的文章中介紹過了很多種不同的匹配代價函數,而作者選擇的是下面這個滿足所謂Birchfield-Tomasi 標準的函數:
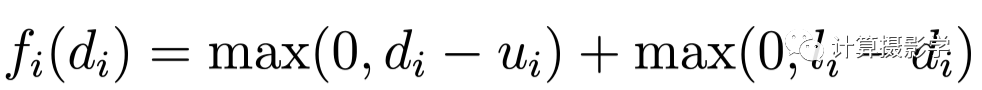
我先在下面給出作者論文中的圖示,然后用人話給你解釋一下:
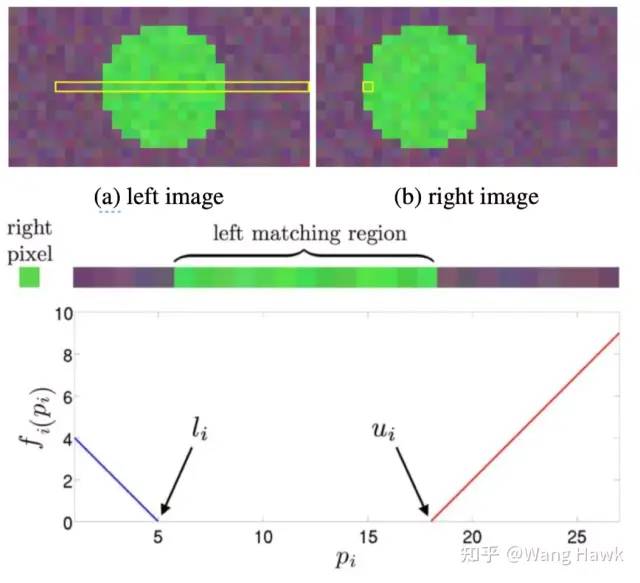
單像素匹配代價示意 什么意思?如果兩個像素通過某種標準判斷是匹配的,那么其匹配代價為0. 否則,其匹配代價正比于代價值偏離匹配范圍的大小。對任何一個像素i,在水平極線上都有可能有多個匹配的像素。其第1個匹配的像素對應的視差我們稱為li, 最后一個匹配的像素對應的視差值我們稱為ui。所以只要di在[li,ui]之間,我們認為是匹配的,代價為0,否則匹配代價將位于斜率為1或-1的直線上。在實際操作中,我們需要記錄每個像素的匹配視差的上下值,其過程我這里略過,感興趣的私聊我吧。 相比我之前介紹的很多匹配代價函數,這是一種很弱的匹配代價函數。作者選擇它并非因為它有什么神奇的地方,僅僅是因為它非常高效,特別是當我們需要最小化之前提到的全局代價函數時這一點尤為重要。
4.3 在雙邊空間中進行優化
希望你還沒有暈掉 我們已經得到了雙邊空間中的數據項和平滑項了,為了進行優化我們需要將數據項表示為連續可導的函數。所以這里采用了線性插值的方法,將在雙邊空間中離散的g函數變為連續的,原論文公式如下:
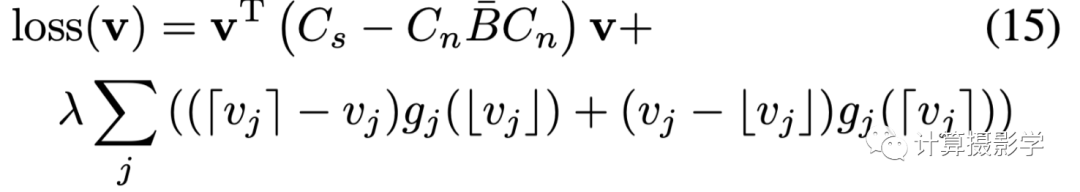
雙邊空間中的全局代價函數 最優化問題有很多求解方法,作者采用的是一種叫做L-BFGS的方法,這是一種在有限的內存空間中進行的優化算法,是Broyden,Fletcher,Goldfarb,Shanno這幾位數學家發明的,他們名字的首字母組合就是BFGS

BFGS 我們不需要了解算法的細節,只需要記住許多最優化問題求解的一般流程如下:

優化算法過程 所以我們再把上述代價函數的梯度表達出來,原論文的梯度公式如下
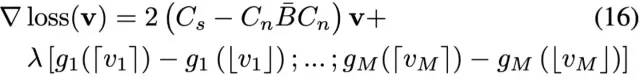
有了上面的(15)和(16)兩個式子,我們就可以進行優化求解了。首先用下面的(17)式,我們求解雙邊空間中的視差值v*,然后把v*重新投射到像素空間中,得到最終的視差值
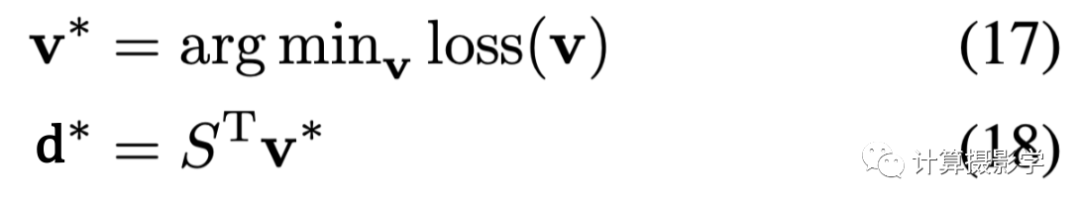
Solve/Splice
五. 實驗和討論
我已經在文章開頭展示了作者演示的效果,我總體上的感覺是這種算法在當目標和背景的顏色不一致時,視差邊緣很貼合目標的邊緣,我將作者給出的視差圖和原始彩色圖疊到一起給你看看,很明顯能看出來。

不過,由于作者采用的數據項中匹配代價函數過于簡單,這也就使得數據項誤差較大,導致算法會出現過平滑的現象。表現在結果上,就是會在結果視差圖中帶入很多原圖的紋理。我們來看幾張網上的高人實現算法后跑出的結果(參考資料4):


六. 總結
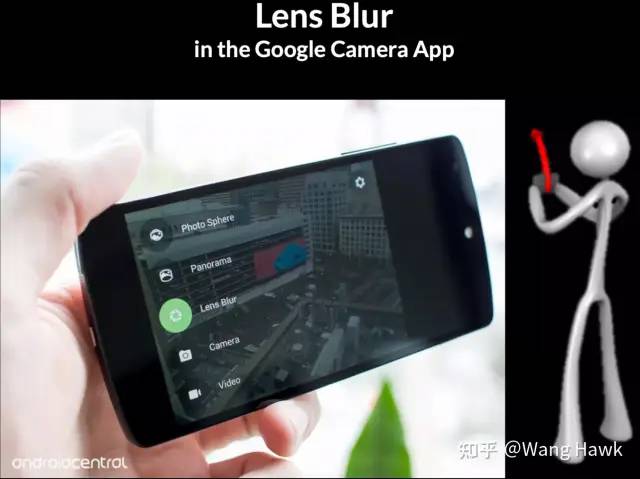
今天我們學習的這種叫做Fast Bilateral-Space Stereo的算法與之前介紹的其他立體匹配算法有很大的不同。它并不追求深度重建結果在Z方向的絕對精確,反而更強調其在X/Y方向的貼邊。因此其結果更適合在圖形圖像渲染領域中使用,而非在對尺寸、距離等有嚴格要求的三維重建領域。該算法速度很快,因此一經推出,就在Google的Camera應用中得到了應用,該功能被稱為Lens Blur,專用于淺景深虛化,也就是現在大家熟悉的手機上的人像虛化模式。
我們從作者的思路中學到的最關鍵的洞見是:一個復雜大規模的問題可以通過空間轉換,變換為小規模的問題。求解完小規模的問題后,再重新映射回原始的問題空間,得到想要的解。

實際上,關于這篇文章還有很多可以講的,但限于篇幅原因我不得不略過了。但有兩大內容,我非常建議讀者進一步學習:
雙邊網格的原理和具體實現方法,這是本文的基礎,也是我接下來還會描述的另外一個算法的基礎。而且快速雙邊濾波在很多領域都有用,因此我覺得掌握雙邊網格很有用。
本文所略過的Jon Barron的匹配代價平滑項、數據項轉換到雙邊空間的具體推導過程。這是本算法背后的精髓所在,理解了它對理解我下一篇文章也很有幫助。
上面兩點,我都會給出公開的參考資料。但坦率說,這些論文和公式你不就是不愿意自己讀嘛所以,如果你真的感興趣,可以加入我創建的知識星球咨詢,咱們通過付費學習的方式把這些重要的問題搞懂,豈不甚好O(∩_∩)O 現在來看看咱們在雙目立體匹配上的學習進度:
你可能會想,怎么視差優化算法還沒有完?是的,因為我們下一次將學習Jon Barron等在2016年ECCV上發表的算法The Fast Bilateral Solver,簡稱FBS,它是The Fast Bilateral-Space Stereo算法的自然衍生,但里面的數學知識和優化方法都有了很多擴展,得到的效果也很不錯。而且,除了立體匹配,還能用于包括圖像分割、畫筆繪制等在內的很多計算機視覺問題。讓我們拭目以待吧 下面是我的文章涉及的領域

這是我最近正在創作攝影圖像后期處理和優化課程的部分內容提綱:
七. 參考資料
1、Jon Barron主頁:jonbarron.info/ 2、原始論文:Fast Bilateral-Space Stereo for Synthetic Defocus 作者的附加材料,給出了推導過程,很難懂 3、很好的一份國外大神的解讀:Ugo Capeto. On fast bilateral-space stereo for synthetic defocus bybarron et al. dropbox.com/s/ke46mg8pk stereo.pdf?dl=0. Accessed September 28, 2016. 4、雙邊網格的論文:Jiawen Chen, Sylvain Paris, and Frédo Durand. Real-time edge-aware image processing with the bilateral grid. In ACM Transactions on Graphics (TOG), volume 26, page 103. ACM, 2007 5、三維重建9-立體匹配5,解析MiddleBurry立體匹配數據集
審核編輯 :李倩
-
算法
+關注
關注
23文章
4599瀏覽量
92645 -
圖像
+關注
關注
2文章
1083瀏覽量
40418 -
數據集
+關注
關注
4文章
1205瀏覽量
24644
原文標題:雙目視覺經典視差優化算法:Fast Bilateral-Space Stereo
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何制定一套優質的工業視覺檢測算法方案?

神經網絡優化算法有哪些
機器學習的經典算法與應用

計算機視覺的十大算法

視覺、激光、結構光?掃地機器人導航避障技術盤點
基于IMX214+ZYNQ XC7Z100的1080P雙目視覺智能平臺
三維視覺測量技術:被動視覺測量和主動視覺測量
【技術干貨】PID算法原理分析及優化
LabVIEW開發自動駕駛的雙目測距系統
雙目測寬儀高質量生產利器 測寬儀價格
AD1955在處于DSD模式時只能是stereo嗎?
機器視覺雙目測寬儀具體有什么優勢?
雙目影像密集匹配算法的綜合分析





 雙目視覺經典視差優化算法:Fast Bilateral-Space Stereo
雙目視覺經典視差優化算法:Fast Bilateral-Space Stereo










評論