異或門,英文名Exclusive OR Gate,簡稱為XOR Gate,它是一種重要的數(shù)字邏輯門,可以實現(xiàn)異或邏輯,即當(dāng)且僅當(dāng)其中一個輸入為高時,輸出為高。如果兩個輸入均為低或高,則輸出為低。
符號
眾所周知,定義電子元件有多種標(biāo)準(zhǔn)。通常情況下,一般會遵循 IEEE(電氣和電子工程師協(xié)會)和 IEC(國際電工委員會)標(biāo)準(zhǔn)。在IEEE和IEC標(biāo)準(zhǔn)中,異或門邏輯符號如下所示:
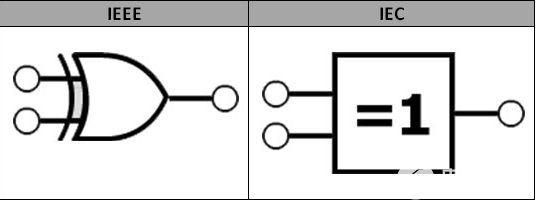
異或門的布爾表達式不能像AND、OR門一樣直接確定。由于異或門是一個混合門,因此異或門的輸出的布爾表達式由輸入的乘法、加法和反相的組合給出。因此,必須使用卡諾圖(K-Maps)以及真值表來推導(dǎo)XOR門的布爾表達式。
真值表
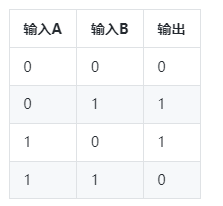
異或門的真值表如下表格所示。由此可以清楚地看出,當(dāng)兩個輸入相同時,異或門會在其輸出端產(chǎn)生邏輯低電平(即邏輯“0”)(兩者都可能為低電平或兩者都可能為高電平)。
低邏輯,在其輸出端即邏輯“0”。當(dāng)兩個輸入不同時,在其輸出端產(chǎn)生邏輯高值,即邏輯“1”。
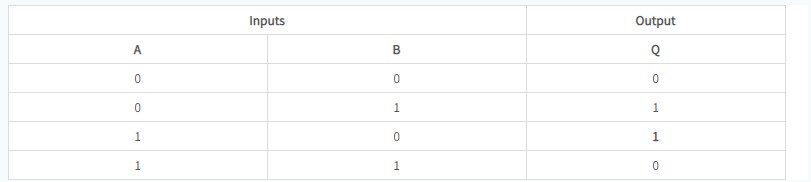
上述異或門真值表的K-map表示如下圖所示:
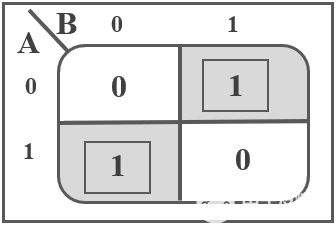
布爾表達式
使用上面的真值表和對應(yīng)的K-Map,現(xiàn)在可以推導(dǎo)出XOR Gate的布爾表達式。如果A和B是XOR門的輸入,則其輸出為:A▔B + AB▔。
XOR輸出表示為:A⊕B ,也可以寫成:(A + B) ( A▔+ B▔ ) 。
通過應(yīng)用德摩根定律,上述布爾表達式也可以寫成: (A + B) (A▔B▔) 。
等效電路
異或門定義為具有2個輸入以執(zhí)行異或運算的混合邏輯門。從以上計算公式可知,異或門的主要布爾表達式為:A▔B + AB▔。
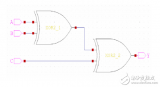
因此,具有2個輸入的XOR電路是使用AND、OR和NOT門門設(shè)計的,如下圖所示:
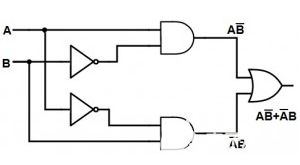
2輸入異或門的輸出只有當(dāng)其輸入之一為高時才為高電平。如果兩個輸入相同,則輸出為低電平。
使用基本邏輯門的異或門
如果一個特定的門不能直接使用,那么可以使用多個門來設(shè)計XOR Gate。異或門可以通過使用NAND門和NOR門等基本邏輯門來設(shè)計,因為它們是通用門。
1、或非門
現(xiàn)在來看看如何使用或非門實現(xiàn)XOR Gate。為此,必須重寫上面的XOR布爾方程。
Q=A▔B + AB▔
Q = A▔B + AB▔ + AA▔ + BB▔
Q = ( A▔ + B▔ ) (A + B)
Q = ( A▔ + B▔ ) (A + B) = (A' + B') (A + B)
兩邊取補,得到:
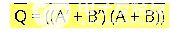
使用德摩根定律,可以得到:
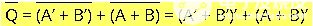
再次對兩邊取補,最終得到:
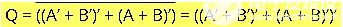
這個等式看起來可以使用或非門來實現(xiàn)。總共需要五個或非門(兩個用于反相A和B,一個用于A和B的NOR,一個用于A'和B' 的NOR,最后一個用于獲得上述等式)。下圖顯示了使用或非門實現(xiàn)的XOR Gate。
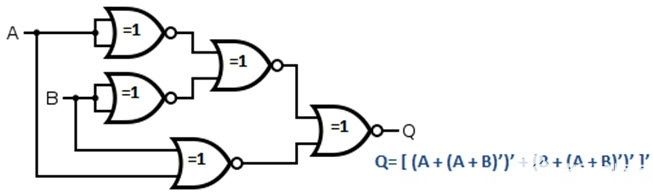
2、與非門
接下來看看如何使用與非門實現(xiàn)XOR Gate。為此,繼續(xù)重寫上面的XOR布爾方程。
Q = A▔B + AB▔
Q = A▔B + AB▔ + AA▔ + BB▔
Q = (A + B) ( A▔ + B▔ )
Q = (A + B) ( A▔ + B▔ ) = (A + B) (A' + B')
將德摩根定律應(yīng)用于上述等式的第二項,可以得到:
Q = (A + B) ( A▔B▔ )
現(xiàn)在需要使用與非門來實現(xiàn)這個電路,即有:
Q = A ( A▔B▔ ) + B ( A▔B▔ ) = A (AB)' + B (AB)'
兩邊取補,得到:
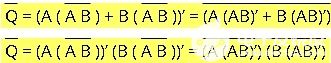
最后,再次在兩邊應(yīng)用補碼,得到:
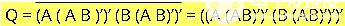
這個等式現(xiàn)在就可以使用與非門來實現(xiàn),這里主要使用與非門就可以了。下圖顯示了使用與非門實現(xiàn)的XOR Gate:
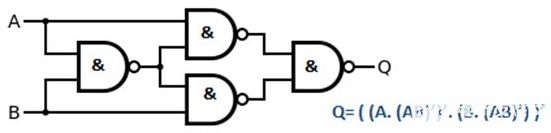
3、使用與門、或門和與非門
現(xiàn)在來看看如何使用NAND、AND和OR門來實現(xiàn)XOR門。為此,仍然需要重寫上面的XOR布爾方程。
Q = A▔B + AB▔
Q = A▔B + AB▔ + AA▔+ BB▔
Q = (A + B) ( A▔ + B▔ )
Q = (A + B) ( A▔ + B▔ ) = (A + B) (A' + B')
將德摩根定律應(yīng)用于上述等式的第二項,可以得到:
Q = (A + B) ( A▔B▔ )
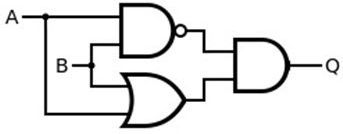
上述等式中的第一項需要一個或門,第二項需要一個與非門,最終等式可以使用與門獲得,如下圖所示:
脈沖操作
2輸入異或門的脈沖操作如下圖所示:
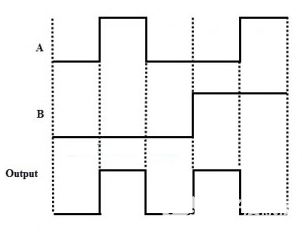
3輸入異或門
在某些情況下,需要有超過2個輸入的異或門。超過2個輸入XOR函數(shù)稱為“奇數(shù)函數(shù)”或者“模2和數(shù)(Modulo-2 sum)”。3輸入XOR門的布爾函數(shù)為:Q = A ⊕ B ⊕ C = A▔B▔C + A▔BC▔+ AB▔C▔+ ABC。
下面給出了三輸入異或門邏輯符號:
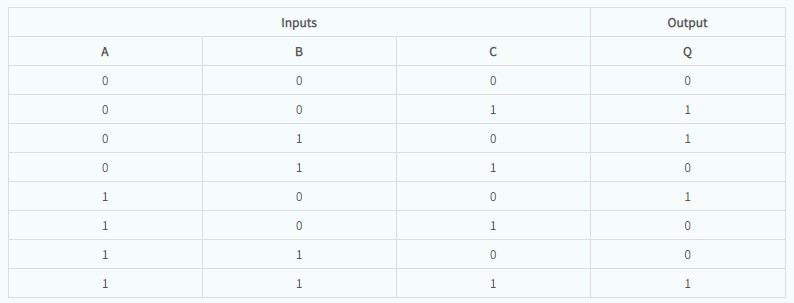
3輸入異或門真值表
對于3輸入XOR門,當(dāng)奇數(shù)輸入處于高電平時,則具有高輸入。因此,3輸入異或門被稱為“奇數(shù)功能或門”。
常用的TTL和CMOS邏輯異或門IC
以下是一些常用的XOR IC 的列表,僅供參考:
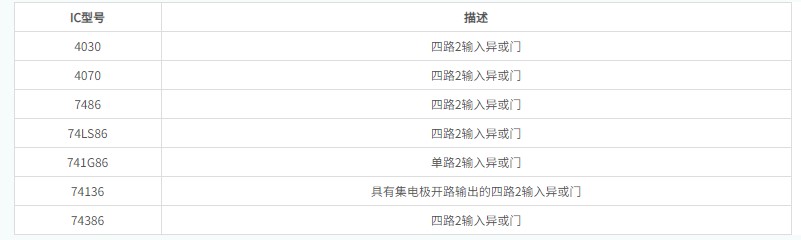
其中,最流行的基于TTL邏輯的異或門IC是74LS86,它是一款四路2輸入異或IC。而對于基于CMOS邏輯的異或門IC,CD4030四路2輸入異或門IC是一種主流的選擇。
7486四路2輸入異或門IC
IC 7486是一個四路2輸入異或門,即它在一個封裝中包含四個2輸入異或門,其管腳圖和管腳描述如下所示:
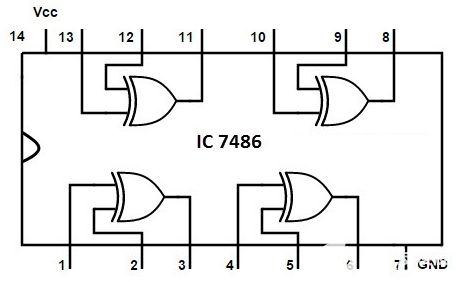
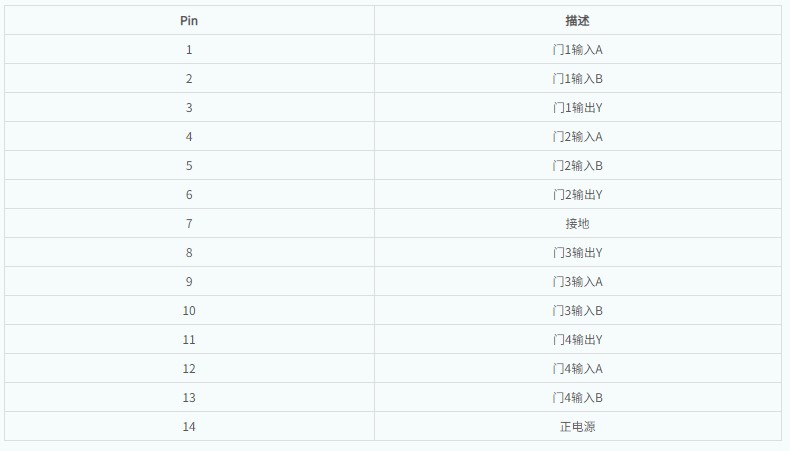
主要應(yīng)用
1、用于加法器
可以設(shè)計一位加法器(也稱為半加法器),它將添加兩位并產(chǎn)生一位輸出。使用異或門設(shè)計的單位加法器如下圖所示:
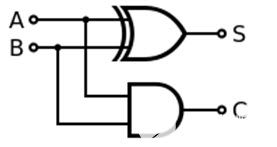
如果在二進制加法中將“1”和“1”兩個位相加,得到答案“10”,在十進制加法中得到 2。半加法器的主要原理是通過“異或”門的輸出實現(xiàn)尾隨和,并通過“與”門計算進位。
其實,可以級聯(lián)多個單位加法器電路以形成n位加法電路,從而計算較長二進制數(shù)的和。
2、偽隨機數(shù)生成
線性移位寄存器也稱為偽隨機數(shù)發(fā)生器 (PNR)。為了產(chǎn)生隨機數(shù),可以通過形成一個線性反饋移位寄存器以特定順序排列XOR邏輯門。
3、相關(guān)和序列檢測
當(dāng)所有輸入為高或低時,異或門能夠產(chǎn)生低電平輸入,即0。當(dāng)在長數(shù)據(jù)序列中搜索特定位序列時,可以使用XOR門來找到所需的數(shù)據(jù)位序列。
在目標(biāo)序列中找到所需的數(shù)據(jù)位串的準(zhǔn)確性是通過計算獲得的0的數(shù)量來確定的。在許多通信設(shè)備(如解碼器和CDMA接收機)中,一般使用相關(guān)器,用于提取一組PRN序列中特定偽隨機數(shù)序列的奇偶校驗。
總結(jié)
以上就是異或門(XOR Gate)的相關(guān)基礎(chǔ)內(nèi)容,主要包括XOR Gate的符號、真值表和布爾表達式。與此同時,還介紹了使用NOR和NAND門實現(xiàn)XOR Gate,以及一些常見主流的XOR IC,希望上述內(nèi)容能夠?qū)Υ蠹矣兴鶐椭?/p>
-
邏輯門
+關(guān)注
關(guān)注
1文章
136瀏覽量
23971 -
異或門
+關(guān)注
關(guān)注
1文章
31瀏覽量
17750 -
與非門
+關(guān)注
關(guān)注
1文章
120瀏覽量
12645
發(fā)布評論請先 登錄
相關(guān)推薦
XOR自門控與時鐘門控的不同之處
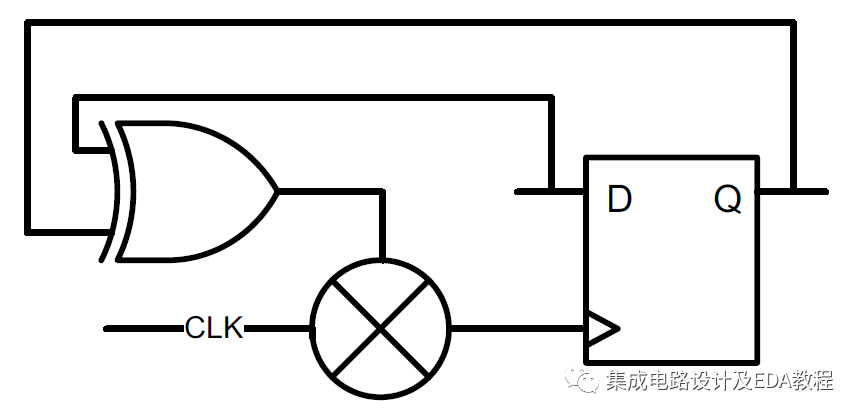
如何確定芯片的方向 最簡單的芯片原理
labview基礎(chǔ)知識
通信基礎(chǔ)知識教程
什么是XOR
使用Eclipse基礎(chǔ)知識
電源管理基礎(chǔ)知識電源管理基礎(chǔ)知識電源管理基礎(chǔ)知識
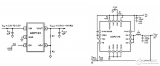
異或門的電路符號表達_XOR的電路實現(xiàn)





 異或門(XOR Gate)的基礎(chǔ)知識
異或門(XOR Gate)的基礎(chǔ)知識
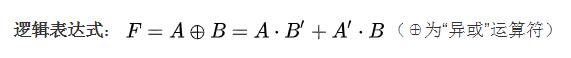
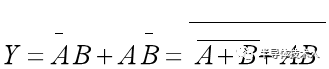










評論