電壓反饋型運算放大器的增益和寬帶

簡介

本文考察標定運算放大器的增益和寬帶的常用方法。需要指出的是，適用于電壓反饋(VFB)型運算放大器。

開環增益

與理想的運算放大器不同，實際的運算放大器增益是有限的。開環直流增益(通常表示為AVOL)指放大器在反饋環路未閉合時的增益，因而有了“開環”之稱。對于精密運算放大器，該增益可能非常高，為160 dB(1億)或以上。從直流到主導極點轉折頻率，該增益表現平坦。

此后，增益以6 dB/8倍頻程(20 dB/10倍頻程)下降。(8倍頻程指頻率增加一倍，10倍頻程指頻率增加十倍。)如果運算放大器有一個單極點，則開環增益繼續以該速率下降，如圖1A所示。實際的運算放大器一般有一個以上的極點，如圖1B所示。第二個極點會使開環增益下降至12 dB/8倍頻程(40 dB/10倍頻程)的速率增加一倍。如果開環增益在達到第二個極點的頻率之前降至0 dB(單位增益)以下，則運算放大器在任何增益下均會無條件地保持穩定。數據手冊上一般將這種情況稱為單位增益穩定。如果達到第二個極點的頻率且閉環增益大于1 (0 db)，則放大器可能不穩定。有些運算放大器設計為只有在較高閉環增益下才保持穩定，這就是所謂的非完全補償運算放大器。

然而，運算放大器可能在較高頻率下擁有更多額外的寄生極點，前兩個極點一般都是最重要的。

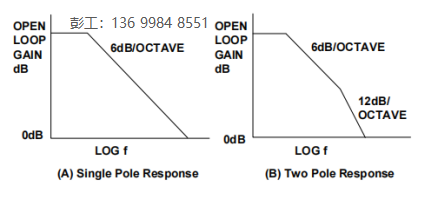
圖1：開環增益(波特圖) (A) 單極點響應、(B)雙極點響應

有必要了解開環增益、閉環增益、環路增益、信號增益和噪聲增益之間的區別。它們性質類似、相互關聯，但也存在差異。下面我們將詳細討論。

開環增益并不是一項精確控制的參數。其范圍相對較大，在規格參數中，多數情況下均表示為典型值而非最小/最大值。有些情況下，一般指高精度運算放大器，該參數會有一個最小值。

另外，開環增益可能因輸出電壓電平和負載而變化。這就是所謂的開環增益非線性度。該參數與溫度也有一定的相關性。一般來說，這些影響很小，多數情況下都可以忽略不計。事實上，一些運算放大器的數據手冊中未必包含開環增益非線性度。

閉環增益

閉環增益指放大器在反饋環路閉合時的增益，與其相反，開環增益則是放大器在反饋環路斷開時的增益。閉環增益有兩種形式：信號增益和噪聲增益。下面對兩者進行說明并加以區分。

閉環放大器增益的經典表達式涉及開環增益。設G為實際閉環增益，NG 為噪聲增益(見下文)，AVOL 為放大器的開環增益，

則：

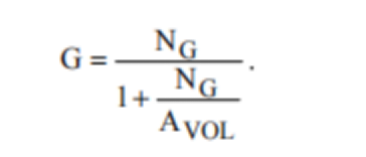
顯然，如果開環增益很高，一般情況下都是如此，則電路的閉環增益就是噪聲增益。

信號增益與噪聲增益

信號增益指連接反饋環路時施加于輸入信號的增益。討論了反相和同相電路的增益，更確切地說，實際上就是閉環信號增益。信號增益可為正(同相模式)，也可為負(反相模式)，反相模式下，可能低于單位增益。信號增益是在設計信號路徑

元件時最重要的增益。圖2詳細展示了各種增益的情況。

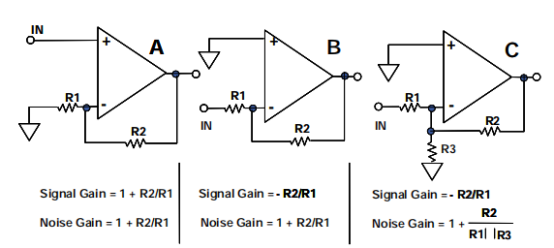
圖2：信號增益與噪聲增益

放大器放的電壓噪聲和偏移電壓反射到通過噪聲增益進行輸出。

放大放的電壓噪聲和偏移電壓反射到通過噪聲增益進行輸出。

電路C的信號增益不變，但噪聲增益越高，因此穩定性越好，噪聲越差，輸出偏移電壓越高。

反相放大器級的信號增益為：

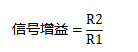
同相放大器則為：

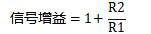
噪聲增益指出現在與運算放大器輸入端串聯的噪聲源(輸入電壓噪聲)或電壓源(輸入失調電壓)上的增益。噪聲增益等于:

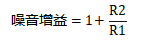
噪聲增益等于同相放大器的信號增益。同時，反相級或同相級的噪聲增益是相同的。

用于確定運算放大器穩定性的是噪聲增益。噪聲增益等于波特圖中用到的閉環增益。上面的噪聲增益表達式中用到電阻值，但是，在實際應用中，它們實際上是帶有實部和虛部的阻抗。

環路增益

開環增益與閉環增益之差稱為環路增益，如圖3所示。環路增益給出了可以在給定頻率下施加于放大器的負反饋量。

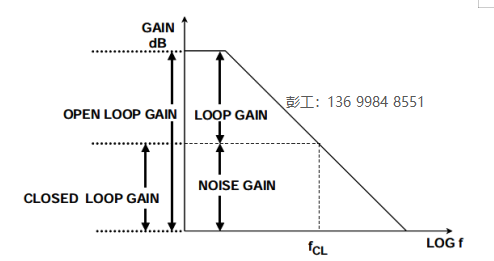
圖3：增益定義

波特圖：漸近和實際響應

基于對數-對數比例的開環增益與頻率的關系坐標圖稱為波特圖。這是評估某個運算放大器是否適合特定應用的主要工具之一。

如果在波特圖上先畫上開環增益，然后繪出噪聲增益(如圖4所示)，則其交點將決定放大器系統的最大閉環帶寬。該交點通常被稱為閉環頻率(FCL)。請記住，交點處的實際響應值比該值低3 dB。在比FCL高和低一個8倍頻程的頻率下，漸近響應與實際響應之差將小于1 dB。

波特圖也可用于確定穩定性。如上所述，如果閉環增益(噪聲增益)在大于6 dB/8倍頻程(20 dB/10倍頻程)的斜率下與開環增益相交，則放大器可能不穩定(取決于相位余量)。

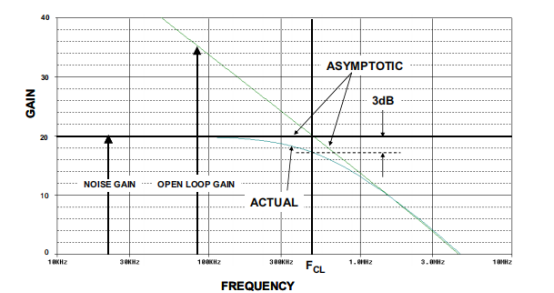
圖4：波特圖——漸近響應與實際響應

增益帶寬積

對于單極點響應，開環增益以6 dB/8倍頻程下降。這就是說，如果我們將頻率增加一倍，增益會下降兩倍。相反，如果使頻率減半，則開環增益會增加一倍，如圖5所示。結果產生所謂的增益帶寬積。如果用頻率乘以開環增益，其積始終為一個常數。需要注意的是，必須處于整條曲線中以6 dB/8倍頻程下降的部分。這樣，我們就得到了一個品質因素，可以據此決定某個運算放大器是否適合特定的應用。請注意，增益帶寬積僅對電壓反饋(VFB)運算放大器有意義。

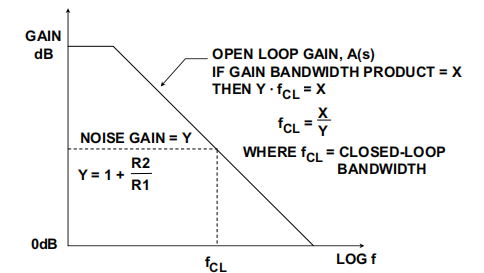
圖5：增益帶寬積

例如，如果有這樣一個應用，要求閉環增益為10，帶寬為100 kHz，則需要一個最低增益帶寬積為1 MHz的運算放大器。但這有點把問題過度簡單化了，因為增益帶寬積變化極大，而且在閉環增益與開環增益相交的位置，響應實際上要低3 dB。另外，還應該允許一定的額外余量。

在上述應用中，增益帶寬積為1 MHz的運算放大器是最低要求。保險起見，為了實現要求的性能，因數至少應該是5。因此選擇了增益帶寬積為5 MHz的運算放大器。

穩定性標準

反饋穩定性理論認為，閉環增益必須在不大于6 dB/8倍頻程(單極點響應)的斜率下與開環增益相交，才能使系統實現無條件穩定。如果響應為12 dB/8倍頻程(雙極點響應)，則運算放大器會發生振蕩。簡單起見，不妨這樣設想，每個極點增加90°相移。兩個極點則會產生180°的相移，而180°的相移會使負反饋變成正反饋，即振蕩。

那么問題是：為什么要用單位增益下不穩定的放大器呢?答案是，對于給定的放大器，如果該放大器設計時未考慮單位增益穩定性，則可在較高增益下提高帶寬。這類運算放大器有時被稱為非完全補償運算放大器。然而，仍需滿足穩定性標準，即閉環增益必須在6dB/8倍頻程(單極點響應)的斜率下與開環增益相交。否則，放大器將會振蕩。因此，非完全補償運算放大器僅在數據手冊中規定的較高增益下保持穩定。

舉例來說，不妨比較圖6中的開環增益圖。圖中的三種器件，AD847、AD848 和 AD849基本上采用相同的設計，只是內部補償機制不同。AD847為單位增益穩定型，規定增益帶寬為50 MHz。AD848在增益為5或以上時保持穩定，其增益帶寬為175 MHz。AD849在增益為25或以上時保持穩定，其增益帶寬為725 MHz。由此可見，在基本設計相同的情況下，可以通過修改運算放大器的內部補償機制來產生不同的增益帶寬積，其為最低穩定增益的函數。

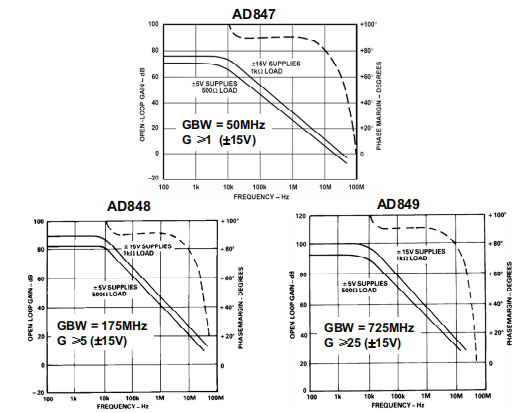
圖6：AD847、AD848、AD849的開環增益特性、增益帶寬積和最低穩定閉環增益

相位余量

衡量穩定性的一項指標是相位余量。正如幅度響應不會一直保持平坦卻突然變化一樣，相位響應也會從轉折頻率前的大約十倍頻程開始逐漸變化。相位余量指在達到180°之前剩余的相移量，在閉環增益與開環增益相交的頻率下進行測量。

低相位余量造成的結果是，增益峰值會剛好在閉環增益與開環增益的相交頻率之前增加。圖7顯示了AD8051運算放大器的增益和相位響應。這種情況下，相位余量與單位增益頻率成45°。

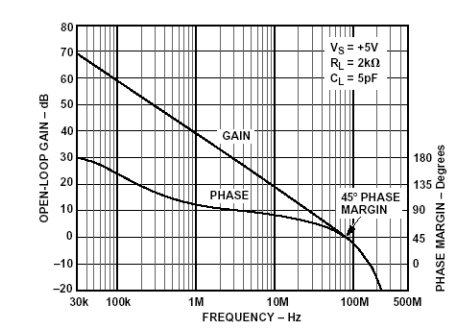
圖7：AD8051相位余量